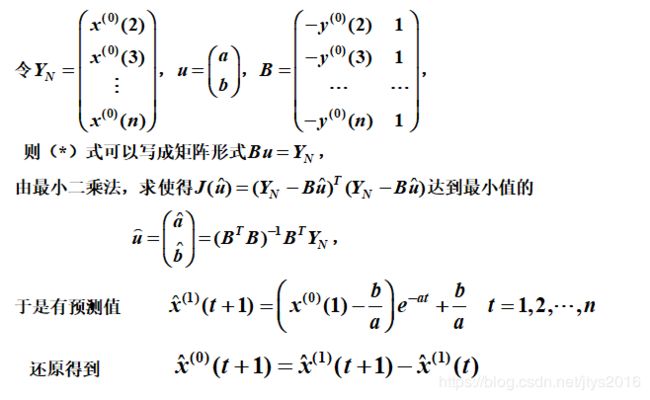数学建模之灰色预测实例含代码

参考书籍《数学建模算法与应用》

一，预备

（1）原理

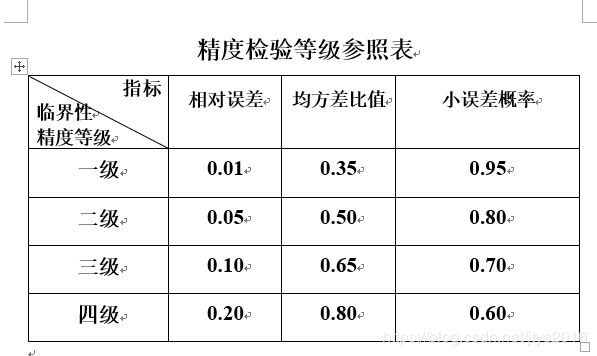
（2）精度表

 

二， 灰色预测的步骤

 北方某城市 1986～1992 年道路交通噪声平均声级数据见表1

表1 市近年来交通噪声数据[dB(A)]

序号	年份		序号	年份
1	1986	71.1	5	2000	71.4
2	1987	72.4	6	2001	72.0
3	1988	72.4	7	2002	71.6
4	1999	72.1

（1）级比检验

（2）GM(1,1)建模

(4)模型检验

GM(1,1)检验表

序号	年份	原始值	模型值	C(均方差比值)	P(小误差概率)	精度等级
1	1986	71.1	71.1	0.2311	0.8571	二级
2	1987	72.4	72.4057
3	1988	72.4	72.2362
4	1989	72.1	72.0671
5	1990	71.4	71.8984
6	1991	72.0	71.7301
7	1992	71.6	71.5622

书籍上代码运行有误，参考其他代码，地址为https://www.cnblogs.com/manhua/p/5510105.html

三，代码

clear
syms t
X0 = input('请输入原始数据：');   %输入原始数据
n = length(X0);  %原始n年数据
lamda=X0(1:n-1)./X0(2:n) %计算级比 
range=minmax(lamda)  %计算级比的范围,在exp(-2/(n-1))~exp(2/(n+2))范围则可以进行灰色预测

%累加生成
X1 = zeros(1,n);
for i = 1:n
    if i == 1
        X1(1,i) = X0(1,i);
    else
        X1(1,i) = X0(1,i) + X1(1,i-1);
    end
end
X1

%计算数据矩阵B和数据向量Y
B = zeros(n-1,2);
Y = zeros(n-1,1);
for i = 1:n-1
    B(i,1) = -0.5*(X1(1,i) + X1(1,i+1));
    B(i,2) = 1;
    Y(i,1) = X0(1,i+1);
end
B,Y

%计算GM(1,1)微分方程的参数a和u
u = zeros(2,1);
u = inv(B'*B)*B'*Y;
a = u(1,1);
b = u(2,1);
a,b  

%建立灰色预测模型 XX0
XX0(1,1) = X0(1,1);
for i = 2:n
    XX0(1,i) = (X0(1,1) - b/a)*(1-exp(a))*exp(-a*(i-1));
end
XX1=vpa((X0(1,1) - b/a)*exp(-a*t)+b/a,6) %这是累加后的预测值，例如t=2时，XX1则是T=1和T=2预测结果的累加值，XX0不是累加
XX0

%模型精度的后验差检验
e = 0;          %求残差平均值
for i =1:n
    e = e + (X0(1,i) - XX0(1,i));
end
e = e/n;
e
aver = 0;       %求历史数据平均值
for i = 1:n
    aver = aver + X0(1,i);
end
aver = aver / n;
aver
s12 = 0;      %求历史数据方差
for i = 1:n
    s12 = s12 + (X0(1,i)-aver)^2;
end
s12 = s12 / n;
s12
s22 = 0;       %求残差方差
for i = 1:n
    s22 = s22 + ((X0(1,i) - XX0(1,i)) - e)^2;
end
s22 = s22 / n;
s22
C = s22 / s12;    %求后验差比值(C为均方差比值)
C
cout = 0;    
for i = 1:n
    if abs((X0(1,i) - XX0(1,i)) - e) < 0.6754*sqrt(s12)
        cout = cout+1;
    else
        cout = cout;
    end
end
P = cout / n; %P为小误差概率
P
if (C < 0.35 & P > 0.95)   %可修改，修改成二级，三级，对照预备中的表
    disp('预测精度为一级');
   m = input('请输入需要预测的年数: m = ');   %预测往后各年的负荷
    disp('往后m各年负荷为：');
    f = zeros(1,m);
    for i = 1:m
        f(1,i) = (X0(1,1) - b/a)*(1-exp(a))*exp(-a*(i+n-1));
    end
    f
else
    disp('未达到一级精度');
end

三，结果

（1）级比

（2）计算a,b和预测值,a=u(1),b=u(2)

(3)预测值

（4）检验值及结果

1993,1994,1995的预测值分别为71.3946，71.2275，71.0608.