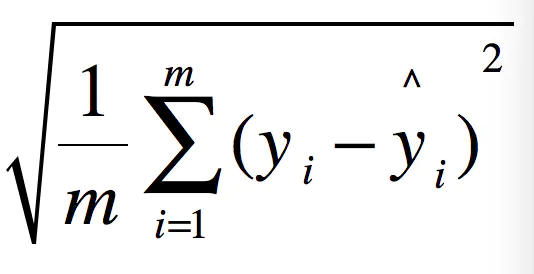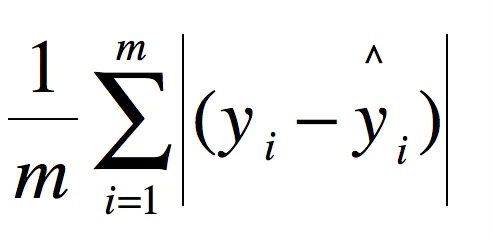关于各种回归评价指标MSE、RMSE、MAE、R-Squared、Standard Deviation(标准差)
分类问题的评价指标是准确率,那么回归算法的评价指标就是MSE,RMSE,MAE、R-Squared。下面一一介绍:
1、均方误差(MSE)
MSE (Mean Squared Error)叫做均方误差,是反映估计量与被估计量之间差异程度的一种度量。设t是根据子样确定的总体参数θ的一个估计量,(θ-t)2的数学期望,称为估计量t的均方误差。它等于σ2+b2,其中σ2与b分别是t的方差与偏倚。MSE=
用 真实值-预测值 然后平方之后求和平均。在线性回归的时候我们的目的就是让这个损失函数最小。
2、均方根误差(RMSE)
RMSE(Root Mean Squard Error)均方根误差,亦称标准误差,其定义为 ,i=1,2,3,…n。在有限测量次数中,均方根误差常用下式表示:√[∑di^2/n]=Re,式中:n为测量次数;di为一组测量值与真值的偏差。如果误差统计分布是正态分布,那么随机误差落在±σ以内的概率为68%。RMSE=
这不就是MSE开个根号么。有意义么?其实实质是一样的。只不过用于数据更好的描述。
例如:要做房价预测,每平方是万元(真贵),我们预测结果也是万元。那么差值的平方单位应该是 千万级别的。那我们不太好描述自己做的模型效果。怎么说呢?我们的模型误差是 多少千万?。。。。。。于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的可,在描述模型的时候就说,我们模型的误差是多少万元。
3、MAE
平均绝对误差(Mean Absolute Deviation),又叫平均绝对离差,是所有单个观测值与算术平均值的偏差的绝对值的平均。平均绝对误差可以避免误差相互抵消的问题,因而可以准确反映实际预测误差的大小。MAE=
4、R-Squared
R平方(R-squared)是反映业绩基准的变动对基金表现的影响,影响程度以 0~100 计。如果R平方值等于100,表示基金回报的变动完全由业绩基准的变动所致;若R平方值等于35,即35%的基金回报可归因于业绩基准的变动。简言之,R 平方值越低,由业绩基准变动导致的基金业绩的变动便越少。此外,R平方也可用来确定β系数或α系数的准确性。一般而言,基金的R平方值越高,其两个系数的准确性便越高。
上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价 那么误差单位就是万元。数子可能是3,4,5之类的。那么预测身高就可能是0.1,0.6之类的。没有什么可读性,到底多少才算好呢?不知道,那要根据模型的应用场景来。
看看分类算法的衡量标准就是正确率,而正确率又在0~1之间,最高百分之百。最低0。很直观,而且不同模型一样的。那么线性回归有没有这样的衡量标准呢?答案是有的。
那就是R Squared也就R方
光看这些东西很懵逼,其中分子是Residual Sum of Squares 分母是 Total Sum of Squares,公式=
慢慢解释。其实这个很简单。上面分子就是我们训练出的模型预测的所有误差,下面分母就是不管什么我们猜的结果就是y的平均数。
那结果就来了。
如果结果是0,就说明我们的模型跟瞎猜差不多。
如果结果是1。就说明我们模型无错误。
如果结果是0-1之间的数,就是我们模型的好坏程度。
如果结果是负数。说明我们的模型还不如瞎猜。(其实导致这种情况说明我们的数据其实没有啥线性关系)
化简上面的公式
分子分母同时除以m
那么分子就变成了我们的均方误差MSE,下面分母就变成了方差。
5、标准差
标准差(Standard Deviation),中文环境中又常称均方差,是离均差平方的算术平均数的平方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
![]()
均方根误差RMSE是观测值与真值偏差的平方与观测次数n比值的平方根,在实际测量中,观测次数n总是有限的,真值只能用最可信赖(最佳)值来代替.标准误差 对一组测量中的特大或特小误差反映非常敏感,所以,标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。因此,标准差是用来衡量一组数自身的离散程度,而均方根误差是用来衡量观测值同真值之间的偏差,它们的研究对象和研究目的不同,但是计算过程类似.
6、代码
MSE
y_preditc=reg.predict(x_test) #reg是训练好的模型
mse_test=np.sum((y_preditc-y_test)**2)/len(y_test) #跟数学公式一样的
RMSE
rmse_test=mse_test ** 0.5
MAE
mae_test=np.sum(np.absolute(y_preditc-y_test))/len(y_test)
R-Squared
1- mean_squared_error(y_test,y_preditc)/ np.var(y_test)
scikit-learn中的各种衡量指标
from sklearn.metrics import mean_squared_error #均方误差
from sklearn.metrics import mean_absolute_error #平方绝对误差
from sklearn.metrics import r2_score#R square
#调用
mean_squared_error(y_test,y_predict)
mean_absolute_error(y_test,y_predict)
r2_score(y_test,y_predict)