一篇文章完全弄懂线性回归（Linear Regression）（含详细推导以及代码）

个人的原创笔记，欢迎dalao们指正错误！

---

线性回归（Linear Regression）

什么是回归分析？

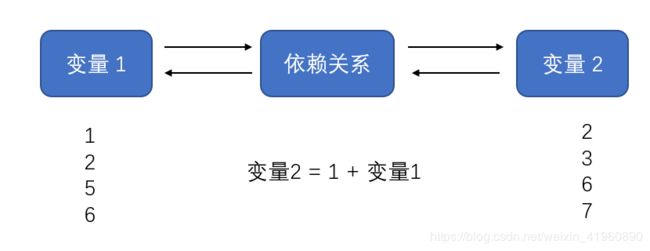
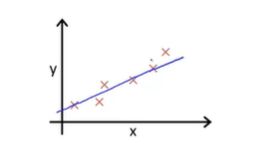
回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。下图是两个变量之间的关系图：

也就是用数学语言表达变量之间的关系。举个例子：

---

什么是线性回归？

线性回归就是变量之间的相互依赖关系可以通过一个线性方程表达。

这里借用吴恩达老师经典的例子。在房价预测中，假设房价仅由房子的面积大小决定，也就是房价“依赖”与房子的面积。此时我们可以设房价为因变量，记为  ，房子的面积为自变量，记为  ，建立一个单变量线性方程来表述这个依赖关系，记为 。列出方程如下：

我们根据已有的样本对模型训练，就可以得到对应  和  的取值。当我们完成训练时，我们就已经得到一个房价关于房子面积的准确的表达式，通过此式，我们可以使用一个房子的面积来估计其价格（估计而不是确定，因为存在误差）。

整个过程就是单变量线性回归的完整过程。

我们通常把  和  成为模型的参数，对模型的训练过程就是对模型参数的求解过程。一旦确定了  和  ，模型就确定下来了。

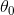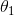如何确定  和 ？

  和  是模型的参数，反映  与  之间的关系。由于样本分布不总是规律的（总有一些点是无法被  覆盖），因此，我们希望模型尽可能地贴近训练样本。这个贴近样本分布的过程，我们称之为拟合。

那么下面要解决的问题就是，我们如何保证计算出来的  足够拟合样本？很简单，使用他们之间的距离来表达差异程度即可。

这个式子又称为代价函数（cost function）。解释一下：

1. 求和：因为是考虑所有样本的距离，因此需要对所有的距离求和。
2. 除以 ： 在这里是样本容量。除以  也就是对其求平均值。（整体的视角）
3. 平方：为了消除正负号（有的样本在直线上侧，有的在直线的下测）。
4. 除以 2：在后面推导 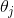 时就会发现，平方求导出来的2正好能抵消。

距离描述：真实值与预测值的差的平方和。我们希望这距离越小，越能拟合样本，使模型更好地表达，因此我们可以顺理成章地得出线性回归的目标： ，也就是最小化代价函数。

那么下面要解决的问题就是，怎么最小化代价函数？

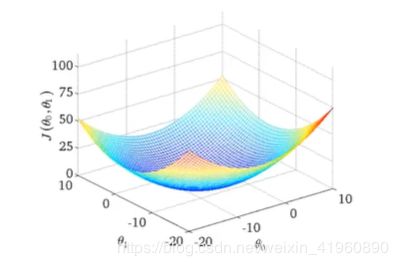
我们根据  表达式可以画出如下的图：

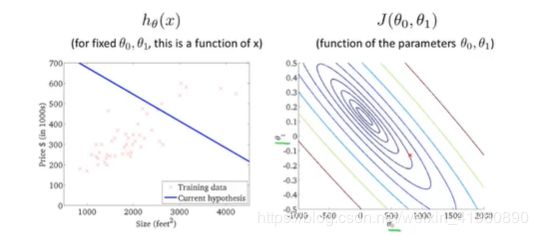
将其三维图像映射到二维，使用等高线图表示如下：

很显然，我们发现，求 ，也就是求  取全局最小值时的  和  。

计算全局最小值，我们采用梯度下降法。

怎么使用梯度下降法？

何为梯度下降？我们可以将下降理解为“从山顶上下山的过程”，如何下山能最快到达山底呢？沿着最陡峭的坡滚下去！这里最陡的坡的方向就是我们的梯度的方向。方向我们已经选取好了，就是我们的梯度下降的方向。那么在梯度方向上我们每一步走多远呢？这就是通过步长来决定，也称学习率，记作 。

那么综合了方向和步长，我们可以列出  和  的更新公式如下：

于是，我们可以随机设置初始  和  ，然后根据上述公式开始迭代，当  和  的值不再更新为迭代停止的标志。

这里的  的选择对结果以及训练时间是有很大影响，过小的步长会导致学习速度较慢，增加迭代次数或者有可能导致陷入局部最优解；而过大的步长可能会出现难以收敛的情况。这方面我会在别的笔记中补充。因此，选择一个适当的  是很重要的。

那么这里我将详细地对线性回归的梯度下降进行推算：

注意：   是因为平方项求导出来会产生一个2，相互抵销了。  的求导由于前面有系数  ，因此在表达式后面乘了  。如果还是不懂的话，建议百度一下复合函数求导。

补充：近期在手推模型，感兴趣的可以看看：

【线性回归】正规方程+梯度下降+正则化完整推导！

代码实现

主要就是跟着公式般下来。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

train = pd.read_csv('Salary_Data.csv')
train.size

输出：60

x = train.iloc[:,0].values
y = train.iloc[:,-1].values
x_ = train.iloc[:,0].values
y_ = train.iloc[:,-1].values
theta_0 = 1
theta_1 = 1
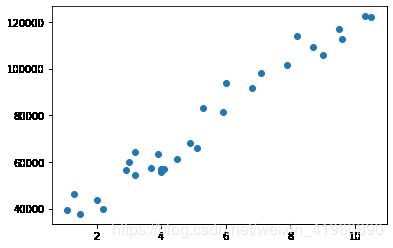
alpha = 0.01

plt.scatter(x, y)
plt.show()

输出：

自己实现线性回归

## H函数
def hF(x, theta0, theta1):
    return theta0 + theta1 * x;
##梯度下降过程
def GD_step1(theta_0, theta_1):
    sum = 0
    for index in range(x.size):
       sum += hF(x[index], theta_0, theta_1) - y[index]
    return sum
def GD_step2(theta_0, theta_1):
    sum = 0
    for index in range(x.size):
       sum += (hF(x[index], theta_0, theta_1) - y[index]) * x[index]
    return sum
## 梯度下降     
def GD_0(theta_0, theta_1):
    for a in range(1000):
        for index in range(x.size):
            sum1 = GD_step1(theta_0, theta_1);
            sum2 = GD_step2(theta_0, theta_1);
        theta_0 = theta_0 - alpha *  sum1 / x.size
        theta_1 = theta_1 - alpha *  sum2 / x.size
    return theta_0, theta_1

theta_0, theta_1 = GD_0(theta_0, theta_1)
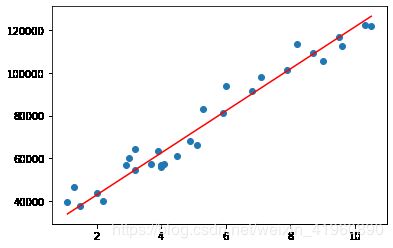
hF(x[0], theta_0, theta_1)

plt.scatter(x, y)
plt.plot(x, hF(x, theta_0, theta_1), c='red')

输出：

调用sklearn

model = LinearRegression()
x_0 = x_.reshape(-1, 1)
y_0 = y_.reshape(-1, 1)
model.fit(x_0, y_0)
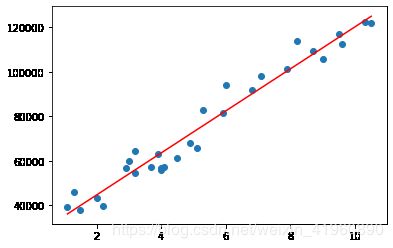
predict = model.predict(x_0)

plt.scatter(x, y)
plt.plot(x, predict, c='red')
plt.show()

 

数据集百度云链接：链接：https://pan.baidu.com/s/1337VuvKHizv8juNMvlWb3Q 提取码：jgb0

代码Github链接：https://github.com/SongJain/MachineLearning/tree/master/LinearRegression