深蓝学院从零开始手写VIO（一）——IMU模型

声明：本专栏文章为深蓝学院《从零开始手写VIO》课程个人学习笔记，更多学习资源请咨询深蓝学院相关课程。

旋转运动学

速度合成公式

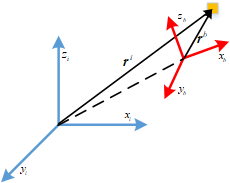
假设有如上图所示的一静一动两个坐标系，按照习惯，我们记动坐标系为体系$\mathbf{b}$，静坐标系为惯性系$\mathbf{i}$。此时有一个物体在空间运动，记其在两个坐标系下的坐标分别为${\mathbf{r}}^i$和${\mathbf{r}}^b$，两者之间的关系为：
$${\mathbf{r}}^i={\mathbf{r}}_{ib}^i+{\mathbf{R}}_{ib}{\mathbf{r}}^b$$
式中上标表示矢量所在的坐标系，${\mathbf{r}}_{ib}^i$表示$\mathbf{b}$系到$\mathbf{i}$系的平移变换矢量，${\mathbf{R}}_{ib}$表示$\mathbf{b}$系到$\mathbf{i}$系的旋转变换矩阵。对上式求解时间导数有：
$$\begin{array}{rl}\frac{d{\mathbf{r}}^i}{dt}& =\frac{d({\mathbf{r}}_{ib}^i+{\mathbf{R}}_{ib}{\mathbf{r}}^b)}{dt}\\ & =\frac{d{\mathbf{r}}_{ib}}{dt}+\frac{d{\mathbf{R}}_{ib}}{dt}{\mathbf{r}}^b+{\mathbf{R}}_{ib}\frac{d{\mathbf{r}}^b}{dt}\\ & ={\mathbf{v}}_{ib}^i+{\mathbf{R}}_{ib}[{\mathbf{\omega }}_{ib}^b{]}_{\times }{\mathbf{r}}^b+{\mathbf{R}}_{ib}{\mathbf{v}}^b\end{array}$$

这里我们引入矢量叉积的一个重要几何性质：
定理1：矢量叉积的旋转不变性。若矩阵$\mathbf{R}$为旋转矩阵，则对于矢量叉积$\mathbf{a}\times \mathbf{b}$有$(\mathbf{R}\mathbf{a})\times (\mathbf{R}\mathbf{b})=\mathbf{R}(\mathbf{a}\times \mathbf{b})$。
利用这一性质，上式可以重写为：
$$\begin{array}{rl}\frac{d{\mathbf{r}}^i}{dt}& ={\mathbf{v}}_{ib}^i+{\mathbf{R}}_{ib}[{\mathbf{\omega }}_{ib}^b{]}_{\times }{\mathbf{r}}^b+{\mathbf{R}}_{ib}{\mathbf{v}}^b\\ & ={\mathbf{v}}_{ib}^i+[{\mathbf{R}}_{ib}{\mathbf{\omega }}_{ib}^b{]}_{\times }[{\mathbf{R}}_{ib}{\mathbf{r}}^b]+{\mathbf{R}}_{ib}{\mathbf{v}}^b\\ {\mathbf{v}}^i& ={\mathbf{v}}_{ib}^i+{\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{R}}_{ib}{\mathbf{v}}^b\end{array}\text{\hspace{1em}(1)}$$

式（1）描述了物体的速度在动坐标系和静坐标系之间的转换关系，又称为速度合成公式或科里奥利方程。由于坐标系原点之间的位移矢量与旋转是相互独立，互不相应的，因此在后续讨论中，我们将省略式（1）中的${\mathbf{v}}_{ib}^i$项，只讨论旋转相关部分。

加速度合成公式

进一步地，我们对式（1）量测继续求时间导数有：
$$\begin{array}{rl}\frac{d{\mathbf{v}}^i}{dt}& =\frac{d({\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i)}{dt}+\frac{d({\mathbf{R}}_{ib}{\mathbf{v}}^b)}{dt}\\ & =\frac{d{\mathbf{\omega }}_{ib}^i}{dt}\times {\mathbf{r}}^i+{\mathbf{\omega }}_{ib}^i\times \frac{d{\mathbf{r}}^i}{dt}+\frac{d{\mathbf{R}}_{ib}}{dt}{\mathbf{v}}^b+{\mathbf{R}}_{ib}\frac{d{\mathbf{v}}^b}{dt}\\ {\mathbf{a}}^i& ={\dot{\mathbf{\omega }}}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{\omega }}_{ib}^i\times {\mathbf{v}}^i+{\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{R}}_{ib}{\mathbf{a}}^b\end{array}$$
将式（1）带入上式有：
$$\begin{array}{rl}{\mathbf{a}}^i& ={\dot{\mathbf{\omega }}}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{\omega }}_{ib}^i\times {\mathbf{v}}^i+{\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{R}}_{ib}{\mathbf{a}}^b\\ & ={\dot{\mathbf{\omega }}}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{\omega }}_{ib}^i\times ({\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{R}}_{ib}{\mathbf{v}}^b)+{\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i+{\mathbf{R}}_{ib}{\mathbf{a}}^b\\ & =\underset{Euler}{{\dot{\mathbf{\omega }}}_{ib}^i\times {\mathbf{r}}^i}+\underset{Centrifugal}{{\mathbf{\omega }}_{ib}^i\times ({\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i)}+\underset{Coriolis}{2{\mathbf{\omega }}_{ib}^i\times {\mathbf{r}}^i}+{\mathbf{R}}_{ib}{\mathbf{a}}^b\end{array}\text{\hspace{1em}(2)}$$
式（2）前三项依次为欧拉力、离心力和科氏力，该式表征了运动物体在静坐标系和动坐标系下的加速度变换关系，称为加速度合成公式。

IMU测量原理

加速度计

单个加速度计的测量原理如上图所示，可以认为是一种弹簧振子模型，对于三轴IMU来说，其内部的三个加速度计正交安装。由于在地面运动的物体处在地球的重力场中，如果我们假设加速度计所在的测量坐标系和当地地理坐标系重合，那么当加速度计静止时，弹簧振子受重力影响，在重力垂线方向的输出并不为零。而是重力矢量$\mathbf{g}$，即：
$$\mathbf{a}=\mathbf{g}=[0,0,-g]$$

陀螺仪

陀螺仪的测量原理包振动陀螺、光纤陀螺、冷原子陀螺等，在低端的MEMS通常采用的为震动陀螺。震动陀螺的本质是通过测量式（2）中Coriolis力${\mathbf{f}}_c=2\mathbf{\omega }\times \mathbf{v}$，进而利用Coriolis力${\mathbf{f}}_c$和线速度$\mathbf{v}$求解出角速度$\mathbf{\omega }$。

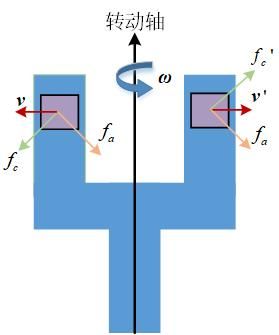
上图为MEMS中所采用的典型音叉振动陀螺的原理图，根据音叉的特性，左右音叉臂上的质量元永远做同速反向振动，此时若音叉以角速度$\mathbf{\omega }$做旋转运动，同时音叉还以外部加速度${\mathbf{f}}_a$运动，将两个音叉的测量量相减可以消去${\mathbf{f}}_a$的影响而只留下由于角运动而产生的科氏力${\mathbf{f}}_a$，最终我们可以得到：
$$2{\mathbf{f}}_a=4\mathbf{\omega }\times \mathbf{v}$$
当然上述假设是在音叉的左右质量元质量完全相等的前提下得到的，在实际应用中，左右质量元不可避免的会存在质量差，从而导致外部加速度引起的力${\mathbf{f}}_a$无法完全消除，这一由外部加速度残差引起的角速度误差的比力称为该陀螺的G-敏感性（G-Sentivity）。

IMU误差模型

IMU传感器的误差主要有确定性误差和随机误差两部分组成，其模型和标定方法如下。

确定性误差

在MEMS IMU传感器中，我们需要考虑的确定性误差主要包括以下三项

• 零偏（Bias）：IMU传感器在完全静止状态下存在的非零输出值，属于加性误差；
• 尺度因子（Scale）： IMU传感器自身尺度不准引起的测量误差，属于乘性误差；
• 不垂直度（Nonorothogonality）：IMU传感器中由于各轴安装不垂直引起的误差，属于乘性误差。

上述三个确定性误差通常可以表示为统一的线性代数形式（矩阵中对角线为尺度因子，其余为不垂直度），以加速度计为例：
$$\left[\begin{array}{c}{a}_x^{\prime }\\ a_y^{\prime }\\ a_z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}{s}_{xx}& m_{xy}& m_{xz}\\ m_{yx}& s_{yy}& s_{yz}\\ m_{zx}& m_{zy}& s_{zz}\end{array}\right]\left[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right]+\left[\begin{array}{c}{b}_{ax}\\ b_{ay}\\ b_{az}\end{array}\right]\text{\hspace{1em}(3)}$$
确定性误差的标定通常采用六面法，即将三轴传感器的分别按照正反轴方向放置（对于加速度计为朝上和朝下，参考值为重力矢量；对于陀螺仪为正转和反转，参考值由标定转台提供），并将测量值带入式（4）中进行最小二乘求解。

此外，温度误差也属于确定性误差，可采用soak或ramp方法标定，这里略过。

随机误差

IMU器件的随机误差主要包括高斯白噪声和随机游走两部分：

• 高斯白噪声：均值为$0$，方差为$\sigma$的独立高斯过程，且该高斯过程的任意两个时刻之间相互独立。
• 随机游走：实习器件中的零偏并不是固定不变的，而是符合维纳过程（wiener process），这使得零偏的导数符合高斯白噪声过程，即：
  $$\dot{\mathbf{b}}(t)={\mathbf{\sigma }}_b\mathbf{w}(t)$$

离散量测下的误差模型

上述误差模型是在连续时间下给出的，而实际器件的量测是离散的，因此需要推导离散时间下的IMU误差模型。按照我们上面给出的误差模型，一个单轴陀螺的量测如下：
$$\begin{array}{rl}\tilde{\omega }(t)& =\omega (t)+b(t)+n(t)\\ \dot{b}(t)& =n_b(t)\end{array}$$

式中$\mathbf{n}(t)$和${\mathbf{n}}_b(t)$均为高斯白噪声。实际传感器的信号采集是通过对一定时间内的信号求平均获得的，因此我们可以假设在信号采集时间内，真实的信号$\mathbf{w}(t)$保持不变，而只有零偏和噪声在变化，即：
$$\tilde{w}(t_0+\Delta t)=w(t_0)+\frac{1}{\Delta t}{\int }_{t_0}^{t_0+\Delta t}[b(t)+n(t)]dt\text{\hspace{1em}(4)}$$
只要知道高斯白噪声和零偏的离散分布即可求得IMU在离散量测下的误差模型，这里我们先看高斯白噪声。

高斯白噪声的离散积分

对于高斯白噪声$\mathbf{n}(t)$来说，根据式（4），其在$\Delta t$时间内的值为：
$$n_d[k]\triangleq n(t_0+\Delta t)=\frac{1}{\Delta t}{\int }_{t_0}^{t_0+\Delta t}n(t)dt$$
由于$n_d[k]$的均值为零，我们可以求解离散情况下$n_d[k]$的方差为：
$$\begin{array}{rl}Var[n_d[k]]& =E[(n_d[k]-E(n_d[k])(n_d[k]-E(n_d[k]){)}^T]\\ & =E[n_d[k{]}^2]\\ & =E\left[\frac{1}{\Delta t^2}{\int }_{t_0}^{t_0+\Delta t}{\int }_{t_0}^{t_0+\Delta t}n(\tau )n(t)d\tau dt\right]\\ & =E\left[\frac{1}{\Delta t^2}{\int }_{t_0}^{t_0+\Delta t}n(\tau )d\tau {\int }_{t_0}^{t_0+\Delta t}n(t)dt\right]\end{array}$$

由在离散条件下，连续积分可以写为有限状态的累加和形式，即：
$$\begin{array}{rl}{\int }_{t_0}^{t_0+\Delta t}n(t)dt& =n(t_0)dt+n(t_0+dt)dt+\cdots +n(t_0+kdt)dt\\ & =\sum _{i=0}^{k}n(t_0+idt)dt\end{array}$$

带入$Var(n_d[k])$的表达式中有：
$$\begin{array}{rl}Var(n_d[k])& =E\left[\frac{1}{\Delta t^2}{\int }_{t_0}^{t_0+\Delta t}n(\tau )d\tau {\int }_{t_0}^{t_0+\Delta t}n(t)dt\right]\\ & =\frac{1}{\Delta t^2}E\left[\sum _{i=0}^{k}n(t_0+id\tau )d\tau \sum _{i=0}^{k}n(t_0+idt)dt\right]\end{array}$$

由于高斯白噪声之间是不相关的，即：
$$E[n(\tau )n(t)]=\{\begin{array}{rl}& {\sigma }_n^2,\tau =t\\ & 0,\tau \ne t\end{array}$$

因此有：
$$\begin{array}{rl}Var[n_d[k]]& =\frac{1}{\Delta t^2}E\left[\sum _{i=0}^{k}n(t_0+id\tau )d\tau \sum _{i=0}^{k}n(t_0+idt)dt\right]\\ & =\frac{{\sigma }_n^2\Delta t}{\Delta t^2}=\frac{{\sigma }_n^2}{\Delta t}\end{array}$$
因此我们可以获得离散状态下的高斯白噪声服从如下分布：
$$n_d[k]\sim N(0,\frac{{\sigma }_n^2}{\Delta t})\text{\hspace{1em}(5)}$$

零偏的离散积分

按照同样的方法，我们现在来看离散状态下的零偏积分方差。首先我们已知零偏的时间导数是一个高斯白噪声$\dot{b}(t)=n_b(t)$，将式（4）中的零偏积分项取出有：
$$\begin{array}{rl}\frac{1}{\Delta t}{\int }_{t_0}^{t_0+\Delta t}b(t)dt& =\frac{1}{\Delta t}{\int }_{t_0}^{t_0+\Delta t}\left(b(t_0)+{\int }_{t_0}^{t_0+\Delta t}{n}_b(\tau )d\tau \right)dt\\ & =\frac{\left(b(t_0)+{\int }_{t_0}^{t_0+\Delta t}{n}_b(\tau )d\tau \right)}{\Delta t}{\int }_{t_0}^{t_0+\Delta t}1dt\\ b(t_0+\Delta t)& =b(t_0)+{\int }_{t_0}^{t_0+\Delta t}{n}_b(\tau )d\tau \end{array}$$

该积分项的期望和方差分别为：
$$\begin{array}{rl}E[b(t_0+\Delta t)]& =E[b(t_0)+{\int }_{t_0}^{t_0+\Delta t}{n}_b(\tau )d\tau ]\\ & =E[b(t_0)]+{\int }_{t_0}^{t_0+\Delta t}E[n_b(\tau )]d\tau \\ & =b(t_0)\\ Var[b(t_0+\Delta t)]& =E\left[(b(t_0+\Delta t)-E[b(t_0+\Delta t)])(b(t_0+\Delta t)-E[b(t_0+\Delta t)]{)}^T\right]\\ & =E\left[{\int }_{t_0}^{t_0+\Delta t}{n}_b(\tau )d\tau {\int }_{t_0}^{t_0+\Delta t}{n}_b(t)dt\right]\\ & =\Delta t{\sigma }_b^2\end{array}$$
因此我们可以获得离散状态下的零偏符合如下分布：
$$b_d[k]\sim N(b_d[k-1],\Delta t{\sigma }_b^2)\text{\hspace{1em}(6)}$$

Allan方差标定

参考以下两个IMU Allan方差标定工具：

• imu_utils
• kalibar_allan

IMU误差的数学模型

在连续时间下，IMU的量测微分方程为：
$$\{\begin{array}{rl}{\dot{\mathbf{p}}}^w& ={\mathbf{v}}^w\\ {\dot{\mathbf{v}}}^w& ={\mathbf{a}}^w\\ {\dot{\mathbf{q}}}_{wb}& ={\mathbf{q}}_{wb}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}{\mathbf{\omega }}_{wb}^b\end{array}\right]\end{array}$$

同样在实际应用中，我们需要使用其离散形式，即：
$$\{\begin{array}{rl}{\mathbf{p}}_{\{k+1\}}^w& ={\mathbf{p}}_{\{k+1\}}^w+{\mathbf{v}}_{\{k\}}^w\Delta t+\frac{1}{2}{\mathbf{a}}_{\{k\}}^w\Delta t^2\\ {\mathbf{v}}_{\{k+1\}}^w& ={\mathbf{v}}_{\{k\}}^w+{\mathbf{a}}_{\{k\}}^w\Delta t\\ {\mathbf{q}}_{wb\{k+1\}}& ={\mathbf{q}}_{wb\{k\}}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{\omega }}_{wb}^b\Delta t\end{array}\right]\end{array}$$

其中四元数的离散更新用到了一阶毕卡近似算法。