数据结构与算法（笔记一）（Python）

学习笔记（一）

201：什么是算法

问题：动态类型语言的优缺点？python的一个显著特点就是动态类型，那么与c这种静态类型语言相比，它的优缺点都有哪些呢？
答：优点：灵活，可读性强；缺点：数据模型多，难以维护，不适合复杂的业务

问题：为什么Python的强制缩进是好的？
答：语句块功能和视觉效果统一

问题：为什么要研究算法？
答：简单求和例子

第一种迭代算法

import time


# 直接用for进行累加
def sum0fN2(n):
    start = time.time()
    theSum = 0
    for i in range(1, n + 1):
        theSum = theSum + i
    end = time.time()
    return theSum, end - start


# 运行有误差，所以运行5次
for i in range(5):
    print("Sum is {} required {:.7f} seconds".format(sum0fN3(10000)[0], sum0fN3(10000)[1]))

结果：

n = 10000结果为
Sum is 50005000 required 0.0009966 seconds
n = 100000结果为
Sum is 5000050000 required 0.0039897 seconds
n = 1000000结果为
Sum is 500000500000 required 0.0608370 seconds

可以看出n每次增加10倍，运行时间基本是线性增加。

但我们利用第二种方法，无迭代的累计算法呢？

# 采用求和公式的无迭代算法
def sum0fN3(n):
    start = time.time()
    theSum = (n * (n + 1) / 2)
    end = time.time()
    return theSum, end - start

for i in range(5):
    print("Sum is {} required {:.7f} seconds".format(sum0fN3(10000)[0], sum0fN3(10000)[1]))

结果为：

n = 10000结果为
Sum is 50005000.0 required 0.0000000 seconds
n = 100000结果为
Sum is 50005000.0 required 0.0000000 seconds
n = 1000000结果为
Sum is 50005000.0 required 0.0000000 seconds

时间不会随着n增加而增加（前面的是倍数增长关系），这种算法的运行时间比前面的短多了。
但运行时间的实际检测跟计算机的语言和硬件有关，所以我们比较算法运行时间是不可靠的。

202：大O表示法

算法时间度量指标

一个算法所实施的操作数量或者步骤可以作为独立具体程序的度量指标。
赋值语句是一个合适的选择
一条赋值语句同时包含了（表达式）计算和（变量）存储连个基本资源。
问题的规模影响算法的执行时间
在计算n个整数求和中，n=1000比n=100规模更大。
数量级函数
基本操作数量函数T(n)的精确并不是特别重要，重要的是T(n)中起决定性因素的主导部分，数量级函数描述了T(n)中随着n增加而增加速度最快的主导部分，称为“大o”表示法，记作o(f(n)),其中f(n)表示T(n)中的主导部分。
确定运行时间数量级大O的方法
例子1：T(n) = 1 + n
当n增大时，常数1在最终结果中显得越来越无足轻重，所以去掉1保留n作为主打部分，运行时间数量级就是O(n)。

例子2：$T(n)=5n^2+27n+1005$
当$n$很小时，常数1005其决定性作用
当n越来越大，$n^2$项就越来越重要，其它两项对结果的影响则越来越小
同样，$n^2$项中的系数5，对于$n^2$的增长速度来说也影响不大
所以可以在数量级中去掉27n+1005，以及系数5的部分，确定为O($n^2$)

有时决定运行时间的不仅是问题规模
某些具体数据也会影响算法运行时间
分为最好、最差和平均情况，平均状况体现了算法的主流性能
对算法的分析要看主流，而不被某几种特定的运行状况所迷惑

其他算法复杂度表示法

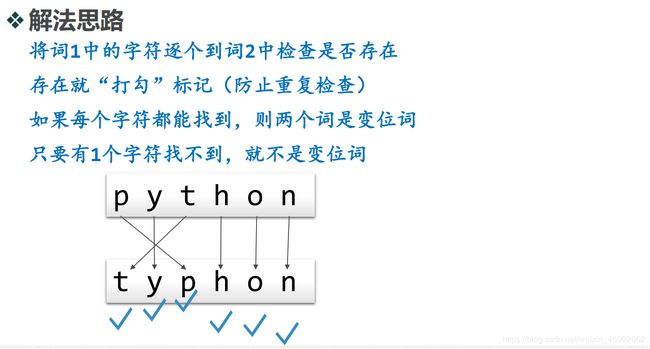
203：变位词

所谓“变位词”是指两个词之间存在组成字母的重新排列关系
如：heart和earth，python和typhon
为了简单起见，假设参与判断的两个词仅由小写字母构成，而且长度相等

解题目标：写一个bool函数，以两个词作为参数，返回这两个词是否变位词
可以很好展示同一问题的不同数量级算法

解法1：逐字检查


解法1：逐字检查-程序代码：

def anagramSolution1(s1, s2):
    # 复制s2到列表
    alist = list(s2)
    pos1 = 0
    stillOK = True
    # 循环s1的每个字符
    while pos1 < len(s1) and stillOK:
        pos2 = 0
        found = False
        while pos2 < len(alist) and not found:
            # 在s2逐个对比
            if s1[pos1] == alist[pos2]:
                found = True
            else:
                pos2 = pos2 + 1
        # 找到就打钩
        if found:
            alist[pos2] = None
        # 未找到就失败
        else:
            stillOK = False
        pos1 = pos1 + 1
    return stillOK


print(anagramSolution1('abcd', 'dcba'))

结果：

True

解法1：逐字检查-算法分析

解法2：排序比较

代码：

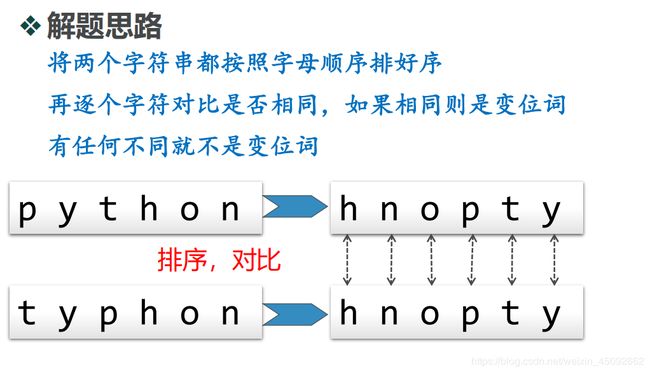
def anagramSolution2(s1, s2):
    # 转为列表
    alist1 = list(s1)
    alist2 = list(s2)

    # 分别排序
    alist1.sort()
    alist2.sort()
    pos = 0
    matches = True
    while pos < len(s1) and matches:
        if alist1[pos] == alist2[pos]:
            pos = pos + 1
        else:
            matches = False
    return matches


print(anagramSolution2('abcde', 'edcba'))

结果：

True

解法2：排序比较-算法分析

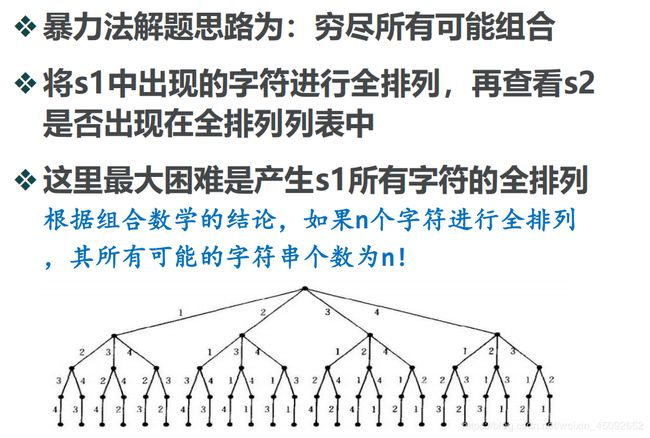
解法3：暴力法


解法4：计数比较

代码：

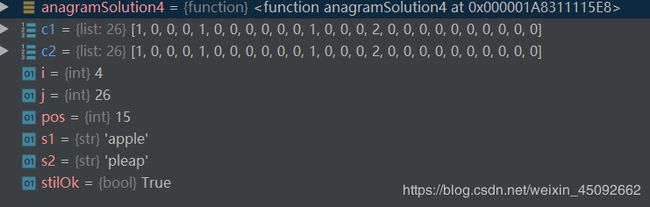
def anagramSolution4(s1, s2):
    c1 = [0] * 26
    c2 = [0] * 26
    # 分别计数
    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a')
        c1[pos] = c1[pos] + 1
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        c2[pos] = c2[pos] + 1
    j = 0
    stilOk = True
    while j < 26 and stilOk:
        if c1[j] == c2[j]:
            j = j + 1
        else:
            stilOk = False
    return stilOk


print(anagramSolution4('apple', 'pleap'))

设置断点调试的结果：

解法4：计数比较-算法分析


参考：北京大学，数据结构与算法（Python版）