OpenFOAM User Guide 第五章 翻译和阅读笔记

第五章网格生成和转化

 

    本章讲解与OpenFOAM中与网格生成的主题，5.1概要地讲解了网格在OpenFOAM中描述方法，5.3介绍了如何用blockMesh工具生成六面体简单网格，5.4部分介绍了如何用snappyHexMesh工具生成复杂的六面体网格和从三角型几何表面自动分割出六面体元，5.5部分介绍了再将第三方软件生成的网格转化成OpenFOAM可读格式过程中的可用选项。

 

5.1 网格的描述

 

    本部分提供了OpenFOAM C++类如何处理网格的详细说明。网格式数值计算过程中必须的一部分，必须满足一定的标准来确保有效和准确的计算。在任何一个计算运行的过程中，OpenFOAM都会检查网格是否满足一系列非常严格的有效性限制条件，在不满足条件的情况下就会终止运行。这样的结果就是用户在用OpenFOAM进行计算之前可能会消耗很多时间来“修改”由第三方程序生成的巨大的网格。这很令人沮丧，但是OpenFOAM并不会因此作出任何道歉，因为这只是为了确保网格可用所采取的必须措施，否则，计算可能在开始之前就已经有缺陷了。

    在默认情况下，OpenFOAM在三维下定义任意多面体元的网格，每个多面体元由任意多边形围绕成，即每个体元来讲，面的数量没有限制，而对每个面来讲，边的数量也没有限制，边的对齐方式也没有限制。在OpenFOAM中，具有这种通用结构的网格又被称为polyMesh，这种网格在生成和操作方面提供了很大的自由度，特别是在复杂几何形状区域或是随时间变化的网格。而使用这种网格的代价就是那些使用传统工具生成的网格很难转换。OpenFOAM库因此提供了cellShape工具通过一系列预定义的体元形状来管理传统网格的格式。

 

5.1.1网格说明和可靠性限制

 

    在描述OpenFOAM的网格格式，polyMesh和cellShape工具之前，先要说明一下OpenFOAM中使用的可靠性限制条件，网格必须满足的条件如下：

 

5.1.1.1点（point）

 

    点是三维环境下的一个位置，由单位是米的一个向量来定义。当点有很多时则被编译为一个list，并且每个点都使用一个表示在list位置的标签（label，编号顺序从0开始）来索引，list中既不能含有具有完全相同位置的两个不同点，也不能含有不属于任何平面上的点（点必须至少属于一个平面）。

 

5.1.1.2面（face）

 

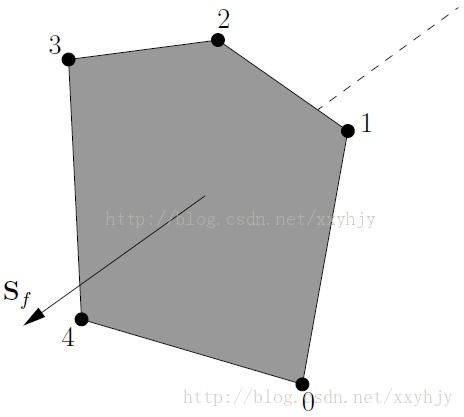
    一个面是是一个有序的点list（也就是说list中的元素是点），其中点都由它们的标签进行索引，list中两个相邻的点之间代表一个边（edge），即按照list索引顺序遍历一遍所有的点相当于在面的边缘上走了一圈。所有的面也被编译成一个list（也就是说这个list里面，每一个元素是面）并由表示在list位置的标签进行索引。面的法向量由右手定则来定义（用右手握住面的边缘，四个手指顺着点标签的升序（1-2-3-4~）顺序方向，大拇指的方向就是面的法向量方向）。

图 5.1 面的面积向量示意图

 

面的种类有两种：

内部面：这些面连接着两个体元（不可能超过两个），每个体元也有自己的标签，对于每个内部面来说，其法向量的方向指向那个标签号比较大的体元，例如连接2号和5号体元的内部面，其法向量指向标签号为5的体元。

边界面：这些面只属于一个体元，因为他们与计算区域的边界相连。因此这些面就由（而且是仅仅由）一个它们所属的体元以及一个boundary patch所标记。其点标签的顺序由其法向量的方向所定义，而边界面的法方向则被规定指向计算区域之外。

 

    面的形状通常都要求是一个凸多面性，至少要求面的中心位于面的内部。面允许弯曲，也就是说并不是所有的点都要求共面。

 

5.1.1.3体元（cell）

 

    一个体元是一个面list，面在list中的顺序是任意的。体元必须含有以下属性：

Contiguous（临近？接触性？）：所有的体元必须完整地覆盖计算区域，而且不能相互重叠。

Convex（凸多面体？）：每个体元必须是凸多面体，而且中心要在体元内部。

Closed（封闭性）：每个体元必须是闭合的，无论是几何上还是拓扑上。即：

    ·几何封闭性要求：当所有面的面积向量（面积向量——大小等于多边形的面积而方向与多边形相垂直）向外地指向体元外的一点时，它们的向量和应该等于零（机器精度内）。

    ·拓扑封闭性要求：体元所有的边都是由体元本身的两个面相交决定的，拓扑封闭性要求体元所有的边都必须完全地由体元的这两个面所拥有和使用，而不能延伸到第三个体元面上。

正交性：对于网格的内部面来说，我们定义一个中心对中心向量，中心对中心向量连接两个相互接壤的体元的中心，起点是标签编号较小的那个体元，终点是标签编号较大的那个体元。正交性限制要求对于每个内部面来说，面的面积向量与上述的中心对中心向量之间的夹角应该总小于90度。

 

5.1.1.4  边界（boundary）

 

    边界是一个patches的list，每个patch都与某个边界条件相关。patch是一系列边界面标签的list（并且patch仅含有边界面标签而不含有内部标签）。所有的边界要求必须是闭合的，也就是说所有边界面面积向量的向量和等于零（机器精度内）。

 

5.1.2 polyMesh的描述方式

 

    constant文件夹的子文件夹polyMesh中，含有一个完整的对于case的polyMesh的描述。polyMesh的描述是基于面的，正如前面所述的，内部面连接着两个体元，边界面则标记（address）了一个体元和一个boundary patch。因此，每个面都被赋予了一个拥有者体元（owner cell）和相邻体元（neighbour cell），这样，穿过一个给定面的连通性（connectivity）就可以用拥有者体元（owner cell）和相邻体元（neighbour cell）的标签编号来表达。对于边界上的面来说，与其相连的体元被作为拥有者体元，而相邻体元的体院标号被赋值为“-1”。因此，I/O过程标准输出中就包含了以下的文件：

 

点：一个向量list，用以描述体元的顶点，其中的list第一个点代表顶点0，第二个代表顶点1，以此类推。

面：一个面list，其实每个面也都是list（其中的元素就是前述的点list的标签编号），同样的，list中的第一项代表着面0，并以此类推。

拥有者：拥有者体元的标签编号list，其中元素的标签编号与面的标签编号直接相关，也就是说list中的第一个条目是面0的拥有者体元，并以此类推、

 

边界：一个patch的list，包含有每个patch的字典条目，声明用到的patch名称，例如：

movingWall
{
    type patch;
    nFaces 20;
    startFace 760;
}

其中，startFace是patch中第一个面在面list中的标签编号（the index into the face list of the first face in the patch）, nFaces是patch中的面数量。

注意如果用户想要了解在其计算区域内有多少个体元，可以参阅owner文件中头部FoamFile里的nCells条目。（Note that if the user wishes to know how many cellsare in their domain, there is a note in the FoamFile header of the owner file that contains an entry fornCells.）

 

5.1.3 cellShape工具

 

    在这里介绍可选工具cellShape，该工具可用来将一些标准的（较简单的）网格格式转换为OpenFOAM库可用的格式。

    现有的其他大多的数的网格生成工具和后处理系统仅支持一小部分可能多面体体元形状。它们以有限几种的三维体元形状为基础来定义网格，即体元形状。OpenFOAM库包含了这些标准形状的定义来实现这些网格向polyMesh的转化。

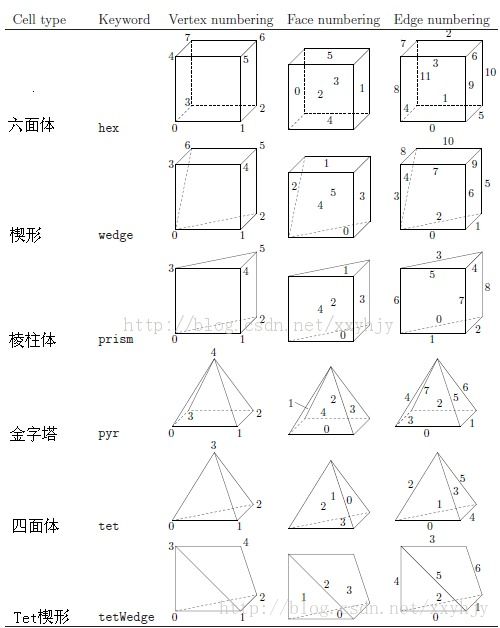
    OpenFOAM中所支持的cellShape模型列在表5.1中。表中模型说明了模型中点、边、面的编码方法，这些模型就是依靠着这样的编码顺序进行定义和描述的。如果点的顺序不按这个标准，就有可能出现体元形状的扭曲或退化成其他几何形状，换句话说在一个简单形状中同一个点的标签不能使用两次（the same point label cannot be used more that once in single shape，原文中的is疑应该为in，that疑应该为than）。此外，在OpenFOAM中不必要使用重复点（duplicate points），因为OpenFOAM中所有可用形状覆盖了所有的退化六面体形状。

    体元的描述包含了两部分，体元模型的名字和有序的标签编号list，因此，如果在体元描述过程中使用了如下的点list：

8
(
    (0 0 0)
    (1 0 0)
    (1 1 0)
    (0 1 0)
    (0 0 0.5)
    (1 0 0.5)
    (1 1 0.5)
    (0 1 0.5)
)

一个六面体体元就可以写成：

(hex 8(0 1 2 3 4 5 6 7))

其中hex是声明使用六面体网格的关键字。其他形状的的声明关键字见表5.1

表5.1 体元中顶点，面和边的标号顺序

5.1.4一维，二维和对称问题

 

    OpenFOAM在设计之初就是基于三维的，所有的网格都是在这种条件下定义的。但是，一维，二维和对称问题依然可以通过OpenFOAM，生成三维网格并使用特殊的边界条件来模拟。更具体地说，一维和二维问题使用empty型的patch类型，而轴对称问题可以用wedge类型。这两种类型的使用分别在5.2.2部分和5.3.3部分进行了论述。

 

5.2 边界

 

    在本部分中，我们将会讨论边界条件在OpenFOAM中的处理方法。边界的问题在建模的过程中也要涉及到，因为这一问题不仅与几何实体有关，也是数值计算过程中的重要部分，关系到边界条件和内部边界的相互连接的数值处理方法。关于边界处理的讨论也许并不适合放在网格，场，离散化和计算过程等问题的讨论之中，在这里说明边界条件的处理仅仅是为了方便。

    我们首先需要考虑，为了达到灵活应用边界条件的目的，一个边界首先被分解为一系列的patch。一个patch也许包含了一个或多个闭合边界面，但是并不一定在物理上是相连的。

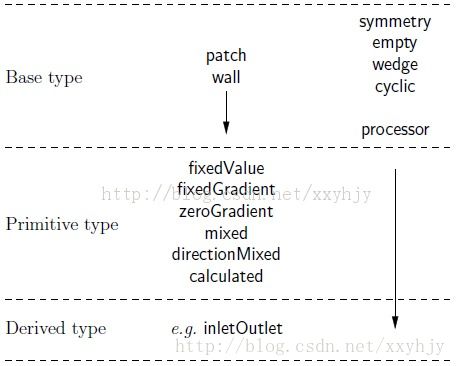
    每个patch有三个属性与之相关，表5.2按照patch不同的级别对这些patch的类型名字进行了介绍。下面的级别与OpenFOAM库中的类级别描述很相似，但并不完全相同。

 

Base型：  这种类型的边界条件仅仅是针对几何而言的，或者是描述了边界数据是怎么连接的（data ‘communication link’）。 

Primitive型：在Base型的基础上附带了某个场变量。

Derived型：复杂的边界条件，从Primitive型派生出来，附带有场变量。

表5.2 patch属性

 

5.2.1 OpenFOAM中的patch类型说明

 

    patch类型在OpenFOAM的case文件的场文件和网格中说明了，现做更进一步的说明：

    ·boundary文件中对每个patch都有type关键字来说明patch的Base类型，这个文件在constant/polyMesh文件夹中。

   ·数值patch类型，可以为Primitive或者Derived类型，在场文件中每个patch的type关键字后面指定。

    以下是sonicFoam的boundary实例，后面是同一个case的压力场。

17
18     6
19     (
20         inlet
21        {
22             type patch;
23             nFaces 50;
24             startFace 10325;
25         }
26         outlet
27         {
28             type patch;
29             nFaces 40;
30             startFace 10375;
31         }
32         bottom
33         {
34             type symmetryPlane;
35             nFaces 25;
36             startFace 10415;
37         }
38         top
39         {
40             type symmetryPlane;
41             nFaces 125;
42             startFace 10440;
43         }
44         obstacle
45         {
46             type patch;
47             nFaces 110;
48             startFace 10565;
49         }
50         defaultFaces
51         {
52             type empty;
53             nFaces 10500;
54             startFace 10675;
55         }
56         )
57
58 // *************************************************************************//
17 dimensions [1 -1 -2 0 0 0 0];
18
19 internalField uniform 1;
20
21 boundaryField
22 {
23     inlet
24 {
25     type fixedValue;
26     value uniform 1;
27 }
28
29 outlet
30 {
31     type waveTransmissive;
32     field p;
33     phi phi;
34     rho rho;
35     psi psi;
36     gamma 1.4;
37     fieldInf 1;
38     lInf 3;
39     value uniform 1;
40 }
41
42 bottom
43 {
44     type symmetryPlane;
45 }
46
47 top

48 {
49     type symmetryPlane;
50 }

51
52 obstacle
53 {
54     type zeroGradient;
55 }
56
57 defaultFaces
58 {
59     type empty;
60 }
61 }
62
63 // *************************************************************************//

    对于所有的patch来说，边界条件文件中的类型都是patch，除了那些具有几何形状限制的，例如symmetryPlane和empty类型的patch。压力文件中包含了primitive类型，并应用在了inlet和bottom面，一个更复杂derived类型应用在outlet。通过比较两个文件可以发现，当base类型不是简单patch时，base类型和数值类型（numerical type）是一致的，例如symmetryPlane和empty的patch。

 

5.2.2 Base类型

 

    Base和几何类型的描述如下，OpenFOAM中指定这些类型的关键字在图5.2中进行了总结。

图 5.3 轴对称几何情况下使用的wedge类型的patch

表5.2 Basic patch类型

关键字	描述
patch	一般的patch
symmetryPlane	对称面
empty	二维条件下的前后面的边界条件
wedge	轴对称几何条件下的楔形前后面边界条件
cyclic	柱状面
wall	湍流中所使用的壁面函数
processor	内部processor边界

 

patch：基本的patch类型，用于描述那些网格上没有几何和拓扑信息的patch条件（除了wall壁面条件以外），例如出入口（inlet和outlet）。

wall：有一些实例中，一个patch要求与一个壁面的情况尽可能一致，特别是那些特别进行建模的壁面边界条件。一个很好的例子是湍流壁面的建模，在这种情况下壁面边界条件必须指定一种壁面patch类型，这样，壁面到临近壁面体元中心的距离也作为patch信息的一部分存储起来。

symmetryPlane：用于对称面

empty：由于OpenFOAM总是产生三维几何体，但是也可以用来解决一维或者二维的问题，这就需要在那些与不需要求解的维度垂直的patch平面上指定特殊的empty条件。

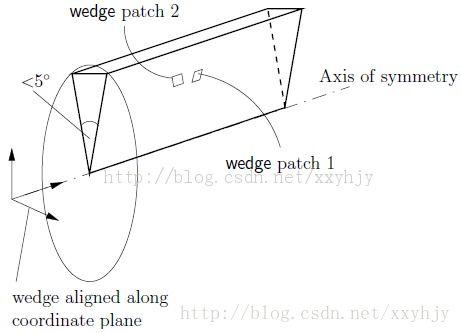
wedge：对于二维的轴对称case，例如圆柱体，几何体则被指定为一个夹角很小的楔体（<5°），沿着对称面为一个体元的厚度，并沿着一个坐标平面叉开，就像图5.3所示。轴对称的楔体的两个平面必须被指定为两个分开的wedge型patch。使用blockMesh产生楔体形状的几何的详细方法会在5.3.3部分说明。

cyclic：让两个patch像被物理连接起来一样进行处理，用于重复的几何形状，例如换热器管束。一个cyclic型patch通过boundary文件中的neighbourPatch关键字来与另一个cyclic的patch进行连接。每一对相互连接的的面的面积差都必须符合一定的允许误差，该误差值由boundary文件内的matchTolerance关键字定义。面并不需要具有相同的指向。

Processor：如果代码是在几个处理器上并行计算，那么网格就必须分为几个部分，使得每个处理器计算的体元数量大概相当。这样分成的不同区域之间的边界就称为Processor边界。

 

5.2.3 Primitive类型

 

    所有的primitive类型都列在表5.3中。

 

 

 

5.2.4 Derived类型

 

    在OpenFOAM中很多的derived类型的边界条件而无法一一列举，在表5.4中有选择性的列举了一些。如果用户想获得全部可用的模型，那么应该自习研究一下OpenFOAM的源代码。derived类型的边界条件相关源代码可在以下文件中找到：

 

·在$FOAM_SRC/finiteVolume/fields/fvPatchFields/derived

 

·对于一些特定的模型库，则可以在终端中使用如下的命令来定位代码：

 

find $FOAM_SRC -name"*derivedFvPatch"

 

·对于一些特定的解算器，则可以在终端中使用如下的命令来定位代码：

 

find $FOAM_SOVLER -name "*derivedFvPatch"

 

表5.3 Derived patch类型

类型	φ物理场patch的描述	需要给定的数据
fixedValue	指定物理量φ的值	φ的值
fixeGradient	指定物理量φ的法向梯度	φ的法向梯度
zeroGradient	指定物理量φ的梯度为0	—
calculated	边界上物理量φ的场是从其他物理量场计算而得	—
mixed	根据参数valueFraction来决定是使用fixedValue还是fixedGradient	refValue refGradient valueFraction value
directionMixed	带有valueFraction张量的混合条件。例如：在法向和切向具有不同混合程度的情况。	refValue refGradient valueFraction value

 

表5.4 Derived patch场类型

从fixedValue中派生的类型		需要指定的数据
movingWallVelocity	替换patch法向方向的值，这样通过patch的流量就为0	替换的值
pressureInletVelocity	入口处的压力p是已知的，U从流量中估算出来，与patch垂直	压力p值
pressureDirectedInletVelocity	入口处的压力p是已知的，U从流量inletDirection方向上计算出来	压力p值，inletDirection方向
surfaceNormalFixedValue	指定向量边界条件，其方向与patch方向垂直，对于指向区域外部的向量+ve。 （原文Specifies a vector boundary condition, normal to the patch, by its magnitude; +ve for vector pointing out of the domain.）	值
totalPressure	固定总压的值，当U变化时，p会自动调整	P0
turbulentInlet	在平均值的基础上计算一个脉动的变量	referenceField fluctuationScale
从fixedGradient/zeroGradient派生出的类型
fluxCorrectedVelocity	计算U在进口处的法向分量	分量值
wallBouyantPressure	根据气氛压力梯度设置压力梯度为固定值	—
从mixed派生出的类型
inletOutlet	根据U的方向在fixedValue和zeroGradient之间变化U和p的值	inletValue，value
outletInlet	根据U的方向在fixedValue和zeroGradient之间变化U和p的值	outletValue，value
pressureInletOutletVelocity	将pressureInletVelocity和inletOutlet组合在一起	值
pressureDirectedInletOutletVelocity	将pressureDirectedInletVelocity和inletOutlet组合在一起	值 inletDirection
pressureTransmissive	将超音速压力波传递给周围的压力场p∞	pInf
supersonicFreeStream	将斜激波传递给周围的p∞，T∞，U∞	pInf，TInf，UInf
其他类型
slip	如果物理量φ是标量，则用zeroGradient；如果φ是向量，那么法向分量设置为固定值fixedValue 0，切向分量为zeroGradient。	—
partialSlip	将zeroGradient和slip两个条件混合在一起，具体选哪个取决于valueFraction，如果valueFraction=0，则用slip	valueFraction

 

5.3 使用blockMesh工具生成网格

    本部分主要讲解OpenFOAM提供的网格生成工具blockMesh。blockMesh工具可以使用加密和曲线边来创建的带参数的网格。

    blockMesh从case文件夹中的constant/polyMesh文件夹中读取blockMesh字典文件并生成网格。blockMesh读取该文件后，生成网格，并将网格数据写入位于同一文件夹中points，faces，cells，boundary等文件中。

    blockMesh背后的原理是将集合区域分解为一个或者更多个三维区域，即六面体区块。区块的边可以是直线，弧或者样条。从表面上看，网格就是就是在区块各个方向上指定一系列体元，需要为blockMesh提供足够的信息来产生网格数据。

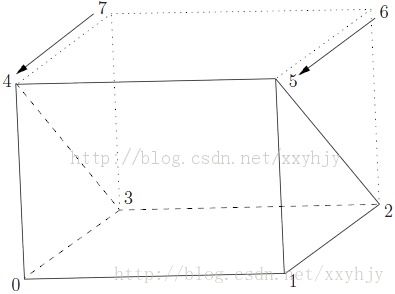
    每个几何区块由8个顶点来定义，每个顶点都位于六面体的角。每个顶点都被写入到一个list中，这样每个顶点都可以通过其标签编号来访问（记住OpenFOAM总是采用C++的传统，即标签编号的其实是从0开始）。图5.4所示的是一个区块的实例，每个顶点都按照其在list中的顺序进行了编号，其中连接顶点1和5的边是一条曲线，这主要是提醒用户在blockMesh中是可以指定曲线作为边的。

    使用少于8个点来产生区块也是可能的，例如将一对或者更多的点依次摞在一起，详见5.3.3所述。

    每个区块都拥有自己的右手坐标系(x1,x2,x3)。坐标系位置的定义与区块中点顺序的定义相关，遵循以下的规则：

·  坐标的原点位于区块定义中，编号为0的顶点。

·  x1的方向由从顶点0到顶点1的移动方向来定义。

·   x2的方向由从顶点1到顶点2的移动方向来定义。

·   由顶点0、1、2、4来定义平面x3=0.

·   顶点4位于从顶点0沿x3方向移动的路径上。

·   类似的，顶点5、6和7都位于从顶点1、2和3起始的沿x3方向移动的路径上。

 表5.5 blockMeshDict中的关键字

关键字	描述	实例
convertToMeters	顶点坐标的比例缩放因子	设置为0.001时，数值就缩放到了单位为mm
vertices	顶点坐标的list	(0, 0, 0)
edges	用来描述弧形（arc）或者样条（spline）的边	arc 1 4 (0.939 0.342 -0.5)
block	有序的顶点标签编号list，以及网格的尺寸	hex(0 1 2 3 4 5 6 7) (10 10 1) simpleGrading(1.0 1.0 1.0)
patches	patch的list	symmetryPlane base((0 1 2 3))
mergePatchPairs	需要合并的patch的list	参见5.3.2节

 

5.3.1编写一个blockMeshDict文件

 

    blockMeshDict文件是一个使用表5.5所示的关键字的字典文件。其中convertToMeters关键字指定一个比例因子，所有在网格中描述的顶点坐标都会与该因数相乘，例如：

 

        convertToMeters 0.001

   

    这意味着所有的顶点坐标都会乘以0.001参与运算，也就是说这个值说明blockMeshDict中引用的所有数值单位都是mm。

 

5.3.1.1顶点

 

    下面给出了一个网格中块的顶点的标准list，名字为vertices，以图5.4中的块为例：

    vertices

    (

        (0   0    0)       //0号顶点

        (1    0   0.1)    //1号顶点

        (1.1 1   0.1)       //2号顶点

        (0   1    0.1)       //3号顶点

        (-0.1-0.1  1)       //4号顶点

       (1.3  0   1.2)       //5号顶点

        (1.4  1.11.3)       //6号顶点

        (0 11.1)             //7号顶点

    )

 

5.3.1.2边

 

    默认情况下连接两个定点的边是直的，但是任何边都可以通过在名字为edges的list中的条目来指定为曲线。该list是可选的，即如果几何空间中不包括曲线，就可以忽略这个list。

    针对曲线边每个条目使用以下表格中的关键字来指定曲线的类型。

表 5.6 blockMeshDict字典文件中可用的边类型

 

可选关键字	描述	需要补充的参数
arc	使用圆弧连接	圆弧通过的一个点
simpleSpline	使用样条曲线连接	一系列内部点
polyLine	使用一系列直线连接	一系列内部点
polySpline	使用一系列样条曲线连接	一系列内部点
line	直线连接	-

 

    关键字后面就是边所连接的两个顶点的标签编号，在紧随其后的是必须指定的这条边所通过的点。当使用arc关键字指定一段弧线时，需要指定该弧线所在圆通过的一个点；对于使用simpleSpline，polyLine和polySpline关键字时，则需要一个内部点的list；使用line关键字即为采用默认情况下的直线，不需要内部点。注意本来并不需要line关键字，但是为了完整性还是加入了关键字列表。对于我们图5.4中的例子来说，我们指定连接顶点1和5之间的边为弧线arc，且该弧线通过内部点(1.1, 0.0, 0.5)。

    edge

    {

        arc  1  5  (1.1  0.0 0.5)

    }

 

5.3.1.3块 （blocks）

        块的定义包含在名称为blocks的list中，每个定义都是一个复合条目，其中包含顶点标签编号的list（在list中的顺序参见5.3），一个描述了在三个方向所需要的体元数量的向量，三个方向体元扩展比例的类型和数值。

        blocks以如下的方式进行定义:

    blocks

    (

        hex (0  1  2  3  4  5 6  7)    //顶点的标签

        (10  10  10)

        simple (1  2  3)

    )

    每个块的定义如下:

    顶点编号: 第一个条目是块的形状标志，在OpenFOAM-2.1.1/cellModels文件中定义，形状标志都是hex因为块一般都是六面体，其后紧跟着一个顶点编号的list，编号顺序由137页所述的方式进行编排.

    体元数量: 第二个条目给出的块是在三个方向x1，x2和x3上的cell数量。

    体元扩展比例: 第三个条目给出了块三个方向的体元扩展比例。扩展比例使得网格可以在特定方向上被划分或者加细，在某个方向上的扩展比例指的是块上该方向最后一个体元的宽度与起始宽度之比，如图5.5所示。以下的每个关键词则指定了使用哪一种blockMesh支持的划分方式，blockMesh支持两种划分方式。
        simpleGrading: 指定在三个方向上使用均匀扩展比例，并分别指定这三个比例大小。

            simpleGrading (1  2 3)

        edgeGrading: 针对每个边界分别给出完整的cell比例，编号方式则按照图5 .4，图中的箭头所示的方向就是从第一个体元到最后一个体元的方向。

            simpleGrading (1  1 1  1  2  2  2  2  3  3  3 3)

    这个设置的意思是说沿着边0~3的比例是1，沿着4~7的比例是2，沿着边8~11的比例是3，其效果与上面使用simpleGrading的效果是一样。

图 5.5  

5.3.1.4边界

        网格的边界在名字为boundary的list下面定义。boundary被打断成数个patch（也就是区域），其中list中的patch名字是由使用着自己决定的（尽管如此，我们还是建议使用比较较为方便且含有一定意义的名字，如 inlet），并会成为关键字，并在后续的步骤中使用，以指定场数据中使用的边界条件。接下来，patch的信息就会被保存在子文件夹下，这些信息包括：

        类型：patch的类型，可以是普通的边界条件，也可以是特殊几何条件。可参见表5.2以及5.2.2章节的描述。

        面：围成patch的面，是一个list并且这个list的名称用户也可以自己指定（尽管如此，我们还是建议使用比较较为方便且含有一定意义的名字，如 inlet），这个名字会在后续的步骤中使用，以指定场数据中使用的边界条件。

        blockMesh会自动将boundarylist中忽略的面补齐，并把它们赋予默认的边界条件defaultFaces，也就是empty类型。这说明对于二维几何条件下，使用者可以忽略掉位于二维平面上面的边界条件，blockMesh会自动赋予默认的empty类型值。

        回到图5.4中的示例块，如果他的左面是入口，右面是出口，其他四个面是墙壁，那么就可以使用如下的定义：

 

    boundary

    (

        inlet

        {

            type  patch;

            faces

            (

                (0 4 7 3)

            );

        }

 

        outlet

        {

            type  patch;

            faces

            (

                (1 2 6 5)

            );

        }

       

        walls

        {

            type wall;

            faces

           (

                (0 1 5 4)

                (0 3 2 1)

                (3 7 6 2)

                (4 5 6 7)

           );

        }

    )

 

        每个面都由4个顶点组成的list来定义，点描述的顺序必须遵循以下规则：当从块内部向外看时，描述的点的顺序是顺时针围绕面的一圈。

        当在blockMesh中指定了cycle类型的patch，那用户就必须使用neighbourPatch关键字同时指定相关cycle类型patch的名字。例如：

    left

    {

        type  cycle;

        neighbourPatch right;

        faces  ((0 4 7 3));

    }

 

    right

    {

        type  cycle;

        neighbourPatch left;

        faces  ((1 5 6 2));

    }

 

5.3.2多重块

        网格可以采用多个块来创建。在这种情况下，网格生成过程也是同样的步骤，唯一需要补充的块与块之间的连接方式，主要有两种：

面匹配: 两个块的patch中共用一组面，这些面同时属于两个块并拥有同样的顶点。

面合并:  两个块的patch中相互连接的一组面，这些面形成一组新的内部面来连接两个块。

        当使用面匹配来连接两个块的时候，需要在patch list中忽略块上相应的patch，这样，blockMesh会识别出没有形成外部边界的面，并将并置排列的面对组合成一个单一的内部面，换句话说，这些内部面会连接来自不同块的体元。

        另一个选择是面合并，该方式要求要合并的块的patch首先要在patch list中定义，两个patch中每一对要合并的面都必须在名字为mergePatchPairs中声明，mergePatchPaires的格式如下：

mergePatchPairs

{

    ( )  //mergepatch 0

    ( )  //mergepatch 1

}

    上面的声明中，第一个patch被当做为主patch，后面的则作为是从patch。合并的规则如下：

· 主patch的面保持原始的定义，其所有的顶点都位于原始位置。

· 在主/从patch之间有间隙的地方，将从patch的面投影到主patch的面上。

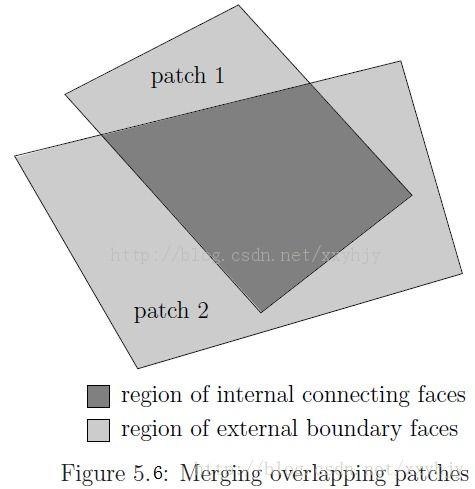
· 当两个patch发生如图5.6所示的重叠的时候，执行上述两条规则后仍然不能合并的部分，变成原始patch的外部面，其上必须赋予相应的边界条件。

· 如果一个patch的所有面都被合并的话，这个patch将不会再含有面，并被移除。

        使用该方式的直接结果就是，从patch的原始几何形状往往不会在合并过程中保存下来。因此，在一个算例中，当一个圆柱形的块和一个较大的块相连时，较为明智的作法是将圆柱形的块上的patch作为主patch，这样圆柱形的几何形状就可以正确的保留下来。除此之外，还有如下的补充建议来确保成功的合并过程。

·  在二维几何条件下，第三维中体元的尺寸，即在二维平面的外部，应该与二维平面上体元的高和宽差不多。

· 不建议重复合并一个patch两次，即，让一个patch出现在mergePatchPairs中两次。

· 当两个需要合并的patch共用一个边时，两个patch都需要被声明为主patch。

 

5.3.3在少于8个顶点的情况下创建块

 

        在一定情况下可以将成对（或多个成对的）的两个顶点相互合并缩减成一个顶点，以从数量少于8个的顶点上创建一个块。最常见的例子就是针对5.2.2节中某些二维轴对称算例中需要运用到wedge类型的patch的情况，这时会需要创建6面楔形块。图5.7直观地表现了这一过程：即顶点4和7合并成单一顶点4，而顶点5和6合并成单一顶点5。在声明块时只要像如下所示分别将顶点7和6替换为4和5即可：

    hex(0  1  2  3  4  5 5  4 )

 

图 5.6 使用6个顶点创建一个楔形的块

 

        同样的情况也发生在声明patch时，patch中包含的一个边界面因为点的合并而退化，合并前为(4 5  6  7) ，但是合并后则变为(4  5  5  4)（原文：The same applies tothe patches with the main consideration that the block face containingthe collapsed vertices, previously (4  5  6  7) now become(4  5  5  4). ）。对于这个块来说，点合并的结果是创造了面积为0的面，在polyMesh文件夹的boundary文件中，则是创建了一个不包含任何面的patch。在blockMeshDict中，这个patch应该被指定为empty类型，而边界条件也因此需要被指定为empty。

（未完待续）