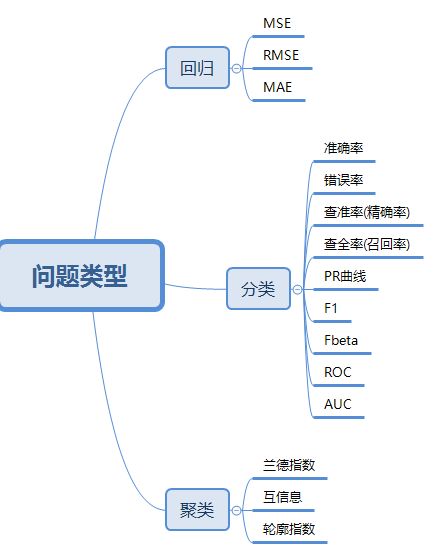
回归和分类模型性能评估指标MSE,MAE,PR,ROC,AUC
文章目录
- 0. 模型评估是什么,为什么
- 1. 不同类型问题的评估指标
- 1.1 回归问题
- 1.2 分类问题
- 1.2.1 准确率和错误率
- 1.2.2 精确率和召回率
- 1.2.3 PR曲线图
- 1.2.4 F1值
- 1.2.5 ROC
- 1.2.5.1 ROC引入
- 1.2.5.2 ROC解读
- 1.2.6 AUC值
- 1.2.7 ROC 和 PR
- 3. 参考文献
0. 模型评估是什么,为什么
模型评估其本质是为了解决模型的泛化问题,由于各种原因,训练完成的模型可能会产生过拟合和欠拟合问题,因此需要对模型评估其泛化能力,并进行合适的参数调整以求得模型最优。
为什么要进行模型评估?
除了考虑到模型泛化能力的问题,同时也要兼顾不同业务场景下的业务指标不同。对于不同的业务场景,选择对应的评估指标,可以更加明确优化目标,从而使得模型达到一种实用业务场景的优化。
总而言之,模型评估是为了模型调参服务,使得模型能够更好的用于实际的业务场景下。
1. 不同类型问题的评估指标
1.1 回归问题
回归问题,在小蓝书P4的定义:输入和输出都是连续变量的预测问题。
评估连续变量预测性能,有三种指标:
- MSE 均方误差
M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 MSE = \frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2} MSE=m1i=1∑m(yi−y^i)2
这个指标就是线性回归的最小二乘法损失函数,将其作为模型的预测性能评估指标,也是简单直观的。 - RMSE 均方根误差
R M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 RMSE = \sqrt{\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}} RMSE=m1i=1∑m(yi−y^i)2
这个从评估角度,本质上与MSE相同。但是从解释性来看,RMSE的量纲是友好的,比如房价预测,通过开方我们可以直接描述模型误差为多少万元,而不是多少万元的平方。 - MAE 平均绝对误差
M A E = 1 m ∑ i = 1 m ∣ ( y i − y i ) ∣ MAE = \frac{1}{m} \sum_{i=1}^{m}\left|\left(y_{i}-y_{i}\right)\right| MAE=m1i=1∑m∣(yi−yi)∣
这个解释性来看和RMSE相同,都是量纲友好的。
对于RMSE和MAE来看,由于RMSE涉及到误差的平方,可能对于异常值比较敏感,得到的误差比较大。如果同等维度来看,RMSE和MAE看哪个都可以。如果要从数据来得到比较乐观的结果,MAE看起来更小更好,如果看进步RMSE会更好。所以具体选用哪个评价指标,那得看你想怎么解释自己的模型。
1.2 分类问题
具体来看分类模型的评估可以分为三大类来看待,不同类别有自己衍生的一套体系。
在看评估指标之前,我们先看一下混淆矩阵如下图所示:

其中, 行坐标为预测(predicted)类别,列坐标为真实(actual)类别。
T N TN TN:真负类,表示真实为负并且预测为负的样本。
F N FN FN:假负类,表示真实为正但是预测为负的样本。
F P FP FP:假正类,表示真实为负但是预测为正的样本。
T P TP TP:真正类,表示真实为正并且预测为正的样本。
1.2.1 准确率和错误率
- 错误率(error rate)
E = ( F P + F N ) / M E=(FP+FN)/M E=(FP+FN)/M,表征错误分类样本占比 - 准确率(accuracy)
A = ( T P + T N ) / M A=(TP+TN)/M A=(TP+TN)/M,表征正确分类样本占比
其中, M = T P + T N + F P + F N M=TP+TN+FP+FN M=TP+TN+FP+FN
错误率和准确率是强相关的,大多情况下可单独关注准确率一个指标。它是我们最简单直观的度量方式,比如人脸识别100张图片,识别出99张,可以说准确率为99%。
但是,它有先天的劣势,对正负样本不平衡的问题,无法给出客观的评价。比如正确样本占比90%,我的预测模型可以直接预测所有样本为正,准确率即为90%,但显然是错误的。
1.2.2 精确率和召回率
当我们关心“选出来的好瓜中,有多少比例是真的好瓜”以及“所有好瓜,有多少被选出来了”,这些都无法使用“准确率”来衡量。
对应以上两个问题,有以下两个评估指标。
- 精确率(precision,查准率)
P = T P T P + F P P=\frac{T P}{T P+F P} P=TP+FPTP,表征被被判断为正类的所有样本中,真正类的占比。
分母是被判断为正类的样本总和。
比如,判断食品是否安全,我们更关心查准率。即挑出合格的食品中,有多少是真合格的。 - 召回率(recall,查全率)
R = T P T P + F N R=\frac{T P}{T P+F N} R=TP+FNTP,表征所有正类样本中,被识别为真正类的占比。
分母是真实为正类的样本总数。
比如,判断一个人是不是小偷,我们更关心查全率。即所有小偷中,有多少被找出来了。
两者的区别,关键在于分母,一个是判断为正,一个是真实为正。
1.2.3 PR曲线图
精确率和召回率本身是一对相互矛盾的指标,想要精确率高,就要提高阈值把更有把握的判断为正,但是想要召回率高,就要降低阈值,将更多的正类囊括进来,因此,可以将两者关系绘制为PR曲线图。
按照判断正类样本的可能性对所有样本排序,一次把一个样本归为正类,计算P和R,绘制曲线如下:
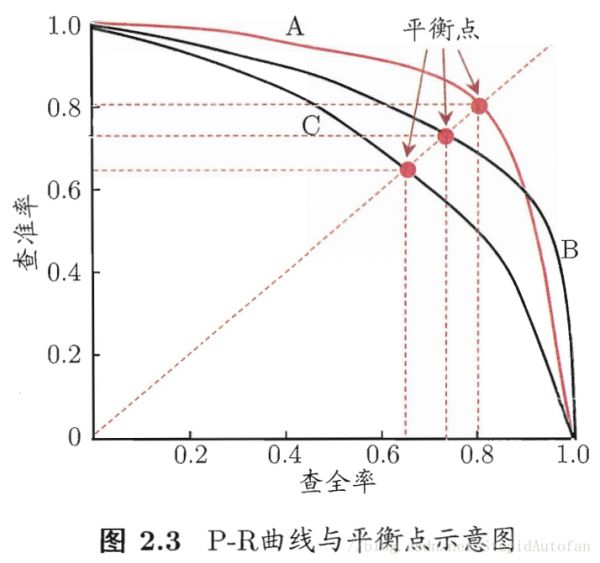
- B学习器的PR曲线完全包裹C学习器, 可以断言B性能优于C。
- A和B有交叉,不能断定两者优劣。可以通过A和B的包裹面积,可以做大概评估。
- 通过平衡点(break-even point/ BEP) P = R时,A的平衡点高于B,可以认为A优于B。
通过BEP思想进一步演化除了F1分值。
1.2.4 F1值
定义, 2 F 1 = 1 P + 1 R \frac{2}{F_{1}}=\frac{1}{\text { P}}+\frac{1}{\text { R}} F12= P1+ R1
推导得, F 1 = 2 T P 2 T P + F P + F N F_{1}=\frac{2 T P}{2 T P+F P+F N} F1=2TP+FP+FN2TP
F1可以看成是综合考虑P和R的性能的指标,但是具体P和R哪个大,哪个小没有界定。
这时候衍生出了 F β F\beta Fβ
1 F β = 1 1 + β 2 ⋅ ( 1 P + β 2 R ) \frac{1}{F_{\beta}}=\frac{1}{1+\beta^{2}} \cdot\left(\frac{1}{P}+\frac{\beta^{2}}{R}\right) Fβ1=1+β21⋅(P1+Rβ2)
F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R F_{\beta}=\frac{\left(1+\beta^{2}\right) \times P \times R}{\left(\beta^{2} \times P\right)+R} Fβ=(β2×P)+R(1+β2)×P×R
其中, β > 0 \beta>0 β>0,它度量了P和R的相对重要性,当 β = 1 \beta = 1 β=1,退化为F1值。当 β > 1 \beta >1 β>1,R更重要,当 β < 1 \beta<1 β<1,P更重要。
1.2.5 ROC
1.2.5.1 ROC引入
ROC 全名是受试者工作特征(Receiver Operating Characteristic)曲线。涉及到以下两个指标:
-
TPR = T P T P + F N \operatorname{TPR}=\frac{T P}{T P+F N} TPR=TP+FNTP,灵敏度也叫真正类率,其实和召回率定义一样。
-
FPR = F P T N + F P = 1 − 特 异 度 \operatorname{FPR}=\frac{F P}{T N+F P} = 1- 特异度 FPR=TN+FPFP=1−特异度,假正类率
特异度 = T N / ( F P + T N ) =\mathrm{TN} /(\mathrm{FP}+\mathrm{TN}) =TN/(FP+TN)
两者对应到混淆矩阵,注意这个图与本节开头的图少许区别,预测和实际调换了位置,如下图所示:

绘制ROC曲线,按照判断正类样本的可能性对所有样本排序,一次把一个样本归为正类,计算TPR和FPR,如下图。
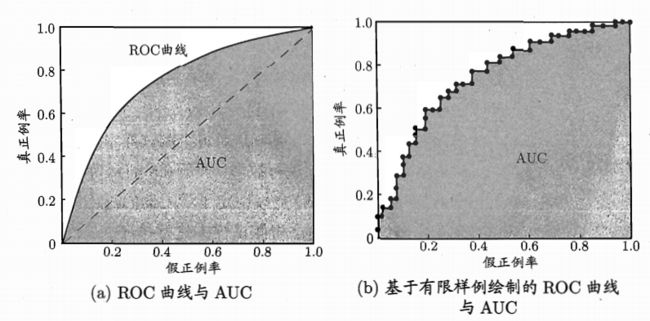
可以看出,TPR和FPR分别是基于实际样本的正负来考察的,也就是说它们分别在实际的正样本和负样本中来观察相关概率问题。
1.2.5.2 ROC解读
比如,90%是正样本,10%是负样本,用准确率是有水分的,但是用TPR和FPR不一样。
TPR只关注90%正样本中有多少是被真正覆盖的,而与那10%毫无关系,同理,FPR只关注10%负样本中有多少是被错误覆盖的,也与那90%毫无关系,所以可以看出:如果我们从实际表现的各个结果角度出发,就可以避免样本不平衡的问题了,这也是为什么选用TPR和FPR作为ROC/AUC的指标的原因。
-
如何评价ROC好坏?
FPR表示模型虚报的响应程度,而TPR表示模型预测响应的覆盖程度。TPR越高,同时FPR越低(即ROC曲线越陡),那么模型的性能就越好。
所以如果A的ROC包裹B的ROC,则A学习器更好。
如果A,B有交叉,则不能断言,这时候引入了AUC值。 -
ROC曲线无视样本不均衡
当样本不均衡时,准确率是不准确的。PR曲线会明显改变形状,而ROC则不受影响。因为ROC相当于固定一个轴,即实际正类或者实际负类的评价。
1.2.6 AUC值
AUC(Area under curve)是为了通过ROC曲线,评价A和B学习器好坏而提出的。
ROC曲线图对角线,它的面积正好是0.5。对角线的实际含义是:随机判断响应与不响应,正负样本覆盖率应该都是50%,表示随机效果。ROC曲线越陡越好,所以理想值就是1,一个正方形,而最差的随机判断都有0.5,所以一般AUC的值是介于0.5到1之间的。
最理想的情况下,没有真实类别为1而错分为0的样本,TPR一直为1,于是AUC为1,这便是AUC的极大值。
AUC的一般判断标准:
0.5 - 0.7:效果较低,但用于预测股票已经很不错了
0.7 - 0.85:效果一般
0.85 - 0.95:效果很好
0.95 - 1:效果非常好,但一般不太可能
1.2.7 ROC 和 PR
ROC兼顾了正类和负类的分类能力,同时对类别不均衡问题处理很好。
PR仅仅关注正类,如果在更关注正类的评价学习器时,选择PR曲线。除此,大部分时候用ROC即可。
聚类问题,暂时不做记录。
3. 参考文献
https://zhuanlan.zhihu.com/p/34655990
https://www.zhihu.com/question/30643044/answer/510317055
https://www.zhihu.com/search?type=content&q=ROC%E5%92%8CAUC