旋量初识

一、前言

在之前的博文坐标旋转中，简单介绍了平面坐标系以及三维坐标系中的绕坐标轴旋转运动。在机器人运动中，除了坐标系的旋转外，往往还要考虑平移运动，在三维空间中，刚体的旋转运动可以用绕一根轴的螺旋运动来描述。接下来，我们将逐步引出旋量的概念。

二、预备知识

刚体在坐标系中的运动，一般情况下是平移运动与旋转运动的结合，特殊情况是纯平移运动或纯旋转运动。

2.1 平移运动

在上图中，坐标系 $A$ 平移到坐标系 $B$，可以用 $\pmb p_{ab}$ 表示平移关系。假设，$B$ 坐标系中的任一点 $Q$，在 $B$ 系中的坐标可用向量 $\pmb p_b$ 表示，$Q$ 在 $A$ 系中的坐标可以用 $\pmb p_a$ 表示，显然有： $$ \pmb p_a = \pmb p_{ab} + \pmb p_b \tag{2-1} $$

2.2 旋转运动

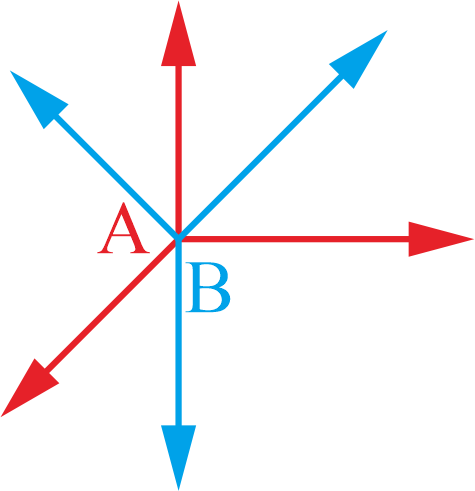
坐标旋转运动的基本思想在博客坐标旋转中已经有了介绍，这篇文章中只是介绍了绕单轴旋转的情况，对于不是绕单轴的旋转运动，可以由多次绕不同的单轴旋转运动来得到，例如上图中从$A$系(即参考坐标系)到$B$系(即本体坐标系)，可以通过先绕$A$的$Z$轴旋转得到$C$系(图中未画出)，再绕$C$系的$Y$轴来旋转得到$B$系(这里只是举例说明，也可以有其他的旋转方式)。那么，$B$系中的点在$A$中的表示方式可为：
$$\begin{gathered} {p\text{p}p}_A{=}^A{T\text{T}T}_C\cdot {p\text{p}p}_C \\ {p\text{p}p}_C{=}^C{T\text{T}T}_B\cdot {p\text{p}p}_B \\ {p\text{p}p}_A{=}^A{T\text{T}T}_C{\cdot }^C{T\text{T}T}_B\cdot {p\text{p}p}_B{=}^A{T\text{T}T}_B\cdot {p\text{p}p}_B\text{\hspace{1em}(2-2)} \end{gathered}$$
上式中，${}^A{T\text{T}T}_B{=}^A{T\text{T}T}_C{\cdot }^C{T\text{T}T}_B$，表示从A系旋转到B系的旋转矩阵
总的来说，旋转运动是通过旋转矩阵来描述的。

2.3 一般运动

在上图中，$B$系可由$A$系先旋转再平移得到，令${q\text{q}q}_b$表示$B$系中$q$点的坐标，${q\text{q}q}_a$表示$q$在$A$系中的坐标，根据前两节的知识，有：

$${q\text{q}q}_a={p\text{p}p}_{ab}{+}^A{T\text{T}T}_B\cdot {q\text{q}q}_b\text{\hspace{1em}(2-3)}$$

将上式表示成矩阵形式，有：
$$\left[\begin{array}{c}{q\text{q}q}_a\\ 1\end{array}\right]=\left[\begin{array}{cc}{}^A{T\text{T}T}_B& {p\text{p}p}_{ab}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{q\text{q}q}_b\\ 1\end{array}\right]\text{\hspace{1em}(2-4)}$$
即：
$${\overline{q\text{q}q}}_a{=}^a{\overline{g\text{g}g}}_b\cdot {\overline{q\text{q}q}}_b\text{\hspace{1em}(2-5)}$$

上式中，${\overline{q\text{q}q}}_a={\left[\begin{array}{cc}{q\text{q}q}_a& 1\end{array}\right]}^{\mathbf{T}}$，${\overline{q\text{q}q}}_b={\left[\begin{array}{cc}{q\text{q}q}_b& 1\end{array}\right]}^{\mathbf{T}}$，${}^a{\overline{g\text{g}g}}_b$表示从$A$系到$B$系的齐次矩阵，同时包含了旋转运动与平移运动。

三、旋量初识

3.1 概念引入

考虑图2.5(a)中的单连杆机构在参考坐标系中运动，$q$为旋转轴上的一点，$p$为连杆上的一点，绕单位角速度$\omega \text{ω}\omega$($\omega \text{ω}\omega \in {\mathbb{R}}^3$，且$\Vert \omega \text{ω}\omega \Vert =1$)做旋转运动。我们知道，角速度方向的确定方法是：遵循右手法则，四指指向运动方向，大拇指指向即角速度方向。因此，在图2.5(a)中，令$p\text{p}p(t)$表示 $p$ 点 $t$ 时刻在参考坐标系中的坐标，$q\text{q}q$表示$q$点在参考坐标系中的坐标，则$pq=p\text{p}p(t)-q\text{q}q$。因此，根据向量积的物理意义，有$p$点的线速度为：

$$\dot{p}\text{p˙}\dot{p}(t)=\omega \text{ω}\omega \times (p\text{p}p(t)-q\text{q}q)\text{\hspace{1em}(3-1)}$$
令$v\text{v}v=-\omega \text{ω}\omega \times q\text{q}q$，上式可以写为矩阵形式：

$$\left[\begin{array}{c}\dot{p}\text{p˙}\dot{p}\\ 0\end{array}\right]=\left[\begin{array}{cc}\hat{\omega }\text{ω^}\hat{\omega }& v\text{v}v\\ 0& 0\end{array}\right]\left[\begin{array}{c}p\text{p}p\\ 1\end{array}\right]=\hat{\xi }\text{ξ^}\hat{\xi }\left[\begin{array}{c}p\text{p}p\\ 1\end{array}\right]\text{\hspace{1em}(3-2)}$$

式(3-2)中，$\hat{\omega }\text{ω^}\hat{\omega }$ 表示 $\omega \text{ω}\omega$ 的反对称矩阵。

在图2.5(b)中，整个单连杆机构以单位速度$v\text{v}v$做平移运动，那么 $p$ 点的速度为：

$$\dot{p}\text{p˙}\dot{p}(t)=v\text{v}v\text{\hspace{1em}(3-3)}$$

同样将上式写成矩阵形式，有：
$$\left[\begin{array}{c}\dot{p}\text{p˙}\dot{p}\\ 0\end{array}\right]=\left[\begin{array}{cc}0& v\text{v}v\\ 0& 0\end{array}\right]\left[\begin{array}{c}p\text{p}p\\ 1\end{array}\right]={\hat{\xi }\text{ξ^}\hat{\xi }}_v\left[\begin{array}{c}p\text{p}p\\ 1\end{array}\right]\text{\hspace{1em}(3-4)}$$

对比式(3-2)和式(3-4)，可以看出，对于平移运动，有$\omega \text{ω}\omega =0\text{0}0$，则有$\hat{\xi }\text{ξ^}\hat{\xi }={\hat{\xi }\text{ξ^}\hat{\xi }}_v$。因此，我们可以用式(3-5)所示的齐次矩阵同时表示旋转运动与平移运动。

$$\hat{\xi }\text{ξ^}\hat{\xi }=\left[\begin{array}{cc}\hat{\omega }\text{ω^}\hat{\omega }& v\text{v}v\\ 0& 0\end{array}\right]\text{\hspace{1em}(3-5)}$$

因此，我们可以用微分方程来描述上述运动：

$$\dot{\overline{p\text{p}p}}=\hat{\xi }\text{ξ^}\hat{\xi }\overline{p\text{p}p}\text{\hspace{1em}(3-6)}$$

式(3-6)中，$\dot{\overline{p\text{p}p}}={\left[\begin{array}{cc}\dot{p\text{p}p}& 0\end{array}\right]}^{\mathbf{T}}$，$\overline{p\text{p}p}={\left[\begin{array}{cc}p\text{p}p& 1\end{array}\right]}^{\mathbf{T}}$。
求解上述微分方程，得：
$$\overline{p\text{p}p}(t)=e^{\hat{\xi }\text{ξ^}\hat{\xi }t}\overline{p\text{p}p}(0)\text{\hspace{1em}(3-7)}$$

式(3-7)中，$\overline{p\text{p}p}(0)$是 $\overline{p\text{p}p}(t)$ 在零时刻的值。上式中，矩阵$\hat{\xi }\text{ξ^}\hat{\xi }$的指数函数如式(3-8)所示。

$$e^{\hat{\xi }\text{ξ^}\hat{\xi }t}=I\text{I}I+\hat{\xi }\text{ξ^}\hat{\xi }t+\frac{(\hat{\xi }\text{ξ^}\hat{\xi }t{)}^2}{2!}+\frac{(\hat{\xi }\text{ξ^}\hat{\xi }t{)}^3}{3!}+\cdots \text{\hspace{1em}(3-8)}$$

因为$\omega \text{ω}\omega$是单位角速度，因此 $\theta =t$，因此有

$$e^{\hat{\xi }\text{ξ^}\hat{\xi }t}=e^{\hat{\xi }\text{ξ^}\hat{\xi }\theta }\text{\hspace{1em}(3-9)}$$

因此，$e^{\hat{\xi }\text{ξ^}\hat{\xi }\theta }$是一点从起始位置到旋转 $\theta$ 弧度后的位置的变换。

定义六维向量$\xi \text{ξ}\xi =(v\text{v}v,\omega \text{ω}\omega )$表示 $\hat{\xi }\text{ξ^}\hat{\xi }$ 的速度旋量(twist)，运算规则是：

$${\left[\begin{array}{cc}\hat{\omega }\text{ω^}\hat{\omega }& v\text{v}v\\ 0& 0\end{array}\right]}^{\vee }=\left[\begin{array}{c}v\text{v}v\\ \omega \text{ω}\omega \end{array}\right]\text{\hspace{1em}(3-10)}$$

OK，到目前为止，总算是引出了旋量[^1]的概念。

3.2 旋量运动

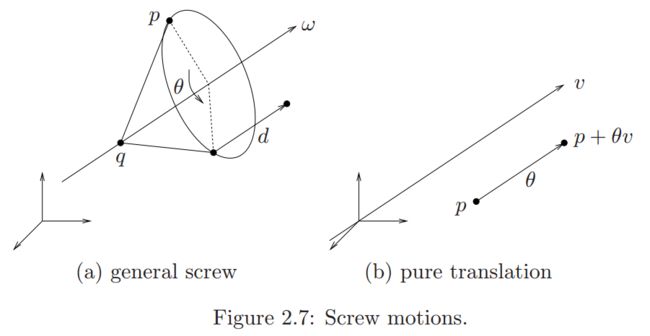
3.1节只是引出了旋量的概念，但是3.1节只是描述了旋转运动与平移运动，如果是旋转加平移呢？图2.7(a)给出了一种类型的刚体运动：先绕空间旋转轴转过 $\theta$ 角，再沿该轴平移距离 $d$ 的刚体运动。这种组合运动称为旋量运动(screw motion)。为了进一步分析方便，我们再定义一个概念，称为旋量的节距$h$，如式(3-7)所示。

$$h=\frac{{\omega \text{ω}\omega }^{\mathbf{T}}{v\text{v}v}_d}{{\Vert \omega \text{ω}\omega \Vert }^2}\text{\hspace{1em}(3-11)}$$

从上式可以看出，$h$ 是平动速度和角速度的比，表示的是平动与转动的比。

对于式(3-7)，我们分两种情况来讨论：
1.当 $\omega \text{ω}\omega =0\text{0}0$时，认为节距无穷大，这时只有平移运动，如图2.7(b)所示。因为旋转角度为0，故把过原点方向为$v\text{v}v$的直线作为旋转轴($v\text{v}v$为一单位矢量)。这时规定，旋量节距为$\infty$，大小为沿$v\text{v}v$方向的移动量。
2.当 $\omega \text{ω}\omega \ne 0\text{0}0$时，要求 $\Vert \omega \text{ω}\omega \Vert =1$，$v\text{v}v=-\omega \text{ω}\omega \times q\text{q}q+h\omega \text{ω}\omega$。$v\text{v}v$为什么是这样的形式呢？类比式(3-1)，同时考虑旋转运动和平动，那么可以有：
$$\dot{p}\text{p˙}\dot{p}(t)=\omega \text{ω}\omega \times (p\text{p}p(t)-q\text{q}q)+h\omega \text{ω}\omega \text{\hspace{1em}(3-12)}$$

同样将其写成矩阵形式，则有：

$$\left[\begin{array}{c}\dot{p}\text{p˙}\dot{p}\\ 0\end{array}\right]=\left[\begin{array}{cc}\hat{\omega }\text{ω^}\hat{\omega }& v\text{v}v\\ 0& 0\end{array}\right]\left[\begin{array}{c}p\text{p}p\\ 1\end{array}\right]=\hat{\xi }\text{ξ^}\hat{\xi }\left[\begin{array}{c}p\text{p}p\\ 1\end{array}\right]\text{\hspace{1em}(3-13)}$$
上式中，$v\text{v}v=-\omega \text{ω}\omega \times q\text{q}q+h\omega \text{ω}\omega$，$v\text{v}v$ 由两部分组成，$-\omega \text{ω}\omega \times q\text{q}q$是旋转引起的线速度，$h\omega \text{ω}\omega$ 是由平动引起的速度。解上述的微分方程可以得到 $p$ 点的位置。

综上所述，由旋转轴上的一点$q$的坐标，单位角速度$\omega \text{ω}\omega$，以及节距 $h$，即可确定旋量$\xi \text{ξ}\xi =(v\text{v}v,\omega \text{ω}\omega )$。

参考文献

1. A mathematical Introduction to robotics manupilation
2. MODERN ROBOTICS MECHANICS, PLANNING, AND CONTROL