Tensorflow2.0学习率衰减详细汇总
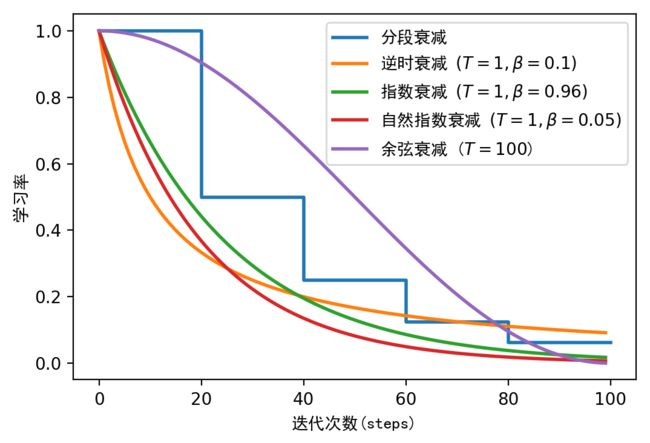
这里先列出5种常见学习率衰减策略的总结,之后详细介绍如何利用tensorflow库自带的类实现学习率衰减。
最后以上面5个例子演示如何自己自定义一个学习率衰减策略。这样大家以后就可以按照自己的需要定制一个学习率调度器了。
学习率调度器的实现参考:
- https://nndl.github.io/ 《神经网络与深度学习》第7章,作者:邱锡鹏
- tensorflow官方API
1. 总结
α 0 \alpha_{0} α0——初始学习率
α t \alpha_{t} αt——第 t t t个step时的学习率
β \beta β ——学习率衰减系数
t t t ——当前是第几个step
T T T ——经历个多少个step后完成一次学习率衰减
这里的公式与《神经网络与深度学习》第7章略微有一点区别,就是引入了 T T T,主要是为了与tensorflow的API相契合。不影响理解。
| 方法 | 公式 | 说明 |
|---|---|---|
| 分段常数衰减 Piecewise Constant Decay |
每经过 T 1 , T 2 , . . . , T m T_1, T_2, ... ,T_m T1,T2,...,Tm倍,学习率就下降为原来的 β 1 , β 2 , . . . , β m \beta_1, \beta_2, ... ,\beta_m β1,β2,...,βm倍 | |
| 逆时衰减 Inverse Time Decay |
α t = α 0 1 1 + β × t T \alpha_{t}=\alpha_{0} \frac{1}{1+\beta \times \frac{t}{T}} αt=α01+β×Tt1 | 经过 T T T个step后,学习率下降为原来的 1 1 + β \frac{1}{1+\beta} 1+β1倍 |
| 指数衰减 Exponential Decay |
α t = α 0 β t T \alpha_{t}=\alpha_{0}\beta^{\frac{t}{T}} αt=α0βTt | 迭代 T T T个step后,学习率降为原来的 β \beta β倍 |
| 自然指数衰减 Natural Exponential Decay |
α t = α 0 exp ( − β × t T ) \alpha_{t}=\alpha_{0} \exp (-\beta \times \frac{t}{T}) αt=α0exp(−β×Tt) | 迭代 T T T个step后,学习率降为原来的 exp ( − β ) \exp{(-\beta)} exp(−β)倍 |
| 余弦衰减 Cosine Decay |
α t = 1 2 α 0 ( 1 + cos ( t π T ) ) \alpha_{t}=\frac{1}{2} \alpha_{0}\left(1+\cos \left(\frac{t \pi}{T}\right)\right) αt=21α0(1+cos(Ttπ)) | 迭代 T T T个step后学习率降至0 |
2. 利用TensorFlow2的API使用学习率衰减
下面通过tensorflow2的API演示如何创建一个学习率衰减调度器,以下例子中的初始学习率均为 α 0 = 1 \alpha_0=1 α0=1。
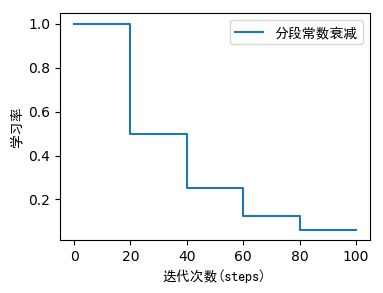
2.1 分段常数衰减(Piecewise Constant Decay)
# 分段常数衰减(Piecewise Constant Decay)
import tensorflow as tf
boundaries=[20, 40, 60, 80] # 以 0-20 20-40 40-60 60-80 80-inf 为分段
values=[1, 0.5, 0.25, 0.125, 0.0625] # 各个分段学习率的值
piece_wise_constant_decay = tf.keras.optimizers.schedules.PiecewiseConstantDecay(
boundaries=boundaries, values=values, name=None)
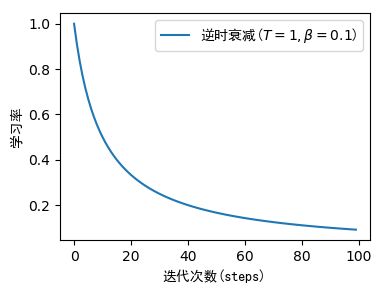
2.2 逆时衰减(Inverse Time Decay)
α t = α 0 1 1 + β × t T \alpha_{t}=\alpha_{0} \frac{1}{1+\beta \times \frac{t}{T}} αt=α01+β×Tt1
initial_learning_rate=1.相当于 α 0 = 1 \alpha_0= 1 α0=1
decay_steps=1相当于 T = 1 T=1 T=1
decay_rate=0.1相当于 β = 0.1 \beta=0.1 β=0.1
即:
α t = 1 ⋅ 1 1 + 0.1 t \alpha_{t}=1 · \frac{1}{1+0.1t} αt=1⋅1+0.1t1
import tensorflow as tf
inverse_time_decay = tf.keras.optimizers.schedules.InverseTimeDecay(
initial_learning_rate=1., decay_steps=1, decay_rate=0.1)
2.3 指数衰减(Exponential Decay)
α t = α 0 β t T \alpha_{t}=\alpha_{0}\beta^{\frac{t}{T}} αt=α0βTt
initial_learning_rate=1.相当于 α 0 = 1 \alpha_0= 1 α0=1
decay_steps=1相当于 T = 1 T=1 T=1
decay_rate=0.96相当于 β = 0.96 \beta=0.96 β=0.96
即:
α t = 1 ⋅ 0.9 6 t \alpha_{t}=1·0.96^{t} αt=1⋅0.96t
import tensorflow as tf
exponential_decay = tf.keras.optimizers.schedules.ExponentialDecay(
initial_learning_rate=1., decay_steps=1, decay_rate=0.96)
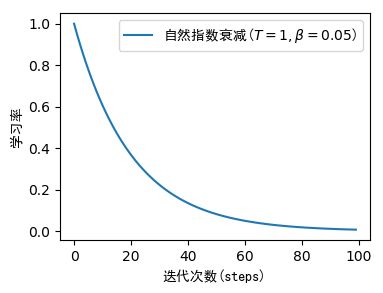
2.4 自然指数衰减(Natural Exponential Decay)
α t = α 0 exp ( − β × t T ) \alpha_{t}=\alpha_{0} \exp (-\beta \times \frac{t}{T}) αt=α0exp(−β×Tt)
initial_learning_rate=1.相当于 α 0 = 1 \alpha_0= 1 α0=1
decay_steps=1相当于 T = 1 T=1 T=1
decay_rate=0.96相当于 β = 0.05 \beta=0.05 β=0.05
即:
α t = 1 ⋅ exp ( − 0.05 t ) \alpha_{t}=1·\exp (-0.05t) αt=1⋅exp(−0.05t)
这个实现方案我没在tensorflow找到,于是自己实现了一个,这部分如果不太理解,可以暂时跳过这部分。自定义学习率调度器的方法在后面有提到。
import tensorflow as tf
class NaturalExpDecay(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, initial_learning_rate, decay_steps, decay_rate):
super().__init__()
self.initial_learning_rate = tf.cast(initial_learning_rate, dtype=tf.float32)
self.decay_steps = tf.cast(decay_steps, dtype=tf.float32)
self.decay_rate = tf.cast(decay_rate, dtype=tf.float32)
def __call__(self, step):
return self.initial_learning_rate * tf.math.exp(-self.decay_rate * (step / self.decay_steps))
natural_exp_decay = NaturalExpDecay(initial_learning_rate=1,
decay_steps=1,
decay_rate=0.05)
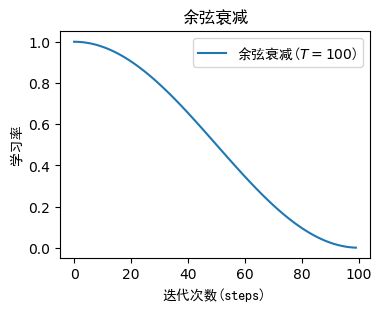
2.5 余弦衰减(Cosine Decay)
α t = 1 2 α 0 ( 1 + cos ( t π T ) ) \alpha_{t}=\frac{1}{2} \alpha_{0}\left(1+\cos \left(\frac{t \pi}{T}\right)\right) αt=21α0(1+cos(Ttπ))
initial_learning_rate=1.相当于 α 0 = 1 \alpha_0= 1 α0=1
decay_steps=100相当于 T = 100 T=100 T=100
即:
α t = 1 2 ⋅ 1 ⋅ ( 1 + cos ( t π 100 ) ) \alpha_{t}=\frac{1}{2} ·1·\left(1+\cos \left(\frac{t \pi}{100}\right)\right) αt=21⋅1⋅(1+cos(100tπ))
注意这里 T = 100 T=100 T=100而不是1,当 t = 100 t=100 t=100时, α t = 0.5 ⋅ ( 1 + c o s ( π ) ) = 0.5 ⋅ ( 1 − 1 ) = 0 \alpha_t=0.5·(1+cos(\pi))=0.5·(1-1)=0 αt=0.5⋅(1+cos(π))=0.5⋅(1−1)=0
import tensorflow as tf
cosine_decay = tf.keras.experimental.CosineDecay(
initial_learning_rate=1., decay_steps=100)
2.6 使用方法
学习率衰减调度器的使用方法非常简单,以指数衰减为例。
- 先创建一个学习率衰减调度器
- 把它传入你选择的优化器(这里选择Adam优化器)
import tensorflow as tf
# 1. 先创建指数衰减学习率
exponential_decay = tf.keras.optimizers.schedules.ExponentialDecay(
initial_learning_rate=0.01, decay_steps=1000, decay_rate=0.96)
# 2. 送入优化器
optimizer = tf.keras.optimizers.Adam(exponential_decay)
# 普通的优化器
# optimizer = tf.keras.optimizers.Adam(0.01)
3. 自定义实现学习率衰减
这部分参考了tensorflow教程里有关自定义学习率的部分。
通过参考下面的例子,大家以后就可以自由的定义自己需要的学习率调度器。实现学习率衰减,warmup等功能。
首先需要创建一个自定义学习率调度器的类,继承tf.keras.optimizers.schedules.LearningRateSchedule
创建好后,使用方法与2.6完全一致。
代码如下
分段常数衰减(Piecewise Constant Decay)
import tensorflow as tf
class PiecewiseConstantDecay(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, boundaries, values):
super().__init__()
self.boundaries = tf.cast(boundaries, dtype=tf.float32)
self.values = tf.cast(values, dtype=tf.float32)
def __call__(self, step):
for i in range(len(self.boundaries)):
if self.boundaries[i] >= step:
return self.values[i]
else:
return self.values[-1]
逆时衰减(Inverse Time Decay)
import tensorflow as tf
class InverseTimeDecay(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, initial_learning_rate, decay_steps, decay_rate):
super().__init__()
self.initial_learning_rate = tf.convert_to_tensor(initial_learning_rate)
self.decay_steps = tf.cast(decay_steps, dtype=tf.float32)
self.decay_rate = tf.convert_to_tensor(decay_rate)
def __call__(self, step):
step = tf.convert_to_tensor(step)
return self.initial_learning_rate / (1 + self.decay_rate * step / self.decay_steps)
指数衰减(Exponential Decay)
import tensorflow as tf
class ExponentialDecay(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, initial_learning_rate, decay_steps, decay_rate):
super().__init__()
self.initial_learning_rate = tf.cast(initial_learning_rate, dtype=tf.float32)
self.decay_steps = tf.cast(decay_steps, dtype=tf.float32)
self.decay_rate = tf.cast(decay_rate, dtype=tf.float32)
def __call__(self, step):
return self.initial_learning_rate * self.decay_rate ** (step / self.decay_steps)
余弦衰减(Cosine Decay)
import tensorflow as tf
from math import pi
class CosineDecay(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, initial_learning_rate, decay_steps):
super().__init__()
self.initial_learning_rate = tf.cast(initial_learning_rate, dtype=tf.float32)
self.decay_steps = tf.cast(decay_steps, dtype=tf.float32)
def __call__(self, step):
return self.initial_learning_rate * (1 + tf.math.cos(step * pi / self.decay_steps)) / 2