11_Training Deep Neural Networks_VarianceScaling_leaky relu_PReLU_SELU _Batch Normalization_Reusing

     In Cp10 (https://blog.csdn.net/Linli522362242/article/details/106433059) we introduced artificial neural networks and trained our first deep neural networks. But they were shallow nets, with just a few hidden layers. What if you need to tackle a complex problem, such as detecting hundreds of types of objects in high-resolution images? You may need to train a much deeper DNN, perhaps with 10 layers or many more, each containing hundreds of neurons, linked by hundreds of thousands of connections. Training a deep DNN isn’t a walk in the park. Here are some of the problems you could run into:

• You may be faced with the tricky vanishing消失了 gradients problem or the related exploding gradients problem. This is when the gradients grow smaller and smaller, or larger and larger, when flowing backward through the DNN during training. Both of these problems make lower layers very hard to train.
   
• You might not have enough training data for such a large network, or it might be too costly to label.
   
• Training may be extremely slow.
   
• A model with millions of parameters would severely risk overfitting the training set, especially if there are not enough training instances or if they are too noisy.

     Here, we will go through each of these problems and present techniques to solve them. We will start by exploring the vanishing and exploding gradients problems and some of their most popular solutions. Next, we will look at transfer learning and unsupervised pretraining, which can help you tackle complex tasks even when you have little labeled data. Then we will discuss various optimizers that can speed up training large models tremendously. Finally, we will go through a few popular regularization
techniques for large neural networks.

With these tools, you will be able to train very deep nets. Welcome to Deep Learning!

The Vanishing/Exploding Gradients Problems

     As we discussed in Chapter 10, the backpropagation algorithm works by going from the output layer to the input layer, propagating the error gradient along the way. Once the algorithm has computed the gradient of the cost function with regard to each parameter in the network, it uses these gradients to update each parameter with a Gradient Descent step.

     Unfortunately, gradients often get smaller and smaller as the algorithm progresses down to the lower layers. As a result, the Gradient Descent update leaves the lower layers’ connection weights virtually unchanged, and training never converges to a good solution. We call this the vanishing gradients problem. In some cases, the opposite can happen: the gradients can grow bigger and bigger until layers get insanely large weight updates and the algorithm diverges. This is the exploding gradients problem, which surfaces in recurrent neural networks (see Chapter 15). More generally, deep neural networks suffer from unstable gradients; different layers may learn at widely different speeds.

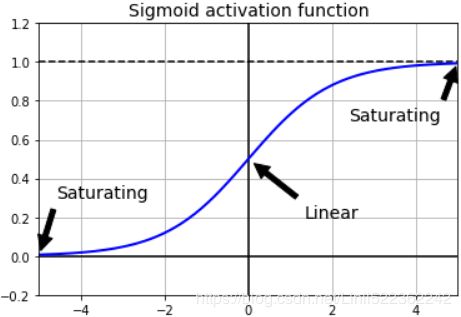
     This unfortunate behavior was empirically[ɪm'pɪrɪklɪ]以经验为主地; observed long ago, and it was one of the reasons deep neural networks were mostly abandoned in the early 2000s. It wasn’t clear what caused the gradients to be so unstable when training a DNN, but some light was shed in a 2010 paper by Xavier Glorot and Yoshua Bengio. The authors found a few suspects, including the combination of the popular logistic sigmoid activation function and the weight initialization technique that was most popular at the time (i.e., a normal distribution with a mean of 0 and a standard deviation of 1). In short, they showed that with this activation function and this initialization scheme, the variance of the outputs of each layer is much greater than the variance of its inputs. Going forward in the network, the variance keeps increasing after each layer until the activation function saturates at the top layers. This saturation is actually made worse by the fact that the logistic function has a mean of 0.5, not 0 (the hyperbolic tangent function has a mean of 0 and behaves slightly better than the logistic function in deep networks).

     Looking at the logistic activation function (see Figure 11-1), you can see that when inputs become large (negative or positive), the function saturates at 0 or 1, with a derivative extremely close to 0. Thus, when backpropagation kicks in it has virtually几乎 no gradient to propagate back through the network; and what little gradient exists keeps getting diluted稀释 as backpropagation progresses down through the top layers, so there is really nothing left for the lower layers.

import numpy as np
import matplotlib.pyplot as plt

def logit(z):
    return 1/( 1+np.exp(-z) )

z = np.linspace(-5, 5, 200)

plt.plot( [-5,5],[0,0], 'k-' ) #x-axis
plt.plot( [-5,5],[1,1], 'k--') #x=1
plt.plot( [0,0], [-0.2, 1.2], 'k-') #y-axis
plt.plot(z, logit(z), 'b-', linewidth=2)
props = dict( facecolor='black', shrink=0.1)
plt.annotate("Saturating", xytext=(3.5,0.7), 
             xy=(5,1), arrowprops=props, 
             fontsize=14, ha='center'
            )
plt.annotate('Saturating', xytext=(-3.5, 0.3), 
             xy=(-5,0), arrowprops=props, 
             fontsize=14, ha='center'
            )
plt.annotate('Linear', xytext=(2,0.2),
             xy=(0,0.5), arrowprops=props,
             fontsize=14, ha='center'
            )
plt.grid(True)
plt.title('Sigmoid activation function', fontsize=14)
plt.axis([-5,5, -0.2, 1.2])

plt.show()

Figure 11-1. Logistic activation function saturation 

Xavier(Glorot) and He Initialization

     In their paper, Glorot and Bengio propose a way to significantly alleviate[əˈliːvieɪt]减轻 this problem. We need the signal to flow properly in both directions: in the forward direction when making predictions, and in the reverse direction when backpropagating gradients. We don’t want the signal to die out消失, nor do we want it to explode and saturate. For the signal to flow properly, the authors argue that we need the variance of the outputs of each layer to be equal to the variance of its inputs, and we also need the gradients to have equal variance before and after flowing through a layer in the reverse direction (please check out the paper if you are interested in the mathematical details). It is actually not possible to guarantee both unless the layer has an equal number of input and output connections, but they proposed a good compromise妥协 that has proven to work very well in practice: the connection weights must be initialized randomly as described in Equation 11-1, where and are the number of input and output connections for the layer whose weights are being initialized (also called fan-in and fan-out; ). This initialization strategy is often called Xavier initialization (after the author’s first name), or sometimes Glorot initialization.

Equation 11-1. Xavier initialization (when using the logistic activation function)

Normal distribution with mean 0 and standard deviation 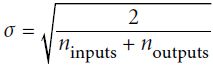OR 

Or a uniform distribution between ‐r and +r, with 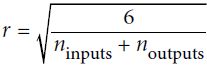 OR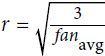 

     If you replace with in Equation 11-1, you get an initialization strategy that Yann LeCun proposed in the 1990s. He called it LeCun initialization. Genevieve Orr and Klaus-Robert Müller even recommended it in their 1998 book Neural Networks: Tricks of the Trade (Springer). LeCun initialization is equivalent to Glorot initialization when . It took over a decade for researchers to realize how important this trick is. Using Glorot initialization can speed up training considerably, and it is one of the tricks that led to the success of Deep Learning.

     When the number of input connections is roughly equal to the number of output connections, you get simpler equations (e.g., ). We used this simplified strategy in Cp10.3 https://blog.csdn.net/Linli522362242/article/details/106562190

import numpy as np
 
#inputs, the number of neurons, the name of the layer, the activation function
def neuron_layer( X, n_neurons, name, activation=None):
    with tf.name_scope(name):
        n_inputs = int( X.get_shape()[1] ) # X.get_shape()[1] : the number of features
        
        stddev = 2 / np.sqrt( n_inputs )
                                       # shape
        init = tf.truncated_normal( (n_inputs, n_neurons), stddev=stddev )
        # truncated_normal( shape, mean=0.0, stdev=1.0 ) # range: [ mean-2*stddev, mean+2*stddev ]
        # stddev=stddev ==> stddev= 2/np.sqrt( n_inputs ) ==> range: mean += 2* 2/np.sqrt( n_inputs )
        # 截断的产生正态分布的随机数，即随机数与均值的差值若大于两倍的标准差，则重新生成 |x-mean| <=2*stddev
        W = tf.Variable(init, name="kernel")                # W.shape: (features, n_neurons)
        b = tf.Variable(tf.zeros([n_neurons]), name="bias")
        Z = tf.matmul( X,W) # X dot W # prediction          # X.shape(): (instances, features)  
                                                            # X dot W ==> Z.shape(instances, n_neurons) 
        if activation is not None:
            return activation(Z)
        else:
            return Z

     Using the Xavier initialization strategy can speed up training considerably相当, and it is one of the tricks that led to the current success of Deep Learning. Some recent papers have provided similar strategies for different activation functions, as shown in Table 11-1(for the uniform distribution, just compute r =<==). The initialization strategy for the ReLU activation function (and its variants, including the ELU activation described shortly) is sometimes called He initialization (after the last name of its author). The SELU activation function will be explained later in this chapter. It should be used with LeCun initialization (preferably with a normal distribution, as we will see).

Table 11-1. Initialization parameters for each type of activation function
 OR

from tensorflow.contrib.layers import fully_connected
 
with tf.name_scope("dnn"):
    hidden1 = fully_connected(X, n_hidden1, scope="hidden1")
    hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2")
    logits = fully_connected(hidden2, n_outputs, scope="outputs", activation_fn=None)

By default, the fully_connected() function (introduced in Cp10 https://blog.csdn.net/Linli522362242/article/details/106433059) uses Xavier initialization (with a uniform distribution). You can change this to He initialization by using the variance_scaling_initializer() function like this:

from tensorflow import keras

[name for name in dir(keras.initializers) if not name.startswith("_")]

['Constant',
 'GlorotNormal',
 'GlorotUniform',
 'Identity',
 'Initializer',
 'Ones',
 'Orthogonal',
 'RandomNormal',
 'RandomUniform',
 'TruncatedNormal',
 'VarianceScaling',
 'Zeros',
 'constant',
 'deserialize',
 'get',
 'glorot_normal',
 'glorot_uniform',
 'he_normal',
 'he_uniform',
 'identity',
 'lecun_normal',
 'lecun_uniform',
 'ones',
 'orthogonal',
 'serialize',
 'zeros']

By default, Keras uses Glorot initialization with a uniform distribution. When creating a layer, you can change this to He initialization by setting kernel_initializer="he_uniform" or kernel_initializer="he_normal" like this:

keras.layers.Dense(10, activation='relu', kernel_initializer="he_normal")

     If you want He initialization with a uniform distribution but based on rather than , you can use the VarianceScaling initializer like this:

VarianceScaling class

https://keras.io/api/layers/initializers/

Arguments

• scale: Scaling factor (positive float).
• mode: One of "fan_in", "fan_out", "fan_avg".
• distribution: Random distribution to use. One of "truncated_normal", "untruncated_normal" and "uniform".
• seed: A Python integer. An initializer created with a given seed will always produce the same random tensor for a given shape and dtype.

     With distribution="truncated_normal" or "untruncated_normal", samples are drawn from a truncated/untruncated normal distribution with a mean of zero and a standard deviation (after truncation, if used) stddev = sqrt(scale / n), where n is:

• number of input units in the weight tensor, if mode="fan_in"
• number of output units, if mode="fan_out"
• average of the numbers of input and output units, if mode="fan_avg"

     With distribution="uniform", samples are drawn from a uniform distribution within [-limit, limit], where limit = sqrt(3 * scale / n)==sqrt(scale) * sqrt(3/n).

For example: Uniform distribution
 ==> mode="fan_avg" and scale=2

init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg', 
                                          distribution='uniform')
keras.layers.Dense(10, activation='relu', kernel_initializer=init)

Nonsaturating Activation Functions

     One of the insights in the 2010 paper by Glorot and Bengio was that the problems with unstable gradients were in part due to a poor choice of activation function. Until then most people had assumed that if Mother Nature had chosen to use roughly sigmoid activation functions in biological neurons, they must be an excellent choice. But it turns out that other activation functions behave much better in deep neural networks—in particular, the ReLU activation function, mostly because it does not saturate for positive values (and because it is fast to compute).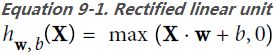

     Unfortunately, the ReLU activation function is not perfect. It suffers from a problem known as the dying ReLUs: during training, some neurons effectively “die,” meaning they stop outputting anything other than 0. In some cases, you may find that half of your network’s neurons are dead, especially if you used a large learning rate. A neuron dies when its weights get tweaked in such a way that the weighted sum of its inputs are negative for all instances in the training set. When this happens, it just keeps outputting zeros, and Gradient Descent does not affect it anymore because the gradient of the ReLU function is zero when its input is negative.

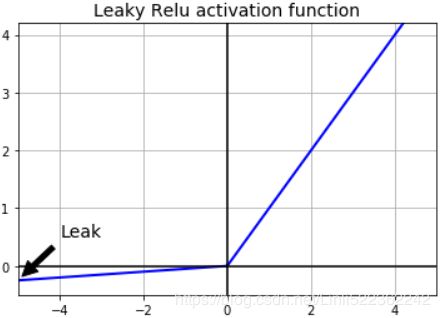
     To solve this problem, you may want to use a variant of the ReLU function, such as the leaky ReLU. This function is defined as LeakyReLUα(z) = max(αz, z) (see Figure 11-2). The hyperparameter α defines how much the function “leaks”泄漏: it is the slope of the function for z < 0 and is typically set to 0.01. This small slope ensures that leaky ReLUs never die; they can go into a long coma怠惰/昏迷, but they have a chance to eventually wake up. A 2015 paper compared several variants of the ReLU activation function, and one of its conclusions was that the leaky variants always outperformed the strict ReLU activation function. In fact, setting α = 0.2 (a huge leak) seemed to result in better performance than α = 0.01 (a small leak). The paper also evaluated the randomized leaky ReLU (RReLU), where α is picked randomly in a given range during training and is fixed to an average value during testing. RReLU also performed fairly well and seemed to act as a regularizer (reducing the risk of overfitting the training set). Finally, the paper evaluated the parametric参（变）数的 leaky ReLU (PReLU), where α is authorized to be learned during training (instead of being a hyperparameter, it becomes a parameter that can be modified by backpropagation like any other parameter). PReLU was reported to strongly outperform ReLU on large image datasets, but on smaller datasets it runs the risk of overfitting the training set.

def leaky_relu(z, alpha=0.01):
    return np.maximum(alpha*z, z) #z = np.linspace(-5, 5, 200)

plt.plot(z, leaky_relu(z,0.05), "b-", linewidth=2)
plt.plot( [-5, 5], [0,0], 'k-' ) # x-axis
plt.plot( [0,0], [-0.5, 4.2], 'k-' ) # y-axis
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5),
             xy=(-5,-0.25), #since leaky_relu(-5,0.05)==-0.25
             arrowprops=props,
             fontsize=14, ha='center'
            )
plt.title('Leaky Relu activation function', fontsize=14)
plt.axis([-5,5, -0.5,4.2])

plt.show()

Figure 11-2. Leaky ReLU: like ReLU, but with a small slope for negative values 

     Last but not least, a 2015 paper by Djork-Arné Clevert et al. proposed a new activation function called the exponential linear unit (ELU) that outperformed all the ReLU variants in the authors’ experiments: training time was reduced, and the neural network performed better on the test set. Figure 11-3 graphs the function, and Equation 11-2 shows its definition.

Equation 11-2. ELU activation function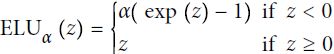

def elu(z, alpha=0.01):
    return np.where(z<0,alpha*(np.exp(z)-1), z)
             ###alpha=1
plt.plot(z, elu(z,1), "b-", linewidth=2)
plt.plot( [-5, 5], [0,0], 'k-' ) # x-axis
plt.plot( [-5, 5], [-1,-1], 'k--')
plt.plot( [0,0], [-1.5, 4.2], 'k-' ) # y-axis
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5),
             xy=(-5,-1), #since min(elu(z,1))==-0.9932620530009145
             arrowprops=props,
             fontsize=14, ha='center'
            )
plt.title('Elu activation function $(a=1)$', fontsize=14)
plt.axis([-5,5, -1.5,4.2])

plt.show()

Figure 11-3. ELU activation function 

Implementing ELU in TensorFlow is trivial, just specify the activation function when building each layer:

keras.layers.Dense(10, activation="elu")

The ELU activation function looks a lot like the ReLU function, with a few major differences:

• It takes on negative values when z < 0, which allows the unit to have an average output closer to 0 and helps alleviate the vanishing gradients problem. The hyperparameter α defines the value that the ELU function approaches when z is a large negative number. It is usually set to 1### elu(z,1) ###, but you can tweak it like any other hyperparameter.
• It has a nonzero gradient for z < 0, which avoids the dead neurons problem.
• If α is equal to 1 then the function is smooth everywhere, including around z = 0, which helps speed up Gradient Descent since it does not bounce弹回 as much to the left and right of z = 0.

     The main drawback of the ELU activation function is that it is slower to compute than the ReLU function and its variants (due to the use of the exponential function). Its faster convergence rate during training compensates for that slow computation, but still, at test time an ELU network will be slower than a ReLU network.

    Then, a 2017 paper by Günter Klambauer et al. introduced the Scaled ELU (SELU) activation function: as its name suggests, it is a scaled variant of the ELU activation function. The authors showed that if you build a neural network composed exclusively of a stack of dense layers仅由一叠dense layers组成, and if all hidden layers use the SELU activation function, then the network will self-normalize: the output of each layer will tend to preserve a mean of 0 and standard deviation of 1 during training, which solves the vanishing/exploding gradients problem. As a result, the SELU activation function often significantly outperforms other activation functions for such neural nets (especially deep ones). There are, however, a few conditions for self-normalization to happen (see the paper for the mathematical justification):

• The input features must be standardized (mean 0 and standard deviation 1).
   
• Every hidden layer’s weights must be initialized with LeCun normal initialization. In Keras, this means setting kernel_initializer="lecun_normal".
   
• The network’s architecture must be sequential. Unfortunately, if you try to use SELU in nonsequential architectures, such as recurrent networks (see Chapter15) or networks with skip connections (i.e., connections that skip layers, such as in Wide & Deep nets), self-normalization will not be guaranteed, so SELU will not necessarily outperform other activation functions.
   
• The paper only guarantees self-normalization if all layers are dense, but some researchers have noted that the SELU activation function can improve performance in convolutional neural nets as well (see Chapter 14).

[m for m in dir(keras.layers) if "relu" in m.lower()]

 

#############################################

     So, which activation function should you use for the hidden layers of your deep neural networks? Although your mileage will vary, in general SELU > ELU > leaky ReLU (and its variants) > ReLU > tanh > logistic. If the network’s architecture prevents it from selfnormalizing, then ELU may perform better than SELU (since SELU is not smooth at z = 0). If you care a lot about runtime latency运行时延迟, then you may prefer leaky ReLU. If you don’t want to tweak yet another hyperparameter, you may use the default α values used by Keras (e.g., 0.3 for leaky ReLU, the hyperparameter α defines the value that the ELU function approaches when z is a large negative number.It is usually set to 1). If you have spare time and computing power, you can use cross-validation to evaluate other activation functions, such as RReLU if your network is overfitting or PReLU if you have a huge training set. That said, because ReLU is the most used activation function (by far), many libraries and hardware accelerators provide ReLU-specific optimizations; therefore, if speed is your priority, ReLU might still be the best choice.
#############################################

LeakyReLU

     To use the leaky ReLU activation function, create a LeakyReLU layer and add it to your model just after the layer you want to apply it to:
Let's train a neural network on Fashion MNIST using the LeakyReLUα(z) = max(αz, z) with α=0.3 :

(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
 
# scale the pixel intensities down to the 0–1 range by dividing them by 255.0 
#(this also converts them to floats)
X_train_full = X_train_full/255.0
X_test = X_test/255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]

import tensorflow as tf

tf.random.set_seed(42)
np.random.seed(42)

model = keras.models.Sequential([
    # It is a Flatten layer whose role is to convert each input image into a 1D array
    keras.layers.Flatten( input_shape=[28,28]), #28*28=784

    keras.layers.Dense(300, kernel_initializer='he_normal'), #variance=2/fan_in
    # To use the leaky ReLU activation function, create a LeakyReLU layer and add it to your
    # model just after the layer you want to apply it to:
    keras.layers.LeakyReLU(), #LeakyReLUα(z) = max(αz, z) #keras.layers.LeakyReLU(alpha=0.3, **kwargs)

    keras.layers.Dense(100, kernel_initializer='he_normal'),
    keras.layers.LeakyReLU(), # alpha is the slope of the function for z < 0
    # we add a Dense output layer with 10 neurons (one per class(0~9)), 
    # using the softmax activation function (because the classes are exclusive).
    keras.layers.Dense(10, activation='softmax')
])

model.compile( loss="sparse_categorical_crossentropy",
               optimizer=keras.optimizers.SGD(lr=1e-3),
               # Here, we’ll only care about accuracy score(the fraction of the images that 
               # were correctly classified).
               metrics=['accuracy']
             )

history = model.fit(X_train, y_train, epochs=10,
                    validation_data=(X_valid, y_valid)
                   )

history.params

import pandas as pd
import matplotlib.pyplot as plt
 
colors=[#"blue", "gray", #  loss      accuracy
        "red", "black"] #   val_loss  val_accuracy
                               #df[ ["val_loss","val_accuracy"] ].plot(figsize=(8,5), color=colors)
pd.DataFrame( history.history )[["val_loss","val_accuracy"]].plot(figsize=(8,5), color=colors)

# the validation error is computed at the end of each epoch, while the training error is 
# computed using a running mean during each epoch. So the training curve should be shifted by 
# half an epoch to the left.
#shift(-0.5)
         #1D array                #list
plt.plot(np.arange(-0.5,9,1), history.history["loss"], c="blue", label="loss")    #must be put after previous code for plotting Dataframe
plt.plot(np.arange(-0.5,9,1), history.history["accuracy"], c="gray", label="accuracy")#must be put after previous code for plotting Dataframe
plt.legend()
plt.grid(True)
plt.gca().set_ylim(0,1) # set the vertical range to [0-1]
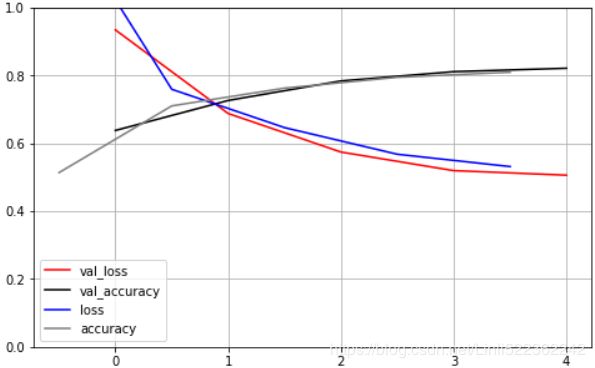
plt.show()

https://blog.csdn.net/Linli522362242/article/details/106562190 

    You can see that both the training accuracy and the validation accuracy steadily increase during training, while the training loss and the validation loss decrease. Good! Moreover, the validation curves are close to the training curves, which means that there is not too much overfitting.  The validation error is computed at the end of each epoch, while the training error is computed using a running mean during each epoch. So the training curve should be shifted by half an epoch to the left. If you do that, you will see that the training and validation curves overlap almost perfectly at the beginning of training.

 

X_new = X_test[:3]

y_pred = model.predict_classes(X_new)
y_pred

model.evaluate( X_test, y_test )

history.history['val_accuracy']

 

     As we saw in Chapter 2, it is common to get slightly lower performance on the test set than on the validation set, because the hyperparameters are tuned on the validation set, not the test set (however, in this example, we did not do any hyperparameter tuning, so the lower accuracy is just bad luck). Remember to resist the temptation to tweak the hyperparameters on the test set, or else your estimate of the generalization error will be too optimistic.

     For PReLU, replace LeakyRelu(alpha=0.2) with PReLU(). There is currently no official implementation of RReLU in Keras, but you can fairly easily implement your own (to learn how to do that, see the exercises at the end of Chapter 12).

PReLU class ()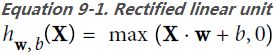

tf.keras.layers.PReLU(
    alpha_initializer="zeros", # Initializer function for the weights.
    alpha_regularizer=None,  # Regularizer for the weights.
    alpha_constraint=None,   # Constraint for the weights.
    shared_axes=None,          # The axes along which to share learnable parameters for the activation function.
                                                # For example, if the incoming feature maps are from a 2D convolution with
                                                # output  shape (batch, height, width, channels), and you wish to share parameters
                                                # across space so that each filter only has one set of parameters, set shared_axes=[1, 2].
    **kwargs
)

tf.random.set_seed(42)
np.random.seed(42)

model = keras.models.Sequential([
    # It is a Flatten layer whose role is to convert each input image into a 1D array
    keras.layers.Flatten( input_shape=[28,28]),

    keras.layers.Dense(300, kernel_initializer="he_normal"),
    # To use the PReLU activation function, create a PReLU layer and add it to your
    # model just after the layer you want to apply it to:
    keras.layers.PReLU(),

    keras.layers.Dense(100, kernel_initializer="he_normal"),
    keras.layers.PReLU(),

    keras.layers.Dense(10, activation="softmax")#handle multiple classes, outputting one probability per class
])

model.compile(loss="sparse_categorical_crossentropy",
              optimizer=keras.optimizers.SGD(lr=1e-3),
              # Here, we’ll only care about accuracy score(the fraction of the images that 
              # were correctly classified).
              metrics=["accuracy"]
             )

history = model.fit( X_train, y_train, epochs=10, validation_data=(X_valid, y_valid) )

 

import pandas as pd
import matplotlib.pyplot as plt
 
colors=[#"blue", "gray", #  loss      accuracy
        "red", "black"] #   val_loss  val_accuracy
                               #df[ ["val_loss","val_accuracy"] ].plot(figsize=(8,5), color=colors)
pd.DataFrame( history.history )[["val_loss","val_accuracy"]].plot(figsize=(8,5), color=colors)

# the validation error is computed at the end of each epoch, while the training error is 
# computed using a running mean during each epoch. So the training curve should be shifted by 
# half an epoch to the left.
#shift(-0.5)
         #1D array                #list
plt.plot(np.arange(-0.5,9,1), history.history["loss"], c="blue", label="loss")    #must be put after previous code for plotting Dataframe
plt.plot(np.arange(-0.5,9,1), history.history["accuracy"], c="gray", label="accuracy")#must be put after previous code for plotting Dataframe
plt.legend()
plt.grid(True)
plt.gca().set_ylim(0,1) # set the vertical range to [0-1]
plt.show()

model.evaluate( X_test, y_test )

history.history['val_accuracy'][-1]

     As we saw in Chapter 2, it is common to get slightly lower performance on the test set than on the validation set, because the hyperparameters are tuned on the validation set, not the test set (however, in this example, we did not do any hyperparameter tuning, so the lower accuracy is just bad luck). Remember to resist the temptation to tweak the hyperparameters on the test set, or else your estimate of the generalization error will be too optimistic.

X_new = X_test[:3]

y_pred = model.predict_classes(X_new)
y_pred

SELU

     This activation function was proposed in this great paper(https://arxiv.org/pdf/1706.02515.pdf) by Günter Klambauer, Thomas Unterthiner and Andreas Mayr, published in June 2017. During training, a neural network composed exclusively of a stack of dense layers using the SELU activation function and LeCun initialization will self-normalize(Every hidden layer’s weights must be initialized with LeCun normal initialization): the output of each layer will tend to preserve the same mean and variance during training, which solves the vanishing/exploding gradients problem. As a result, this activation function outperforms the other activation functions very significantly for such neural nets, so you should really try it out. Unfortunately, the self-normalizing property of the SELU activation function is easily broken: you cannot use ℓ1 or ℓ2 regularization, regular dropout https://blog.csdn.net/Linli522362242/article/details/106755312, max-norm最大范数, skip connections or other non-sequential topologies (so recurrent neural networks won't self-normalize). However, in practice it works quite well with sequential CNNs. If you break self-normalization, SELU will not necessarily outperform other activation functions.(then consider SELU > ELU > leaky ReLU (and its variants) > ReLU > tanh > logistic. )

Error function误差函数https://en.wikipedia.org/wiki/Error_function
     In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as: OR and erf(∞)=1和erf(-x)= - erf(x)。

     This integral is a special (non-elementary) and sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.

     In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and variance 1/2,  erf x is the probability that Y falls in the range[−x, x].

     Two closely related functions are the complementary error function 互补误差函数(erfc) defined as OR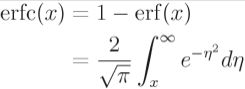

and the imaginary error function (erfi) defined as  where i is the imaginary unit.

paper: https://arxiv.org/pdf/1706.02515.pdf

*

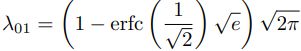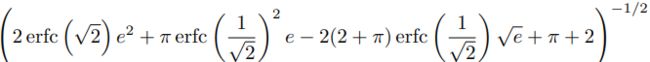
from scipy.special import erfc

# alpha and scale to self normalize with mean 0 and standard deviation 1
# (see equation 14 in the paper https://arxiv.org/pdf/1706.02515.pdf):
alpha_0_1 = -np.sqrt(2/np.pi) / ( erfc(1/np.sqrt(2)) * np.exp(1/2)-1 ) # alpha_0_1 ≈ 1.6732632423543778
scale_0_1 = ( 1- erfc( 1/np.sqrt(2) )*np.sqrt(np.e) ) * np.sqrt( 2*np.pi )*\
            ( 2* erfc( np.sqrt(2) )*np.e**2 + np.pi*erfc(1/np.sqrt(2))**2*np.e \
             -2*(2+np.pi)*erfc( 1/np.sqrt(2) )*np.sqrt(np.e) + np.pi + 2\
            )**(-1/2)  # scale_0_1 ≈ 1.0507009873554805

def selu( z, scale=scale_0_1, alpha=alpha_0_1 ):
    return scale * elu(z,alpha)

plt.plot(z, selu(z), "b-", linewidth=2)
plt.plot([-5,5], [0,0], 'k-') #x-axis
plt.plot([-5,5], [-1.758, -1.758], 'k--') #y=-1.758 since min(selu(-5))=-1.7462533606696207
plt.plot([0,0], [-2.2, 3.2], 'k-')#y-axis
plt.grid(True)
plt.title('SELU activation function')
plt.axis([-5,5, -2.2, 3.2])
plt.show()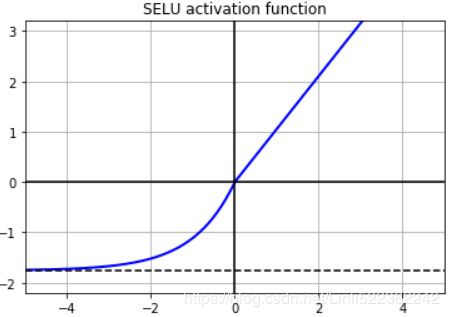

     By default, the SELU hyperparameters (scale and alpha) are tuned in such a way that the mean output of each neuron remains close to 0, and the standard deviation remains close to 1 (assuming the inputs are standardized with mean 0 and standard deviation 1 too###np.random.normal( size=(500, 100) )###). Using this activation function, even a 1,000 layer deep neural network preserves roughly mean 0 and standard deviation 1 across all layers, avoiding the exploding/vanishing gradients problem: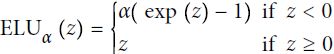

LeCun initialization is equivalent to Glorot initialization when .

np.random.seed(42)
#numpy.random.normal(loc=0.0, scale=1.0, size=None)¶
Z = np.random.normal( size=(500, 100) ) # standardized inputs
for layer in range(1000):
    W = np.random.normal( size=(100,100), scale=np.sqrt(1/100) ) #LeCun initialization #update weights
    Z = selu(np.dot(Z,W)) #np.dot(Z,W).shape=(500,100) ############
    means = np.mean(Z, axis=0).mean()
    stds = np.std(Z, axis=0).mean()
    if layer % 100 ==0:
        print("Layer {}: mean {:.2f}, std deviation {:.2f}".format(layer, means, stds))

Using SELU is easy:

keras.layers.Dense( 10, activation="selu", kernel_initializer="lecun_normal")

Let's create a neural net for Fashion MNIST with 100 hidden layers, using the SELU activation function:

np.random.seed(42)
tf.random.set_seed(42)

model = keras.models.Sequential()
model.add( keras.layers.Flatten(input_shape=[28,28]) )
#A Dense layer usually has weights of shape [number of inputs, number of neurons]
model.add( keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"))
#shape: inputs(instances, 784 features) dot W(784 features,300 neurons) = (instances,300 neurons)

for layer in range(99):
    model.add(keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"))
    
model.add( keras.layers.Dense(10, activation="softmax") )

model.compile( loss="sparse_categorical_crossentropy", \
              optimizer=keras.optimizers.SGD(lr=1e-3), \
              metrics=['accuracy'])

pixel_means = X_train.mean(axis=0, keepdims=True) # axis=0 for all instances # pixel_means.shape : (1, 28, 28)
pixel_stds = X_train.std(axis=0, keepdims=True) # pixel_stds.shape : (1, 28, 28)
X_train_scaled = (X_train-pixel_means)/pixel_stds
X_valid_scaled = (X_valid-pixel_means)/pixel_stds
X_test_scaled = (X_test - pixel_means)/pixel_stds

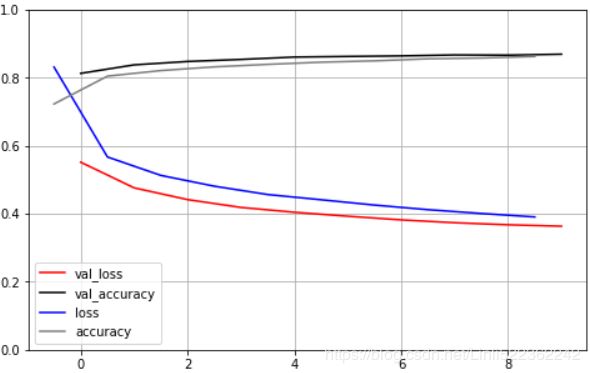
history = model.fit(X_train_scaled, y_train, epochs=5, validation_data=(X_valid_scaled, y_valid))

 

import pandas as pd
import matplotlib.pyplot as plt
 
colors=[#"blue", "gray", #  loss      accuracy
        "red", "black"] #   val_loss  val_accuracy
                               #df[ ["val_loss","val_accuracy"] ].plot(figsize=(8,5), color=colors)
pd.DataFrame( history.history )[["val_loss","val_accuracy"]].plot(figsize=(8,5), color=colors)

# the validation error is computed at the end of each epoch, while the training error is 
# computed using a running mean during each epoch. So the training curve should be shifted by 
# half an epoch to the left.
#shift(-0.5)
         #1D array                #list
plt.plot(np.arange(-0.5,4,1), history.history["loss"], c="blue", label="loss")    #must be put after previous code for plotting Dataframe
plt.plot(np.arange(-0.5,4,1), history.history["accuracy"], c="gray", label="accuracy")#must be put after previous code for plotting Dataframe
plt.legend()
plt.grid(True)
plt.gca().set_ylim(0,1) # set the vertical range to [0-1]
plt.show()

model.evaluate( X_test_scaled, y_test )

history.history['val_accuracy'][-1]

X_new = X_test[:3]

y_pred = model.predict_classes(X_new)
y_pred

  

y_test[:3]

Now look at what happens if we try to use the ReLU activation function instead:

np.random.seed(42)
tf.random.set_seed(42)

model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu", kernel_initializer="he_normal"))
for layer in range(99):
    model.add(keras.layers.Dense(100, activation="relu", kernel_initializer="he_normal"))
model.add(keras.layers.Dense(10, activation="softmax"))

model.compile( loss="sparse_categorical_crossentropy",
               optimizer=keras.optimizers.SGD(lr=1e-3),
               metrics=['accuracy']
             )

history = model.fit( X_train_scaled, y_train, epochs=5, validation_data=(X_valid_scaled, y_valid))

Not great at all, we suffered from the vanishing/exploding gradients problem().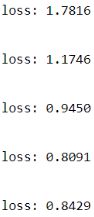

Proved: Although using He initialization along with ELU (or any variant of ReLU) can significantly reduce the danger of the vanishing/exploding gradients problems at the beginning of training, it doesn’t guarantee that they won’t come back during training.

model.evaluate( X_test_scaled, y_test )

history.history['val_accuracy'][-1]

X_new = X_test[:3]

y_pred = model.predict_classes(X_new)
y_pred

y_test[:3]

Batch Normalization

     Although using He initialization along with ELU (or any variant of ReLU) can significantly reduce the danger of the vanishing/exploding gradients problems at the beginning of training, it doesn’t guarantee that they won’t come back during training.

     In a 2015 paper, Sergey Ioffe and Christian Szegedy proposed a technique called Batch Normalization (BN) that addresses (solves) these problems. The technique consists of adding an operation in the model just before or after the activation function of each hidden layer. This operation simply zero-centers and normalizes each input, then scales and shifts the result using two new parameter vectors per layer: one for scaling, the other for shifting. In other words, the operation lets the model learn the optimal scale and mean of each of the layer’s inputs. In many cases, if you add a BN layer as the very first layer of your neural network, you do not need to standardize your training set (e.g., using a StandardScaler); the BN layer will do it for you (well, approximately, since it only looks at one batch at a time, and it can also rescale and shift each input feature).

从图像分析可知，数据经过标准化后，其形状保持大致不变，但尺寸被我们压缩至（-1, 1）之间，而原尺寸在(-80，80)之间。

　　通过平移和缩放，BN可以使数据被限定在我们想要的范围内，所以每层的输出数据都进行BN的话，可以使后层网络面对稳定的输入值，降低梯度发散的可能，从而加快训练速度；同时也意味着允许使用大点的学习率，加快收敛过程。

　　被缩放的数据让使用sigmoid或tanh激活函数在深层网络变成可能，并且在实际应用中β和γ是可以学习的，下图是一个直观的解释图。

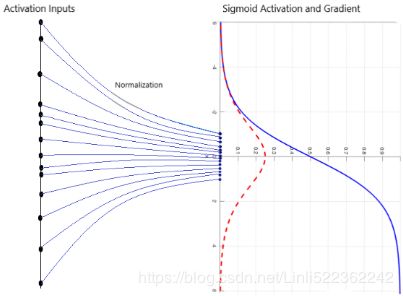
Batch Normalization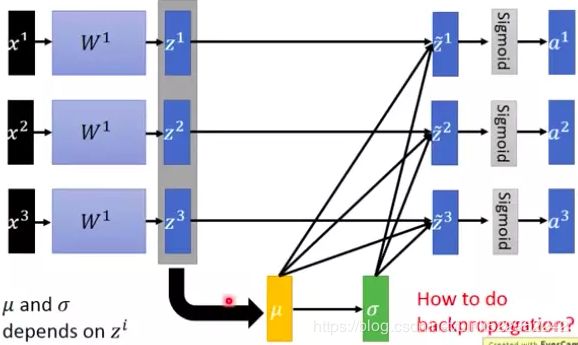

就是在前一层的线性输出 z 上做 normalization：需要求出这一 batch 数据的平均值和标准差,以及scale和offset，然后再经过激活函数，进入到下一层。

     In order to zero-center and normalize the inputs, the algorithm needs to estimate each input’s mean and standard deviation. It does so by evaluating the mean and standard deviation of the input over the current mini-batch (hence the name “Batch Normalization”). The whole operation is summarized step by step in Equation 11-3.

Equation 11-3. Batch Normalization algorithm

In this algorithm:

• is the vector of input means, evaluated over the whole mini-batch B (it contains one mean per input).
• is the vector of input standard deviations, also evaluated over the whole minibatch B(it contains one standard deviation per input).
• is the number of instances in the mini-batch.
• is the vector of zero-centered and normalized inputs for instance i.
• ε is a tiny number that avoids division by zero (typically ). This is called a smoothing term.
• γ is the output scale parameter vector for the layer (it contains one scale parameter per input feature).
• ⊗ represents element-wise multiplication逐元素乘法 (each input is multiplied by its corresponding output scale parameter γ).
• β is the output shift (offset) parameter vector for the layer (it contains one offset parameter per input). Each input is offset by its corresponding shift parameter.
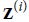• is the output of the BN(Batch Normalization) operation. It is a rescaled and shifted version of the inputs.

     So during training, BN standardizes its inputs, then rescales and offsets them. Good! What about at test time? Well, it’s not that simple. Indeed, we may need to make predictions for individual instances rather than for batches of instances: in this case, we will have no way to compute each input’s mean and standard deviation. Moreover, even if we do have a batch of instances, it may be too small, or the instances may not be independent and identically distributed, so computing statistics over the batch
instances would be unreliable. One solution could be to wait until the end of training, then run the whole training set through the neural network and compute the mean and standard deviation of each input of the BN layer. These “final” input means and standard deviations could then be used instead of the batch input means and standard deviations when making predictions. However, most implementations of Batch Normalization estimate these final statistics during training by using a moving average of the layer’s input means and standard deviations. This is what Keras does automatically when you use the BatchNormalization layer. To sum up, four parameter vectors are learned in each batch-normalized layer: γ (the output scale vector) and β (the output offset vector) are learned through regular backpropagation, and μ (the final input mean vector) and σ (the final input standard deviation vector) are estimated using an exponential moving average. Note that μ and σ are estimated during training, but they are used only after training (to replace the batch input means and standard deviations in Equation 11-3).

     Ioffe and Szegedy demonstrated that Batch Normalization considerably improved all the deep neural networks they experimented with, leading to a huge improvement in the ImageNet classification task (ImageNet is a large database of images classified into many classes, commonly used to evaluate computer vision systems). The vanishing gradients problem was strongly reduced, to the point that they could use saturating activation functions such as the tanh and even the logistic activation function. The networks were also much less sensitive to the weight initialization. The authors were able to use much larger learning rates, significantly speeding up the learning process. Specifically, they note that:

• Applied to a state-of-the-art最先进的 image classification model, Batch Normalization achieves the same accuracy with 14 times fewer training steps, and beats the original model by a significant margin. […] Using an ensemble of batch-normalized networks, we improve upon the best published result on ImageNet classification: reaching 4.9% top-5 validation error (and 4.8% test error), exceeding the accuracy of human raters.

Finally, like a gift that keeps on giving, Batch Normalization acts like a regularizer, reducing the need for other regularization techniques (such as dropout, described later in this chapter ).

     Batch Normalization does, however, add some complexity to the model (although it can remove the need for normalizing the input data, as we discussed earlier ###if you add a BN layer as the very first layer of your neural network, you do not need to standardize your training set (e.g., using a StandardScaler); the BN layer will do it for you (well, approximately, since it only looks at one batch at a time, and it can also rescale and shift each input feature).###). Moreover, there is a runtime penalty: the neural network makes slower predictions due to the extra computations required at each layer. Fortunately, it’s often possible to fuse融合 the BN layer with the previous layer, after training, thereby avoiding the runtime penalty. This is done by updating the previous layer’s weights and biases so that it directly produces outputs of the appropriate scale and offset. For example, if the previous layer computes XW + b, then the BN layer will compute
γ⊗(XW + b – μ)/σ + β (ignoring the smoothing term ε in the denominator). If we define W′ = γ⊗W/σ and b′ = γ⊗(b – μ)/σ + β, the equation simplifies to XW′ + b′. So if we replace the previous layer’s weights and biases (W and b) with the updated weights and biases (W′ and b′), we can get rid of the BN layer (TFLite’s optimizer does this automatically; see Chapter 19).

     You may find that training is rather slow, because each epoch takes much more time when you use Batch Normalization. This is usually counterbalanced平衡的 by the fact that convergence is much faster with BN, so it will take fewer epochs to reach the same performance. All in all, wall time will usually be shorter (this is the time measured by the clock on your wall).

Implementing Batch Normalization with Keras

     As with most things with Keras, implementing Batch Normalization is simple and intuitive. Just add a BatchNormalization layer before or after each hidden layer’s activation function, and optionally add a BN layer as well as the first layer in your
model.
For example, this model applies BN after every hidden layer and as the first layer in the model (after flattening the input images):

from tensorflow import keras

model = keras.models.Sequential([
    keras.layers.Flatten( input_shape=[28,28]),
    keras.layers.BatchNormalization(), #as the first layer in the model (after flattening the input images):

    keras.layers.Dense(300, activation="relu"),
    keras.layers.BatchNormalization(), #this model applies BN after every hidden layer

    keras.layers.Dense(100, activation="relu"),
    keras.layers.BatchNormalization(),

    keras.layers.Dense(10, activation="softmax")
])

    That’s all! In this tiny example with just two hidden layers, it’s unlikely that Batch Normalization will have a very positive impact; but for deeper networks it can make a tremendous difference.

Let’s display the model summary:

model.summary()

     As you can see, each BN layer adds four parameters per input: γ, β, μ, and σ (for example, the first BN layer adds 3,136 parameters, which is 4 × 784). The last two parameters, μ and σ, are the moving averages; they are not affected by backpropagation, so Keras calls them “non-trainable” (if you count the total number of BN parameters, 3,136 + 1,200 + 400, and divide by 2, you get 2,368, which is the total number of non-trainable parameters in this model).

model.layers

     Let’s look at the parameters of the first BN layer. Two are trainable (by backpropagation), and two are not:

bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]

     Now when you create a BN layer in Keras, it also creates two operations that will be called by Keras at each iteration during training. These operations will update the moving averages. Since we are using the TensorFlow backend, these operations are TensorFlow operations (we will discuss TF operations in Chapter 12):

model.layers[1].updates

(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
 
# scale the pixel intensities down to the 0–1 range by dividing them by 255.0 
#(this also converts them to floats)
X_train_full = X_train_full/255.0
X_test = X_test/255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]

model.compile( loss="sparse_categorical_crossentropy", 
               optimizer=keras.optimizers.SGD(lr=1e-3),
               metrics=["accuracy"]
             )

history = model.fit( X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))

import pandas as pd
import matplotlib.pyplot as plt
 
colors=[#"blue", "gray", #  loss      accuracy
        "red", "black"] #   val_loss  val_accuracy
                               #df[ ["val_loss","val_accuracy"] ].plot(figsize=(8,5), color=colors)
pd.DataFrame( history.history )[["val_loss","val_accuracy"]].plot(figsize=(8,5), color=colors)

# the validation error is computed at the end of each epoch, while the training error is 
# computed using a running mean during each epoch. So the training curve should be shifted by 
# half an epoch to the left.
#shift(-0.5)
         #1D array                #list
plt.plot(np.arange(-0.5,9,1), history.history["loss"], c="blue", label="loss")    #must be put after previous code for plotting Dataframe
plt.plot(np.arange(-0.5,9,1), history.history["accuracy"], c="gray", label="accuracy")#must be put after previous code for plotting Dataframe
plt.legend()
plt.grid(True)
plt.gca().set_ylim(0,1) # set the vertical range to [0-1]
plt.show()

 

​results = model.evaluate(X_test, y_test)

history.history['val_accuracy'][-1]

X_new = X_test[:3]

y_pred = model.predict_classes(X_new)
y_pred

###########################
most implementations of Batch Normalization estimate these final statistics during training by using a moving average of the layer’s input means and standard deviations. This is what Keras does automatically when you use the BatchNormalization layer.

So you don't need to retrain the model

np.random.seed(42)
tf.random.set_seed(42)

model = keras.models.Sequential([
    keras.layers.Flatten( input_shape=[28,28]),
    keras.layers.BatchNormalization(),

    keras.layers.Dense(300, activation="relu"),
    keras.layers.BatchNormalization(),

    keras.layers.Dense(100, activation="relu"),
    keras.layers.BatchNormalization(),

    keras.layers.Dense(10, activation="softmax")
])

model.compile( loss="sparse_categorical_crossentropy", 
               optimizer=keras.optimizers.SGD(lr=1e-3),
               metrics=["accuracy"]
             )

#If unspecified, `batch_size` will default to 32
history = model.fit( X_train_full, y_train_full, epochs=10)

model_ba.evaluate(X_test, y_test)

 

###########################

     The authors of the BN paper argued in favor of adding the BN layers before the activation functions, rather than after (as we just did). There is some debate about this, as which is preferable seems to depend on the task—you can experiment with this too to see which option works best on your dataset.

• you must remove the activation function from the hidden layers. Moreover, since a Batch Normalization layer includes one offset parameter per input, you can remove the bias term from the previous layer###the hidden layer### (just pass use_bias=False when creating it)
   
• To add the BN layers before the activation functions,
• add the activation functions as separate layers after the BN layers.

model_ba = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28,28]),    
    keras.layers.BatchNormalization(), 
   
    keras.layers.Dense(300, use_bias=False),
    keras.layers.BatchNormalization(),# To add BN layers before the activation
    # To use the reLU activation function, create a reLU layer and add it to your
    # model just after the layer you want to apply it to:
    keras.layers.Activation("relu"),
  
    keras.layers.Dense(100, use_bias=False),
    keras.layers.BatchNormalization(),
    keras.layers.Activation("relu"),
    
    keras.layers.Dense(10, activation="softmax")
])

model_ba.compile(loss="sparse_categorical_crossentropy", 
                 optimizer=keras.optimizers.SGD(lr=1e-3),
                 metrics=['accuracy'])
history_ba = model_ba.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))

     The BatchNormalization class has quite a few hyperparameters you can tweak. The defaults will usually be fine, but you may occasionally need to tweak the momentum动力,要素. This hyperparameter is used by the BatchNormalization layer when it updates the exponential moving averages; given a new value v (i.e., a new vector of input means or standard deviations computed over the current batch), the layer updates the running average using the following equation:
 <-- × momentum + v × (1 − momentum )

     A good momentum value is typically close to 1; for example, 0.9, 0.99, or 0.999 (you want more 9s for larger datasets and smaller mini-batches).

     Another important hyperparameter is axis: it determines which axis should be normalized. It defaults to –1, meaning that by default it will normalize the last axis (using the means and standard deviations computed across the other axes).

• When the input batch is 2D (i.e., the batch shape is [batch size, features]), this means that each input feature will be normalized based on the mean and standard deviation computed across all the instances(OR all rows) in the batch. For example, the first BN layer in the previous code example will independently normalize (and rescale and shift) each of the 784 input features.  ### keras.layers.Flatten(input_shape=[28,28])--> 1D for each instance or one instance per row
   
• If we move the first BN layer before the Flatten layer, then the input batches will be 3D, with shape [batch size, height, width]; therefore, the BN layer will compute 28 means and 28 standard deviations (1 per column of pixels, computed across all instances in the batch and across all rows(OR all heights) in the column(OR width)), and it will normalize all pixels in a given column using the same mean and standard deviation. There will also be just 28 scale parameters and 28 shift parameters. If instead you still want to treat each of the 784 pixels independently, then you should set axis=[1, 2].

     Notice that the BN layer does not perform the same computation during training and after training: it uses batch statistics during training and the “final” statistics after training (i.e., the final values of the moving averages). Let’s take a peek at the source code of this class to see how this is handled:

class BatchNormalization(keras.layers.Layer):
    [...]
    def call(self, inputs, training=None):
        [...]

     The call() method is the one that performs the computations; as you can see, it has an extra training argument, which is set to None by default, but the fit() method sets to it to 1 during training. If you ever need to write a custom layer, and it must
behave differently during training and testing, add a training argument to the call() method and use this argument in the method to decide what to compute(we will discuss custom layers in Chapter 12).

     BatchNormalization has become one of the most-used layers in deep neural networks, to the point that it is often omitted in the diagrams, as it is assumed that BN is added after every layer. But a recent paper by Hongyi Zhang et al. may change this assumption: by using a novel fixed-update (fixup) weight initialization technique, the authors managed to train a very deep neural network (10,000 layers!) without BN, achieving state-of-the-art performance on complex image classification tasks. As this is bleeding-edge research前沿研究, however, you may want to wait for additional research to confirm this finding before you drop Batch Normalization.

Gradient Clipping梯度裁剪

     Another popular technique to mitigate使减轻the exploding gradients problem is to clip剪掉 the gradients during backpropagation so that they never exceed some threshold. This is called Gradient Clipping. This technique is most often used in recurrent neural networks, as Batch Normalization is tricky to use in RNNs, as we will see in Chapter 15. For other types of networks, BN is usually sufficient足够的.

     In Keras, implementing Gradient Clipping is just a matter of setting the clipvalue or clipnorm argument when creating an optimizer, like this:

optimizer = keras.optimizers.SGD(clipnorm=1.0)
model.compile(loss="mse", optimizer=optimizer)

optimizer = keras.optimizers.SGD(clipvalue=1.0)
model.compile(loss="mse", optimizer=optimizer)

     This optimizer will clip every component of the gradient vector to a value between –1.0 and 1.0. This means that all the partial derivatives of the loss (with regard to each and every trainable parameter) will be clipped between –1.0 and 1.0. The threshold is a hyperparameter you can tune. Note that it may change the orientation of the gradient vector. For instance, if the original gradient vector is [0.9, 100.0], it points mostly in the direction of the second axis; but once you clip it by value, you get [0.9, 1.0], which points roughly in the diagonal between the two axes. In practice, this approach works well. If you want to ensure that Gradient Clipping does not change the direction of the gradient vector, you should clip by norm by setting clipnorm instead of clipvalue. This will clip the whole gradient if its ℓ2 norm is greater than the threshold you picked. For example, if you set clipnorm=1.0, then the vector [0.9, 100.0] will be clipped to [0.00899964, 0.9999595], preserving its orientation but almost eliminating the first component. If you observe that the gradients explode during training (you can track the size of the gradients using TensorBoard), you may want to try both clipping by value and clipping by norm, with different thresholds, and see which option performs best on the validation set.

Reusing Pretrained Layers

     It is generally not a good idea to train a very large DNN from scratch: instead, you should always try to find an existing neural network that accomplishes a similar task to the one you are trying to tackle (we will discuss how to find them in Chapter 14), then reuse the lower layers of this network. This technique is called transfer learning迁移学习. It will not only speed up training considerably, but also require significantly less training data.

     Suppose you have access to a DNN that was trained to classify pictures into 100 different categories, including animals, plants, vehicles, and everyday objects. You now want to train a DNN to classify specific types of vehicles. These tasks are very similar, even partly overlapping, so you should try to reuse parts of the first network (see Figure 11-4).

Figure 11-4. Reusing pretrained layers

     If the input pictures of your new task don’t have the same size as the ones used in the original task, you will usually have to add a preprocessing step to resize them to the size expected by the original model. More generally, transfer learning will work best when the inputs have similar low-level features.

     The output layer of the original model should usually be replaced because it is most likely not useful at all for the new task, and it may not even have the right number of outputs for the new task.

     Similarly, the upper hidden layers of the original model are less likely to be as useful as the lower layers, since the high-level features that are most useful for the new task may differ significantly from the ones that were most useful for the original task. You want to find the right number of layers to reuse.

     Try freezing all the reused layers first (i.e., make their weights non-trainable so that Gradient Descent won’t modify them), then train your model and see how it performs. Then try unfreezing one or two of the top hidden layers to let backpropagation tweak them and see if performance improves. The more training data you have, the more layers you can unfreeze. It is also useful to reduce the learning rate when you unfreeze reused layers: this will avoid wrecking破坏 their fine-tuned weights.

     If you still cannot get good performance, and you have little training data, try dropping the top hidden layer(s) and freezing all the remaining hidden layers again. You can iterate until you find the right number of layers to reuse. If you have plenty of training data, you may try replacing the top hidden layers instead of dropping them, and even adding more hidden layers.

Transfer Learning with Keras

https://blog.csdn.net/Linli522362242/article/details/106982127