numpy基本使用方法示例
前些天学了些numpy的基本用法。这里用jupyter notebook又熟悉了一遍,使用的环境是python3+windows,代码上传到csdn资源啦:ABC of Numpy
关于numpy学习还是强烈建议常去官方https://docs.scipy.org/doc/numpy/reference/里查一查各种用法和toturial等。
下面是jupyter notebook代码导出的md文件。
三种数据结构list/array/numpy.array和三种方法求和for/sum/numpy.sum 之间的效率对比。
format()函数
通过{}格式化字符串,与%类似
list_setup = """
import numpy
data = [1] * {}
s = 0
""".format(100)
list_setup'\nimport numpy\ndata = [1] * 100\ns = 0\n'
common_for = """
for d in data:
s += d
print(s)
"""
common_for'\nfor d in data:\n s += d\n \nprint(s)\n'
timeit — 测量小代码片的执行时间
timeit.timeit(stmt=’pass’, setup=’pass’, timer=, number=1000000)¶
用给定的语句、setup代码和timer函数创建一个Timer实例,并运行其timeit()方法number次。
参见:http://python.usyiyi.cn/python_278/library/timeit.html
import timeit
timeit.timeit(common_for, list_setup, number = 5)100
200
300
400
500
7.722676537014195e-05
import timeit
common_for = """
for d in data:
s += d
"""
common_sum = """
sum(data)
"""
common_numpy_sum = """
numpy.sum(data)
"""
def timeit_list(n, loops):
list_setup = """
import numpy
data = [1] * {}
s = 0
""".format(n)
print('list:')
print(timeit.timeit(common_for, list_setup, number = loops))
print(timeit.timeit(common_sum, list_setup, number = loops))
print(timeit.timeit(common_numpy_sum, list_setup, number = loops))
def timeit_array(n, loops):
array_setup = """
import numpy
import array
data = array.array('L', [1] * {})
s = 0
""".format(n)
print('array:')
print(timeit.timeit(common_for, array_setup, number = loops))
print(timeit.timeit(common_sum, array_setup, number = loops))
print(timeit.timeit(common_numpy_sum, array_setup, number = loops))
def timeit_numpy(n, loops):
numpy_setup = """
import numpy
data = numpy.array([1] * {})
s = 0
""".format(n)
print('numpy:')
print(timeit.timeit(common_for, numpy_setup, number = loops))
print(timeit.timeit(common_sum, numpy_setup, number = loops))
print(timeit.timeit(common_numpy_sum, numpy_setup, number = loops))
if __name__ == '__main__':
timeit_list(50000, 500)
timeit_array(50000, 500)
timeit_numpy(50000, 500)list:
1.2216241770122451
0.19332248745286051
1.3766720554735912
array:
1.2323744841060034
0.32563668348166175
0.01575084682758643
numpy:
2.640422366407165
2.063364347773131
0.013614950760484135
NumPy的ndarray 创建ndarray
import numpy as np
print('使用list生成NumPy一维数组')
data = [6, 7.5, 8, 0, 1]
arr = np.array(data)
print(arr)
print('打印元素类型')
print(arr.dtype)
print()
print('使用list生成NumPy二维数组')
data = [[1, 2, 3, 4], [5, 6, 7, 8]]
arr = np.array(data)
print(arr)
print('打印数组维度')
print(arr.shape)
print()
print('使用zeros/empty')
print(np.zeros(10)) # 生成包含10个0的一维数组
print(np.zeros((3, 6))) # 生成3*6的二维数组
print()
print('使用arrange生成连续元素')
print(np.arange(15)) # [0, 1, 2, ..., 14]使用list生成NumPy一维数组
[ 6. 7.5 8. 0. 1. ]
打印元素类型
float64
使用list生成NumPy二维数组
[[1 2 3 4]
[5 6 7 8]]
打印数组维度
(2, 4)
使用zeros/empty
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[[ 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0.]]
使用arrange生成连续元素
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
NumPy的ndarray 创建ndarray 数组和标量之间的运算
import numpy as np
# 数组乘法/减法,对应元素相乘/相减。
arr = np.array([[1.0, 2.0, 3.0], [4., 5., 6.]])
print(arr * arr)
print(arr - arr)
print()
# 标量操作作用在数组的每个元素上
arr = np.array([[1.0, 2.0, 3.0], [4., 5., 6.]])
print(1 / arr)
print(arr ** 0.5) # 开根号[[ 1. 4. 9.]
[ 16. 25. 36.]]
[[ 0. 0. 0.]
[ 0. 0. 0.]]
[[ 1. 0.5 0.33333333]
[ 0.25 0.2 0.16666667]]
[[ 1. 1.41421356 1.73205081]
[ 2. 2.23606798 2.44948974]]
NumPy的ndarray 基本的索引和切片
使用整数索引时将降低一个维度,使用切片索引不降低维度
import numpy as np
# 通过索引访问二维数组某一行或某个元素
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(arr[2])
print(arr[0][2])
print(arr[0, 2]) # 普通Python数组不能用。
print()
# 对更高维数组的访问和操作
arr = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print(arr)
print(arr[0]) # 结果是个2维数组
print(arr[1, 0]) # 结果是个1维数组
old_values = arr[0].copy() # 复制arr[0]的值
arr[0] = 42 # 把arr[0]所有的元素都设置为同一个值
print(arr)
arr[0] = old_values # 把原来的数组写回去
print(arr)
print()
print('使用切片访问和操作数组')
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
print(arr[1:6]) # 打印元素arr[1]到arr[5]
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(arr[:2]) # 打印第1、2行
print(arr[:2, 1:]) # 打印第1、2行,第2、3列
print(arr[:, :1]) # 打印第一列的所有元素
arr[:2, 1:] = 0 # 第1、2行,第2、3列的元素设置为0
print(arr)[7 8 9]
3
3
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
[[1 2 3]
[4 5 6]]
[7 8 9]
[[[42 42 42]
[42 42 42]]
[[ 7 8 9]
[10 11 12]]]
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
使用切片访问和操作数组
[2 3 4 5 6]
[[1 2 3]
[4 5 6]]
[[2 3]
[5 6]]
[[1]
[4]
[7]]
[[1 0 0]
[4 0 0]
[7 8 9]]
NumPy的ndarray 布尔型索引
import numpy as np
import numpy.random as np_random
print('使用布尔数组作为索引')
name_arr = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
rnd_arr = np_random.randn(7, 4) # 随机7*4数组
print("rnd_arr:\n",rnd_arr)
print("name_arr == 'Bob':\n", name_arr == 'Bob') # 返回布尔数组,元素等于'Bob'为True,否则False。
print("rnd_arr[name_arr == 'Bob']:\n", rnd_arr[name_arr == 'Bob']) # 利用布尔数组选择行
print("rnd_arr[name_arr == 'Bob', :2]:\n", rnd_arr[name_arr == 'Bob', :2]) # 增加限制打印列的范围
print("rnd_arr[~(name_arr == 'Bob')]:\n", rnd_arr[-(name_arr == 'Bob')]) # 对布尔数组的内容取反
mask_arr = (name_arr == 'Bob') | (name_arr == 'Will') # 逻辑运算混合结果
print("rnd_arr[mask_arr]:\n",rnd_arr[mask_arr])
rnd_arr[name_arr != 'Joe'] = 7 # 先布尔数组选择行,然后把每行的元素设置为7。
print("rnd_arr:\n", rnd_arr)使用布尔数组作为索引
rnd_arr:
[[ 0.91195971 -1.72383144 -0.87595945 0.91695143]
[-1.0445351 0.52281564 0.18632544 0.89680185]
[-0.99298998 0.03255189 0.34324589 -0.38039068]
[ 0.42797948 -1.15371266 -0.21248912 -0.59456161]
[ 2.25764476 0.45040018 -1.03121475 1.16941102]
[-1.39247853 -0.74292563 -1.60210982 -0.27815867]
[-1.60465891 -0.39125059 -0.63173921 0.49464832]]
name_arr == 'Bob':
[ True False False True False False False]
rnd_arr[name_arr == 'Bob']:
[[ 0.91195971 -1.72383144 -0.87595945 0.91695143]
[ 0.42797948 -1.15371266 -0.21248912 -0.59456161]]
rnd_arr[name_arr == 'Bob', :2]:
[[ 0.91195971 -1.72383144]
[ 0.42797948 -1.15371266]]
rnd_arr[~(name_arr == 'Bob')]:
[[-1.0445351 0.52281564 0.18632544 0.89680185]
[-0.99298998 0.03255189 0.34324589 -0.38039068]
[ 2.25764476 0.45040018 -1.03121475 1.16941102]
[-1.39247853 -0.74292563 -1.60210982 -0.27815867]
[-1.60465891 -0.39125059 -0.63173921 0.49464832]]
rnd_arr[mask_arr]:
[[ 0.91195971 -1.72383144 -0.87595945 0.91695143]
[-0.99298998 0.03255189 0.34324589 -0.38039068]
[ 0.42797948 -1.15371266 -0.21248912 -0.59456161]
[ 2.25764476 0.45040018 -1.03121475 1.16941102]]
rnd_arr:
[[ 7. 7. 7. 7. ]
[-1.0445351 0.52281564 0.18632544 0.89680185]
[ 7. 7. 7. 7. ]
[ 7. 7. 7. 7. ]
[ 7. 7. 7. 7. ]
[-1.39247853 -0.74292563 -1.60210982 -0.27815867]
[-1.60465891 -0.39125059 -0.63173921 0.49464832]]
C:\Program Files\Anaconda3\lib\site-packages\ipykernel\__main__.py:11: DeprecationWarning: numpy boolean negative, the `-` operator, is deprecated, use the `~` operator or the logical_not function instead.
NumPy的ndarray 花式索引(Fancy indexing)
即利用整数数组进行索引,这种方式的索引将会构建一个新的数组,而切片的方法只是原数组的一个view
import numpy as np
print('Fancy Indexing: 使用整数数组作为索引')
arr = np.empty((8, 4))
for i in range(8):
arr[i] = i
print("arr:\n", arr)
print(arr[[4, 3, 0, 6]]) # 打印arr[4]、arr[3]、arr[0]和arr[6]。
print(arr[[-3, -5, -7]]) # 打印arr[-3]、arr[-5]和arr[-7]行
arr = np.arange(32).reshape((8, 4)) # 通过reshape变换成二维数组
print("arr:\n", arr)
print(arr[[1, 5, 7, 2], [0, 3, 1, 2]]) # 打印arr[1, 0]、arr[5, 3],arr[7, 1]和arr[2, 2]
print(arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]) # 1572行的0312列
print(arr[np.ix_([1, 5, 7, 2], [0, 3, 1, 2])]) # 可读性更好的写法Fancy Indexing: 使用整数数组作为索引
arr:
[[ 0. 0. 0. 0.]
[ 1. 1. 1. 1.]
[ 2. 2. 2. 2.]
[ 3. 3. 3. 3.]
[ 4. 4. 4. 4.]
[ 5. 5. 5. 5.]
[ 6. 6. 6. 6.]
[ 7. 7. 7. 7.]]
[[ 4. 4. 4. 4.]
[ 3. 3. 3. 3.]
[ 0. 0. 0. 0.]
[ 6. 6. 6. 6.]]
[[ 5. 5. 5. 5.]
[ 3. 3. 3. 3.]
[ 1. 1. 1. 1.]]
arr:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]
[24 25 26 27]
[28 29 30 31]]
[ 4 23 29 10]
[[ 4 7 5 6]
[20 23 21 22]
[28 31 29 30]
[ 8 11 9 10]]
[[ 4 7 5 6]
[20 23 21 22]
[28 31 29 30]
[ 8 11 9 10]]
NumPy的ndarray 数组转置和轴兑换
即利用整数数组进行索引,这种方式的索引将会构建一个新的数组,而切片的方法只是原数组的一个view
import numpy as np
import numpy.random as np_random
print('转置矩阵')
arr = np.arange(15).reshape((3, 5))
print(arr)
print(arr.T)
print()
print('转置矩阵做点积')
arr = np_random.randn(6, 3)
print(np.dot(arr.T, arr))
print()
print('高维矩阵转换')
arr = np.arange(16).reshape((2, 2, 4))
print(arr)
'''
详细解释:
arr数组的内容为
- a[0][0] = [0, 1, 2, 3]
- a[0][1] = [4, 5, 6, 7]
- a[1][0] = [8, 9, 10, 11]
- a[1][1] = [12, 13, 14, 15]
transpose的参数为坐标,正常顺序为(0, 1, 2, ... , n - 1),
现在传入的为(1, 0, 2)代表a[x][y][z] = a[y][x][z],第0个和第1个坐标互换。
- a'[0][0] = a[0][0] = [0, 1, 2, 3]
- a'[0][1] = a[1][0] = [8, 9, 10, 11]
- a'[1][0] = a[0][1] = [4, 5, 6, 7]
- a'[1][1] = a[1][1] = [12, 13, 14, 15]
'''
print(arr.transpose((1, 0, 2)))
print(arr.swapaxes(1, 2)) # 直接交换第1和第2个坐标转置矩阵
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
[[ 0 5 10]
[ 1 6 11]
[ 2 7 12]
[ 3 8 13]
[ 4 9 14]]
转置矩阵做点积
[[ 5.06870258 -3.64761969 -0.65129265]
[-3.64761969 5.89679079 1.4014983 ]
[-0.65129265 1.4014983 1.84146533]]
高维矩阵转换
[[[ 0 1 2 3]
[ 4 5 6 7]]
[[ 8 9 10 11]
[12 13 14 15]]]
[[[ 0 1 2 3]
[ 8 9 10 11]]
[[ 4 5 6 7]
[12 13 14 15]]]
[[[ 0 4]
[ 1 5]
[ 2 6]
[ 3 7]]
[[ 8 12]
[ 9 13]
[10 14]
[11 15]]]
NumPy的ndarray 快速的元素级数据函数
import numpy as np
import numpy.random as np_random
print('求平方根')
arr = np.arange(10)
print(np.sqrt(arr))
print()
print('数组比较')
x = np_random.randn(8)
y = np_random.randn(8)
print(x)
print(y)
print(np.maximum(x, y))
print()
print('使用modf函数把浮点数分解成整数和小数部分')
arr = np_random.randn(7) * 5 # 统一乘5
print(np.modf(arr))求平方根
[ 0. 1. 1.41421356 1.73205081 2. 2.23606798
2.44948974 2.64575131 2.82842712 3. ]
数组比较
[-0.2425273 0.49360459 -0.57346039 -1.64999403 0.82632642 -0.72292287
-1.01101699 -1.18614948]
[ 0.09882292 -0.425122 -1.37039201 0.65600735 -0.03037832 0.21868377
-2.33294022 0.56566999]
[ 0.09882292 0.49360459 -0.57346039 0.65600735 0.82632642 0.21868377
-1.01101699 0.56566999]
使用modf函数把浮点数分解成整数和小数部分
(array([ 0.58120027, 0.74499931, 0.33690089, 0.39179341, -0.74925164,
0.03612071, -0.18781612]), array([ 7., 5., 0., 5., -10., 1., -2.]))
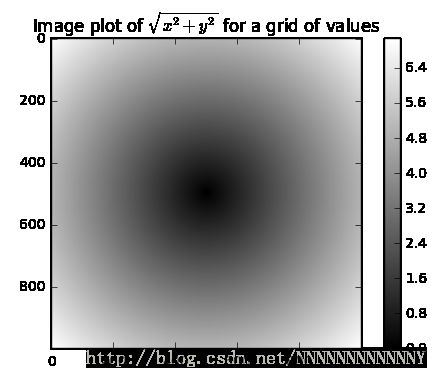
利用数组进行数据处理 简介
使用数组表达式代替循环的做法,通常被称为矢量化。
矢量化数组运算要比等价的纯python方式快上一两个数量级
import matplotlib.pyplot as plt
import numpy as np
import pylab
points = np.arange(-5, 5, 0.01) # 生成100个点
xs, ys = np.meshgrid(points, points) # xs, ys互为转置矩阵
print(xs)
print(ys)
z = np.sqrt(xs ** 2 + ys ** 2)
print(z)
# 画图
plt.imshow(z, cmap = plt.cm.gray);
plt.colorbar()
plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
pylab.show() [[-5. -4.99 -4.98 ..., 4.97 4.98 4.99]
[-5. -4.99 -4.98 ..., 4.97 4.98 4.99]
[-5. -4.99 -4.98 ..., 4.97 4.98 4.99]
...,
[-5. -4.99 -4.98 ..., 4.97 4.98 4.99]
[-5. -4.99 -4.98 ..., 4.97 4.98 4.99]
[-5. -4.99 -4.98 ..., 4.97 4.98 4.99]]
[[-5. -5. -5. ..., -5. -5. -5. ]
[-4.99 -4.99 -4.99 ..., -4.99 -4.99 -4.99]
[-4.98 -4.98 -4.98 ..., -4.98 -4.98 -4.98]
...,
[ 4.97 4.97 4.97 ..., 4.97 4.97 4.97]
[ 4.98 4.98 4.98 ..., 4.98 4.98 4.98]
[ 4.99 4.99 4.99 ..., 4.99 4.99 4.99]]
[[ 7.07106781 7.06400028 7.05693985 ..., 7.04988652 7.05693985
7.06400028]
[ 7.06400028 7.05692568 7.04985815 ..., 7.04279774 7.04985815
7.05692568]
[ 7.05693985 7.04985815 7.04278354 ..., 7.03571603 7.04278354
7.04985815]
...,
[ 7.04988652 7.04279774 7.03571603 ..., 7.0286414 7.03571603
7.04279774]
[ 7.05693985 7.04985815 7.04278354 ..., 7.03571603 7.04278354
7.04985815]
[ 7.06400028 7.05692568 7.04985815 ..., 7.04279774 7.04985815
7.05692568]]
利用数组进行数据处理 将条件逻辑表述为数组运算
numpy.where()函数
import numpy as np
import numpy.random as np_random
'''
关于zip函数的一点解释,zip可以接受任意多参数,然后重新组合成1个tuple列表。
zip([1, 2, 3], [4, 5, 6], [7, 8, 9])
返回结果:[(1, 4, 7), (2, 5, 8), (3, 6, 9)]
'''
print('通过真值表选择元素')
x_arr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
y_arr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])
result = [(x if c else y) for x, y, c in zip(x_arr, y_arr, cond)] # 通过列表推到实现
print(result)
print(np.where(cond, x_arr, y_arr)) # 使用NumPy的where函数
print()
print('更多where的例子')
arr = np_random.randn(4, 4)
print(arr)
print(np.where(arr > 0, 2, -2))
print(np.where(arr > 0, 2, arr))
print()
print('where嵌套')
cond_1 = np.array([True, False, True, True, False])
cond_2 = np.array([False, True, False, True, False])
# 传统代码如下
result = []
for i in range(len(cond)):
if cond_1[i] and cond_2[i]:
result.append(0)
elif cond_1[i]:
result.append(1)
elif cond_2[i]:
result.append(2)
else:
result.append(3)
print(result)
# np版本代码
result = np.where(cond_1 & cond_2, 0, \
np.where(cond_1, 1, np.where(cond_2, 2, 3)))
print(result)通过真值表选择元素
[1.1000000000000001, 2.2000000000000002, 1.3, 1.3999999999999999, 2.5]
[ 1.1 2.2 1.3 1.4 2.5]
更多where的例子
[[-1.70279977 -0.06533893 0.30055928 -0.20268285]
[-1.08928851 0.62551805 0.13070598 0.51931389]
[-0.33121132 -0.66843238 1.700761 1.11943521]
[ 0.90299866 -0.98016793 -0.27124416 0.73619528]]
[[-2 -2 2 -2]
[-2 2 2 2]
[-2 -2 2 2]
[ 2 -2 -2 2]]
[[-1.70279977 -0.06533893 2. -0.20268285]
[-1.08928851 2. 2. 2. ]
[-0.33121132 -0.66843238 2. 2. ]
[ 2. -0.98016793 -0.27124416 2. ]]
where嵌套
[1, 2, 1, 0, 3]
[1 2 1 0 3]
利用数组进行数据处理 数学和统计方法
import numpy as np
import numpy.random as np_random
print('求和,求平均')
arr = np.random.randn(5, 4)
print(arr)
print(arr.mean())
print(arr.sum())
print(arr.mean(axis = 1)) # 对每一行的元素求平均
print(arr.sum(0)) # 对每一列元素求和,axis可以省略。
print()
'''
cumsum:
- 按列操作:a[i][j] += a[i - 1][j]
- 按行操作:a[i][j] *= a[i][j - 1]
cumprod:
- 按列操作:a[i][j] += a[i - 1][j]
- 按行操作:a[i][j] *= a[i][j - 1]
'''
print('cunsum和cumprod函数演示')
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
print(arr)
print(arr.cumsum(0))
print(arr.cumprod(1))求和,求平均
[[-1.61670959 0.19908935 0.27933197 0.79743033]
[-0.39815355 0.07085717 0.77060031 -1.22171512]
[ 1.31918487 -0.27046673 -0.4804778 -0.22358837]
[ 0.09286317 0.25406849 -0.54765491 -0.60580501]
[ 0.07228479 1.729656 -0.45541003 -0.75120897]]
-0.0492911819757
-0.985823639514
[-0.08521448 -0.1946028 0.08616299 -0.20163207 0.14883045]
[-0.53053031 1.98320427 -0.43361046 -2.00488715]
cunsum和cumprod函数演示
[[0 1 2]
[3 4 5]
[6 7 8]]
[[ 0 1 2]
[ 3 5 7]
[ 9 12 15]]
[[ 0 0 0]
[ 3 12 60]
[ 6 42 336]]
利用数组进行数据处理 用于布尔型数组的方法
import numpy as np
import numpy.random as np_random
print('对正数求和')
arr = np_random.randn(100)
print((arr > 0).sum())
print()
print('对数组逻辑操作')
bools = np.array([False, False, True, False])
print(bools.any()) # 有一个为True则返回True
print(bools.all()) # 有一个为False则返回False对正数求和
52
对数组逻辑操作
True
False
利用数组进行数据处理 排序
import numpy as np
import numpy.random as np_random
print('一维数组排序')
arr = np_random.randn(8)
arr.sort()
print(arr)
print()
print('二维数组排序')
arr = np_random.randn(5, 3)
print(arr)
arr.sort(1) # 对每一行元素做排序
print(arr)
print('找位置在5%的数字')
large_arr = np_random.randn(1000)
large_arr.sort()
print(large_arr[int(0.05 * len(large_arr))])一维数组排序
[-1.2254574 -0.97713903 -0.88963314 -0.37754719 -0.26796988 0.15555375
0.52308261 0.62992375]
二维数组排序
[[ 0.24225847 -0.82665001 0.58079956]
[ 0.19780714 -1.36320096 -0.19915331]
[ 1.37567141 0.4404058 0.6511375 ]
[ 0.01552011 0.0888497 0.98564928]
[-1.16565493 -1.45890948 -0.16067809]]
[[-0.82665001 0.24225847 0.58079956]
[-1.36320096 -0.19915331 0.19780714]
[ 0.4404058 0.6511375 1.37567141]
[ 0.01552011 0.0888497 0.98564928]
[-1.45890948 -1.16565493 -0.16067809]]
找位置在5%的数字
-1.54860617706
利用数组进行数据处理 去重以及其他集合运算
import numpy as np
import numpy.random as np_random
print('用unique函数去重')
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
print(sorted(set(names))) # 传统Python做法
print(np.unique(names))
ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
print(np.unique(ints))
print()
print('查找数组元素是否在另一数组')
values = np.array([6, 0, 0, 3, 2, 5, 6])
print(np.in1d(values, [2, 3, 6]))用unique函数去重
['Bob', 'Joe', 'Will']
['Bob' 'Joe' 'Will']
[1 2 3 4]
查找数组元素是否在另一数组
[ True False False True True False True]
数组文件的输入输出
import numpy as np
print('数组文件读写')
arr = np.arange(10)
np.save('some_array', arr)
print(np.load('some_array.npy'))
print()
print('多个数组压缩存储')
np.savez('array_archive.npz', a = arr, b = arr)
arch = np.load('array_archive.npz')
print(arch['b'])数组文件读写
[0 1 2 3 4 5 6 7 8 9]
多个数组压缩存储
[0 1 2 3 4 5 6 7 8 9]
import numpy as np
print('读取csv文件做为数组')
arr = np.loadtxt('array_ex.txt', delimiter = ',')
print(arr)读取csv文件做为数组
[[ 0.580052 0.18673 1.040717 1.134411]
[ 0.194163 -0.636917 -0.938659 0.124094]
[-0.12641 0.268607 -0.695724 0.047428]
[-1.484413 0.004176 -0.744203 0.005487]
[ 2.302869 0.200131 1.670238 -1.88109 ]
[-0.19323 1.047233 0.482803 0.960334]]
线性代数
import numpy as np
import numpy.random as np_random
from numpy.linalg import inv, qr
print('矩阵乘法')
x = np.array([[1., 2., 3.], [4., 5., 6.]])
y = np.array([[6., 23.], [-1, 7], [8, 9]])
print(x.dot(y))
print(np.dot(x, np.ones(3)))
x = np_random.randn(5, 5)
print()
print('矩阵求逆')
mat = x.T.dot(x)
print(inv(mat)) # 矩阵求逆
print(mat.dot(inv(mat))) # 与逆矩阵相乘,得到单位矩阵。
print()
print('矩阵消元')
print(mat)
q, r = qr(mat)
print(q)
print(r)矩阵乘法
[[ 28. 64.]
[ 67. 181.]]
[ 6. 15.]
矩阵求逆
[[ 1.98707396 -0.53288822 -0.46170685 1.40851133 0.98034855]
[-0.53288822 0.32498877 0.1739078 -0.49283094 -0.32322116]
[-0.46170685 0.1739078 0.28718445 -0.44293138 -0.28555373]
[ 1.40851133 -0.49283094 -0.44293138 1.70245336 0.86902909]
[ 0.98034855 -0.32322116 -0.28555373 0.86902909 0.68740921]]
[[ 1.00000000e+00 5.81365320e-17 -1.26510863e-17 -2.78216399e-17
2.63778304e-17]
[ -1.24388415e-15 1.00000000e+00 3.27664224e-16 -6.10102428e-16
-1.00945346e-16]
[ -3.97928099e-16 2.09300548e-16 1.00000000e+00 -1.86132725e-16
-1.87884457e-16]
[ -1.62514319e-16 1.43641883e-16 -5.96301772e-17 1.00000000e+00
5.83954300e-17]
[ -1.02069500e-15 4.45197485e-16 2.26357372e-16 -7.57375375e-16
1.00000000e+00]]
矩阵消元
[[ 1.90987653 0.52193904 0.28873755 -0.42303606 -1.82360404]
[ 0.52193904 6.54430414 -1.06822345 0.62154789 1.10326864]
[ 0.28873755 -1.06822345 6.60057114 0.66576341 0.98618705]
[-0.42303606 0.62154789 0.66576341 1.951651 -1.29516746]
[-1.82360404 1.10326864 0.98618705 -1.29516746 6.62125971]]
[[-0.69702087 -0.00840117 -0.05347 0.32640194 0.63615569]
[-0.19048478 -0.95239436 -0.10530405 -0.03975455 -0.20974069]
[-0.1053765 0.16898045 -0.96213928 -0.01714816 -0.185298 ]
[ 0.15438954 -0.10754374 -0.13025985 -0.79348928 0.56391963]
[ 0.66553521 -0.22968314 -0.2082604 0.51182229 0.44606511]]
[[-2.74005644 -0.66760244 0.06580827 -0.45435131 5.16373443]
[ 0. -6.73789796 1.83220255 -0.38831342 -2.25028468]
[ 0. 0. -6.54572525 -0.66787858 -2.17775774]
[ 0. 0. 0. -2.38571548 3.76061069]
[ 0. 0. 0. 0. 0.64890767]]
随机数生成
import numpy as np
import numpy.random as np_random
from random import normalvariate
print('正态分布随机数')
samples = np.random.normal(size=(4, 4))
print(samples)
print('批量按正态分布生成0到1的随机数')
N = 10
print([normalvariate(0, 1) for _ in range(N)])
print(np.random.normal(size = N)) # 与上面代码等价正态分布随机数
[[ 0.34626452 -0.64319197 0.20531044 0.50882782]
[-0.50942437 -0.96321658 0.37254189 -2.22577193]
[-0.94374973 0.63903227 0.3812968 -0.21730856]
[ 0.82269253 0.6827586 1.31978117 -0.72241684]]
批量按正态分布生成0到1的随机数
[0.9126704020025768, 0.8500947334336287, -0.022045070030965477, 0.9787424604478941, 1.2797147008376195, -0.4655910363624607, 1.0251260380221932, 1.08897118803527, 0.3830111268649084, -0.18690464553744496]
[-0.40017888 -0.57229308 0.41729841 1.83018917 -0.17923887 -1.47785736
-0.83107611 -1.02309879 -1.36712807 0.08832523]
高级应用 数组重塑
import numpy as np
print("将一维数组转换为二维数组")
arr = np.arange(8)
print(arr.reshape((4, 2)))
print(arr.reshape((4, 2)).reshape((2, 4))) # 支持链式操作
print()
print("维度大小自动推导")
arr = np.arange(15)
print(arr.reshape((5, -1)))
print()
print("获取维度信息并应用")
other_arr = np.ones((3, 5))
print(other_arr.shape)
print(arr.reshape(other_arr.shape))
print()
print("高维数组拉平")
arr = np.arange(15).reshape((5, 3))
print(arr.ravel())将一维数组转换为二维数组
[[0 1]
[2 3]
[4 5]
[6 7]]
[[0 1 2 3]
[4 5 6 7]]
维度大小自动推导
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]]
获取维度信息并应用
(3, 5)
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
高维数组拉平
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
高级应用 数组的合并与拆分
import numpy as np
import numpy.random as np_random
print('连接两个二维数组')
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([[7, 8, 9], [10, 11, 12]])
print(np.concatenate([arr1, arr2], axis = 0)) # 按行连接
print(np.concatenate([arr1, arr2], axis = 1)) # 按列连接
print()
# 所谓堆叠,参考叠盘子。。。连接的另一种表述
print('垂直stack与水平stack')
print(np.vstack((arr1, arr2))) # 垂直堆叠
print(np.hstack((arr1, arr2))) # 水平堆叠
print()
print('拆分数组')
arr = np_random.randn(5, 5)
print(arr)
print('水平拆分')
first, second, third = np.split(arr, [1, 3], axis = 0)
print('first')
print(first)
print('second')
print(second)
print('third')
print(third)
print('垂直拆分')
first, second, third = np.split(arr, [1, 3], axis = 1)
print('first')
print(first)
print('second')
print(second)
print('third')
print(third)
print()
# 堆叠辅助类
arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np_random.randn(3, 2)
print('r_用于按行堆叠')
print(np.r_[arr1, arr2])
print('c_用于按列堆叠')
print(np.c_[np.r_[arr1, arr2], arr])
print('切片直接转为数组')
print(np.c_[1:6, -10:-5])连接两个二维数组
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
[[ 1 2 3 7 8 9]
[ 4 5 6 10 11 12]]
垂直stack与水平stack
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
[[ 1 2 3 7 8 9]
[ 4 5 6 10 11 12]]
拆分数组
[[ 0.96959321 1.22709255 0.433002 1.24900503 0.13181234]
[ 1.678499 -0.87083568 0.88049665 1.45094783 0.60742806]
[-0.2840544 -1.18128281 -0.75718389 -1.58781811 1.13913897]
[ 1.1393683 -1.42725118 0.07802397 -0.32087879 -0.01869892]
[ 0.15856496 0.37080343 -0.78025804 -0.05116768 -1.53760895]]
水平拆分
first
[[ 0.96959321 1.22709255 0.433002 1.24900503 0.13181234]]
second
[[ 1.678499 -0.87083568 0.88049665 1.45094783 0.60742806]
[-0.2840544 -1.18128281 -0.75718389 -1.58781811 1.13913897]]
third
[[ 1.1393683 -1.42725118 0.07802397 -0.32087879 -0.01869892]
[ 0.15856496 0.37080343 -0.78025804 -0.05116768 -1.53760895]]
垂直拆分
first
[[ 0.96959321]
[ 1.678499 ]
[-0.2840544 ]
[ 1.1393683 ]
[ 0.15856496]]
second
[[ 1.22709255 0.433002 ]
[-0.87083568 0.88049665]
[-1.18128281 -0.75718389]
[-1.42725118 0.07802397]
[ 0.37080343 -0.78025804]]
third
[[ 1.24900503 0.13181234]
[ 1.45094783 0.60742806]
[-1.58781811 1.13913897]
[-0.32087879 -0.01869892]
[-0.05116768 -1.53760895]]
r_用于按行堆叠
[[ 0. 1. ]
[ 2. 3. ]
[ 4. 5. ]
[ 1.33109552 -0.0830555 ]
[ 0.19346402 1.72261669]
[-1.11629341 -0.56054053]]
c_用于按列堆叠
[[ 0. 1. 0. ]
[ 2. 3. 1. ]
[ 4. 5. 2. ]
[ 1.33109552 -0.0830555 3. ]
[ 0.19346402 1.72261669 4. ]
[-1.11629341 -0.56054053 5. ]]
切片直接转为数组
[[ 1 -10]
[ 2 -9]
[ 3 -8]
[ 4 -7]
[ 5 -6]]
高级应用 元素的重复操作
import numpy as np
import numpy.random as np_random
print('Repeat: 按元素')
arr = np.arange(3)
print(arr.repeat(3))
print(arr.repeat([2, 3, 4])) # 3个元素,分别复制2, 3, 4次。长度要匹配!
print()
print('Repeat,指定轴')
arr = np_random.randn(2, 2)
print(arr)
print(arr.repeat(2, axis = 0)) # 按行repeat
print(arr.repeat(2, axis = 1)) # 按列repeat
print()
print('Tile: 参考贴瓷砖')
print(np.tile(arr, 2))
print(np.tile(arr, (2, 3))) # 指定每个轴的tile次数
Repeat: 按元素
[0 0 0 1 1 1 2 2 2]
[0 0 1 1 1 2 2 2 2]
Repeat,指定轴
[[-1.24977283 0.6218948 ]
[-0.6769229 -0.10062309]]
[[-1.24977283 0.6218948 ]
[-1.24977283 0.6218948 ]
[-0.6769229 -0.10062309]
[-0.6769229 -0.10062309]]
[[-1.24977283 -1.24977283 0.6218948 0.6218948 ]
[-0.6769229 -0.6769229 -0.10062309 -0.10062309]]
Tile: 参考贴瓷砖
[[-1.24977283 0.6218948 -1.24977283 0.6218948 ]
[-0.6769229 -0.10062309 -0.6769229 -0.10062309]]
[[-1.24977283 0.6218948 -1.24977283 0.6218948 -1.24977283 0.6218948 ]
[-0.6769229 -0.10062309 -0.6769229 -0.10062309 -0.6769229 -0.10062309]
[-1.24977283 0.6218948 -1.24977283 0.6218948 -1.24977283 0.6218948 ]
[-0.6769229 -0.10062309 -0.6769229 -0.10062309 -0.6769229 -0.10062309]]
高级应用 花式索引的等价函数
import numpy as np
import numpy.random as np_random
print('Fancy Indexing例子代码')
arr = np.arange(10) * 100
inds = [7, 1, 2, 6]
print(arr[inds])
print()
print('使用take')
print(arr.take(inds))
print()
print('使用put更新内容')
arr.put(inds, 50)
print(arr)
arr.put(inds, [70, 10, 20, 60])
print(arr)
print()
print('take,指定轴')
arr = np_random.randn(2, 4)
inds = [2, 0, 2, 1]
print(arr)
print(arr.take(inds, axis = 1)) # 按列takeFancy Indexing例子代码
[700 100 200 600]
使用take
[700 100 200 600]
使用put更新内容
[ 0 50 50 300 400 500 50 50 800 900]
[ 0 10 20 300 400 500 60 70 800 900]
take,指定轴
[[-0.24552838 -0.92345891 0.2884456 -0.01722292]
[ 1.36484709 1.35912696 0.31894399 -0.50797473]]
[[ 0.2884456 -0.24552838 0.2884456 -0.92345891]
[ 0.31894399 1.36484709 0.31894399 1.35912696]]
例题分析 距离矩阵计算
给定m * n阶矩阵X,满足X=[ x1,x2,...xn ]。求 n×n 矩阵,使得 Dij=||xi−xj||2
import numpy as np
import numpy.linalg as la
import time
X = np.array([range(0, 500), range(500, 1000)])
m, n = X.shape
print((m, n))
t = time.time()
D = np.zeros([n, n])
for i in range(n):
for j in range(i + 1, n):
D[i, j] = la.norm(X[:, i] - X[:, j]) ** 2
D[j, i] = D[i, j]
print(time.time() - t)
t = time.time()
D = np.zeros([n, n])
for i in range(n):
for j in range(i + 1, n):
d = X[:, i] - X[:, j]
D[i, j] = np.dot(d, d)
D[j, i] = D[i, j]
print(time.time() - t)
t = time.time()
G = np.dot(X.T, X)
D = np.zeros([n, n])
for i in range(n):
for j in range(i + 1, n):
D[i, j] = G[i, i] - G[i, j] * 2 + G[j,j]
D[j, i] = D[i, j]
print(time.time() - t)
t = time.time()
G = np.dot(X.T, X)
H = np.tile(np.diag(G), (n, 1))
D = H + H.T - G * 2
print(time.time() - t)(2, 500)
1.1293931007385254
0.44684743881225586
0.1688094139099121
0.0156557559967041