电路复习——动态电路的时域分析

动态电路的时域分析

[!] 以下笔记内容可能会出现部分错误的地方，恳请各位师生批评指正，谢谢！

---

主要内容

• 动态元件
• 换路定则
• 一阶动态电路的时域分析法

---

动态和稳态

• 当电路结构或元件参数发生变化时，电路中的响应与激励电源遵循相同的变化规律，电路能够马上处于稳定状态，简成稳态。
• 电路从一种稳定状态要经历一段时间后才能达到另一种稳定状态，这两种稳定状态之间的过程就成为电路的动态过程。在这中间电路电压、电流响应都是随时间而变的动态量，动态过程也称暂态过程。
• 暂态就是在动态过程中每一时刻电路的状态。

---

动态元件

• 电感和电容元件的伏安特性以微分或积分的形式来表示，所以称为动态元件。

1 电感元件

将导线绕制成线圈便构成实际的电感器，也成为电感线圈。

1.1 介绍

• 电感是一个将电能转化为磁场能并储存的元件。
• 当一个匝数为$N$的线圈通过电流$i$时，线圈之中将会建立磁场，形成磁通$\Phi (i)$。磁通穿过每匝线圈形成磁链$\psi$，有关系$$\psi =N\Phi (i)\text{\hspace{1em}(1-1-1)}$$
• 当流过电感的电流的参考方向和磁链$\psi$的参考方向满足右手螺旋定则时，两者将会成正比例关系，即$$\psi =Li\text{\hspace{1em}(1-1-2)}$$其中$L$为电感元件的电感系数或称为自感系数，简称电感。
• 对(1-1-1)与(1-1-2)两边进行微分，可以得到$$L=N\frac{d\Phi }{di}$$当$\Phi$与电流$i$成一次关系时，电感$L$为常量，这样的电感成为线性电感，属于线性元件。

1.2 伏安特性

• 由(1-1-2)可知，当电流$i$变化时，磁链$\psi$也会随之改变，变化的磁场产生感应电感，从而形成了感应电压$u$。
• 根据法拉第电磁感应定律，有$$u=\frac{d\psi }{dt}\text{\hspace{1em}(1-2-1)}$$将(1-1-2)代入(1-2-1)，有$$u=L\frac{di}{dt}\text{\hspace{1em}(1-2-2)}$$这就是电感元件的伏安特性，从公式中可得，电感的端电压是由电感电流的变化引起的。
• 在稳态电路中，由于电流不随时间变化，即$i(t)=C$，代入公式得到电感端电压为零，故在稳态电路中可以将电感视为短路。
• 假设在$(0,t]$时间内电路在动态过程，对(1-2-2)两边进行积分，有$$i(t)=\frac{1}{L}{\int }_{-\infty }^{t}u(\tau )d\tau =\frac{1}{L}{\int }_{-\infty }^{0}u(\tau )d\tau +\frac{1}{L}{\int }_0^{t}u(\tau )d\tau$$$$=i(0)+\frac{1}{L}{\int }_0^{t}u(\tau )d\tau \text{\hspace{1em}(1-2-3)}$$其中$i(0)$是在电感电流在$t=0$时的初始值。
• 由(1-2-3)可知任意时刻的电感电流不仅与该时刻的电压有关，还与初始时刻的电流有关。这种性质称为记忆性，故电感也称为记忆元件。

1.3 功率与能量

• 将(1-2-2)代入到功率公式中，有$$p=ui=Li\frac{di}{dt}\text{\hspace{1em}(1-3-1)}$$
• 对于$t_0$~$t_1$时间，能够求得电感中储存的磁场能为$$W_L={\int }_{t_0}^{t_1}pdt={\int }_{i_0}^{i_1}Lidi=\frac{1}{2}L{i}_1^2-\frac{1}{2}L{i}_0^2$$能够看出其满足势能函数的形式，即能够得到电感在$t$时刻储存的磁场能为$$W_L=\frac{1}{2}L{i}^2\text{\hspace{1em}(1-3-2)}$$
• 能够看出，电感元件存储的能量只与电流有关，且它并不像电阻一样将被转化的能量消耗掉，而是以磁场能的形式储存在电磁场里，因此我们也称电感为储能元件。

1.4 串联与并联

• 对多个串联电感的二端子网络进行分析，有$$u=\sum u_n=L_1\frac{di}{dt}+L_2\frac{di}{dt}+\cdots +L_n\frac{di}{dt}=(L_1+L_2+\cdots +L_n)\frac{di}{dt}$$与(1-2-2)进行比较，即可得到等效电感$$L_{eq}=L_1+L_2+\cdots +L_n$$
• 使用(1-2-3)与基尔霍夫电流定律可以得到并联电感的等效电感$$\frac{1}{L_{eq}}=\frac{1}{L_1}+\frac{1}{L_2}+\cdots +\frac{1}{L_n}$$

2 电容元件

电容与电感之间有着很明显的对偶性，电容中很多的内容与电感相似。

2.1 介绍

• 电容元件是一个储存电场能量的元件。
• 电容器极板上的电荷量$q$与所加的电压$u$大小成正比，有$$q=Cu\text{\hspace{1em}(2-1-1)}$$其中的比例系数$C$称为电容元件的电容量或电容。¹
• 与线性电感类似，当电容$C$是一个常数时，这样的电容称为线性电容，也是线性元件。

2.2 伏安特性

• 由电流的定义式$i=\frac{dq}{dt}$代入到(2-1-1)中，有$$i=C\frac{du}{dt}\text{\hspace{1em}(2-2-1)}$$这就是电容元件在电流和电压关联方向时的伏安特性。
• 在稳态电路中，电压不随时间的变化而改变，因此可视为开路。
• 对两边积分，可得$$u=\frac{1}{C}{\int }_{-\infty }^{t}i(\tau )d\tau =\frac{1}{C}{\int }_{-\infty }^{0}i(\tau )d\tau +\frac{1}{C}{\int }_0^{t}i(\tau )d\tau$$$$=u(0)+\frac{1}{C}{\int }_0^{t}i(\tau )d\tau \text{\hspace{1em}(2-2-2)}$$其中$u(0)$是电容电压在$t=0$时的初始值。
• 由(2-2-2)可知，任意时刻的电容电压不仅仅于当前的电压有关，还与初始时刻的电压有关。这种性质称为记忆性，故电容也称为记忆元件。

2.3 功率与能量

• 将(2-2-1)代入到功率定义式中，有$$p=ui=Cu\frac{du}{dt}\text{\hspace{1em}(2-3-1)}$$
• 在$t_0$~$t_1$时间中可以求得电容储存的电场能为$$W_C={\int }_{t_0}^{t_1}pdt={\int }_{t_0}^{t_1}Cu\frac{du}{dt}dt={\int }_{u_0}^{u_1}Cudu=\frac{1}{2}C{u}_1^2-\frac{1}{2}C{u}_0^2$$能够看出与电感的形式很相似，即电容在$t$时刻储存的电场能为$$W_C=\frac{1}{2}C{u}^2\text{\hspace{1em}(2-3-2)}$$
• 电容储存的磁场能只与当前时刻的电容电压有关，电容在转换过程中没有能量的损耗，所以电容元件也是储能元件。

2.4 串联与并联

• 对于多个电容并联形成的二端口网络进行分析，有$$i=C_1\frac{du}{dt}+C_2\frac{du}{dt}+\cdots +C_n\frac{du}{dt}=(C_1+C_2+\cdots +C_n)\frac{du}{dt}\text{\hspace{1em}(2-4-1)}$$
• 将(2-2-1)与(2-4-1)进行对比，即可得到电容并联的等效电容$$C_{eq}=C_1+C_2+\cdots +C_n$$
• 使用(2-1-1)与基尔霍夫电压定律即可得到串联电感的等效电感$$\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\cdots +\frac{1}{C_n}$$

---

换路定则

1 换路

• 当电路结构或者电路元件参数发生了变化的时候，电路会从一种工作状态转变到另一种工作状态，这就是换路。
• 换路实际上就是电路的工作状态发生改变。
• 由(1-3-1)与(2-3-1)可得，当时间趋于零时（即瞬间换路时），电感和电容的功率无限大，这显然是违反能量守恒的。
• 因此在换路时，若电路中含有电容、电感这些储能元件时，电路无法发生突变（即在瞬间完成换路），因此在这个时候电路从换路时要经过一个过程后才能到达新的稳态，这个过程我们称之为过渡过程或暂态过程。

2 换路定则

• 由(1-3-2)可知，电感的能量只与它的电流有关，磁场能量不能突变意味着电感的电流$i_L$不能突变。
• 由(2-3-2)可知，电容的能量只与它的电压有关，电场能量不能突变意味着电容的电压$u_C$不能突变。
• 综上所述，在换路瞬间，电容元件的电流值为有限值时，其电压$u_C$不能突变；电感元件的电压值为有限值时，其电流$i_L$也不能突变。这个结论称为换路定则。用公式表示为
  $$\{\begin{array}{l}{i}_L(0_{+})=i_L(0_{-})\\ u_C(0_{+})=u_C(0_{-})\end{array}$$它表示在换路前后，即从$t=0_{-}$到$t=0_{+}$瞬间，若电感电压和电容电流为有限值，则电容元件的电压与电感元件的电流在该时刻连续，不会发生突变。
• 换路定则只适用于换路的瞬间。

3 初始值的确定

• 假设我们电路仅在$t=0$时刻发生了换路。

3.1 $t=0_{-}$

• 在这个时候电路还没有发生换路，还是处于上一个稳态阶段。因此我们可以采取将电容开路，将电感短路的手段得到一个等效的电阻电路，对这个电路进行分析即可得到各支路上确定的值。

3.2 $t=0_{+}$

• 这时电路刚刚发生了换路，由换路定则可知
  $$\{\begin{array}{l}{i}_L(0_{+})=i_L(0_{-})\\ u_C(0_{+})=u_C(0_{-})\end{array}$$
  因此只需要采取将电容换成电压值为$u_C(0_{-})$的恒压源，将电感换成电流值为$i_L(0_{-})$的恒流源得到换路后瞬间的等效的电阻电路，对这个电路进行分析即可以得到各支路上确定的值。

3.3 注意

• 换路瞬间电容电压和电感电流不能突变，但是电容电流和电感电压却可以。

---

一阶动态电路的时域分析法

• 只含有一个储能元件或经过等效变换后也只含有一个储能元件的线性电路，称为一阶线性电路。
• 一阶线性电路的电流或电压关系都可以用一阶线性常系数微分方程来表示。

1 一阶动态电路微分方程的建立

• 根据储能元件的不同，一阶动态电路分为一阶RC电路和一阶RL电路。

1.1 一阶RC电路

• 当储能元件为电容时，一阶动态电路即为一阶RC电路。
  

1.1.1 推导

• 由换路定则可知，换路前后的电容电压为连续值。
• 假设电路在且仅在$t=0$时刻发生了一次换路（开关闭合），故有$$u_C(0_{-})=u_C(0_{+})=U_0$$其中$U_0$为开关闭合前的电容电压.
• 在开关闭合后，由换路定则和基尔霍夫电压定律可得$$E=u_R+u_C$$代入各元件的伏安特性，有$$E=RC\frac{d{u}_C}{dt}+u_C\text{\hspace{1em}(2-1-1)}$$这是一个一阶线性常系数微分方程。
• 对于一般的一阶常系数微分方程可以得到如下解的形式$$u_C=u_C^{\prime }+u_C^{\prime \prime }\text{\hspace{1em}(2-1-2)}$$其中$u_C^{\prime }$称为非齐次微分方程的特解，$u_C^{\prime \prime }$称为齐次微分方程的通解。
• 其中该方程的特解满足(2-1-1)，因此使用极限思想，当$t=\infty$时，电路处于另一个稳定状态，此时进行分析，有$$u_C(\infty )=E=u_C^{\prime }$$能够看出，特解不随时间的变化而变化，是稳定值，因此也称为稳态分量。²
• 对于通解$u_C^{\prime \prime }$的一般形式有$$u_C^{\prime \prime }=A{e}^{pt}$$代入到$$RC\frac{d{u}_C}{dt}+u_C=0$$中，有$$RCpA{e}^{pt}+A{e}^{pt}=0$$即有$$(RCp+1)A{e}^{pt}=0$$因为$A{e}^{pt}\ne 0$，所以有$$RCp+1=0$$解得$$p=-\frac{1}{RC}=-\frac{1}{\tau }$$其中$\tau$称为电路的时间常数，单位为秒，反映了电路暂态过程的快慢，即换路后电路达到新的稳定状态所需时间的长短。
• 因此特解为$$u_C^{\prime \prime }=A{e}^{-\frac{t}{\tau }}$$与通解一起代入到(2-1-2)，有$$u_C(t)=u_C(\infty )+A{e}^{-\frac{t}{\tau }}$$令$t=0_{+}$，即有$$u_C(0_{+})=u_C(\infty )+A{e}^{-\frac{0}{\tau }}=u_C(\infty )+A$$解得$$A=u_C(0)-u_C(\infty )$$

1.1.2 公式

• 综上所述，一阶RC电路的一阶常系数微分方程解为$$u_C(t)=[u_C(0)-u_C(\infty )]e^{-\frac{t}{\tau }}+u_C(\infty ),t\ge 0$$
• 将该解作为已知量进行电路分析，即可得到电路中其他的电流电压响应。

1.2 一阶RL电路

• 当储能元件为电感时，一阶动态电路即为一阶RL电路。³
  

1.2.1 推导

• 由换路定则可知，换路前后的电感电流为连续值。
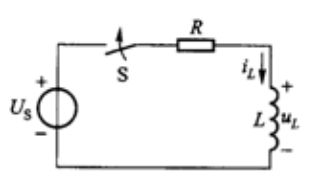
• 假设电路在且仅在$t=0$时刻发生了一次环路（开关闭合），故有$$i_L(0_{-})=i_L(0_{+})$$对电路列基尔霍夫电压方程，有$$U_s=u_R+u_L$$代入各元件的伏安特性关系，有$$\frac{L}{R}\frac{d{i}_L}{dt}+i_L=\frac{U_s}{R}\text{\hspace{1em}(2-2-1)}$$
• 与一阶RC电路同理，有解的形式为$$i_L(t)=i_L^{\prime }+i_L^{\prime \prime }\text{\hspace{1em}(2-2-2)}$$其中特解$i_L^{\prime }$使用极限思想后有$$i_L^{\prime }=\frac{U_S}{R}$$
• 对于通解，有形式$$i_L^{\prime \prime }=A{e}^{pt}$$将其代入(2-2-1)对应的齐次方程，有$$\frac{L}{R}pA{e}^{pt}+A{e}^{pt}=0$$由于$A{e}^{pt}\ne 0$，解得$$p=-\frac{R}{L}=-\frac{1}{\tau }$$其中$\tau$为时间常数。
• 代入到(2-2-2)，有$$i_L(t)=A{e}^{-\frac{t}{\tau }}+\frac{U_s}{R}$$令$t=0$，得$$A=i_L(0)-\frac{U_s}{R}=i_L(0)-i_L(\infty )$$

1.2.2 公式

• 综上所述，一阶RL电路的一阶常系数微分方程解为$$i_L(t)=[i_L(0)-\frac{U_s}{R}]e^{-\frac{t}{\tau }}+\frac{U_s}{R},t\ge 0$$
• 将该解作为已知量进行电路分析，即可得到电路中其他的电流电压响应

2 三要素分析法

• 对比一阶RC电路与一阶RL电路的解，能够得到一个一般形式$$f(t)=[f(0)-f(\infty )]e^{-\frac{t}{\tau }}+f(\infty ),t\ge 0$$其中$f(t)$为一阶电路中任意响应随时间的变化,$f(0)$a为换路瞬间(可以看作换路前)的响应，$f(\infty )$为换路后另一稳态的响应，$\tau$为时间常数。
• 只要我们得到$f(0)$、$f(\infty )$、$\tau$这三个要素，我们就能得到在直流激励电源的作用下一阶电路动态过程中的电流电压响应。

2.1 步骤

• 可以按照如下步骤来求得三个要素：
  1. 确定初始条件$u_C(0_{+})$或$i_L(0_{+})$
  2. 确定初始值$f(0_{+})$
  3. 确定稳态值$f(\infty )$
  4. 确定时间常数$\tau$
  5. 求一阶线性电路的动态响应

2.2 提醒

• 对于一阶RC电路，时间常数为$$\tau =RC$$
• 对于一阶RL电路，时间常数为$$\tau =\frac{L}{R}$$
• 三要素分析法只适用于只含有一个储能元件或能等效为一个储能元件的一阶线性电路动态过程的分析，而不适用于含有两个或以上储能元件的二阶或高阶的电路的动态分析。

2.3 改进

• 若直接求$u_C(t)$与$i_L(t)$，再用这些作为已知量直接对电路进行分析，可以省略掉步骤2。

---

1. 电容和其符号$C$既代表了电容元件，也代表了电容元件的参数——电容。 ↩︎

2. 若是电压源的电压值发生改变而产生的换路，这个特解等于改变后的电压源电压值，也是稳定不变的。 ↩︎

3. 两图都来自于中国电工考试网，虽然不知道为啥它的表述是不一样的。 ↩︎