Vincent19999999

几何入门合集 gym101968 problem F. Mirror + gym102082 Problem F Fair Chocolate-Cutting + gym101915 problem ...

abstract:

V const & a 加速

F. Mirror

题意

链接

问题：
有n个人在y=0的平面上(及xoz平面)。z=0平面上有一面镜子(边平行于坐标轴）。z=a平面上有q个点（保证a大于所有人的z坐标）。所有人面朝镜子，且在镜子和q个点之间（即每个人的z坐标保证0 问对于某个点，让所有人能够通过镜子看到那个点的镜子的最小面积。

题解

三维几何+镜像+凸包
首先考虑镜面，我们可以通过（初中科学的）镜面反射原理，关于z=0做出z=a的对称平面z=-a。问题就变成了n个人看z=-a上的某个点。(下图绿点是人，红点是询问点)

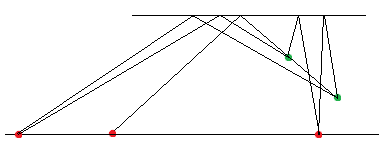
然后观察，镜子的高和宽是独立的。于是我们分别求它们的最大值即可。
求高比较简单，我们朝-x方向看yoz平面。通过把每个人跟点Q的像Q‘相连，我们发现离Q’z轴距离最近的人对应着镜子的下边界，最远的人对应着上边界，通过维护所有人z坐标的max_z&min_z以及相似三角形可以直接求出两个边界，复杂度为O(1)。
我们用同样的方法，朝-y方向看xoz平面。通过把每个人跟点Q的像Q‘相连，我们发现，左右边界并不对应着最左边与最右边的人。而且随着询问点的变化，对应着左右边界的人也在变化。
如果我们暴力的找对应左右边界的人，复杂度为n*q ,不可行。
我们发现，对应着左右边界的人虽然随着询问点变化，但他们都在凸包上(如下图)。

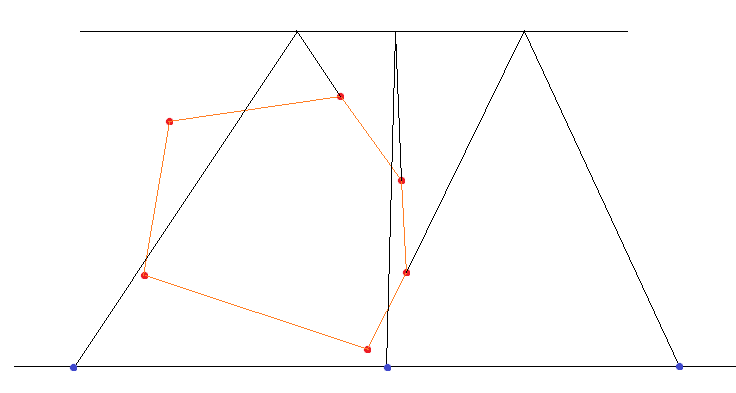
更进一步，如果我们将询问点按照x坐标排序，随着询问的x坐标增加，左右边界的人在凸包上的变化是顺时针旋转的。（考虑你从左到右观察一个正前方的凸包）
于是我们就能够通过一个nlogn的凸包预处理然后O(1)地回答每个询问，复杂度为O(q+nlogn)

剩下的是实现”从左到右看凸包时凸包左右边界的顺时针更新“。
首先是写out，in函数（右手法则，向外转就是逆时针），用来逆时针、顺时针遍历凸包上的点。因为极角排序凸包存的点是逆时针的(极角排序的那个角是与y轴的逆时针夹角。)，所以out就是++。
先找到凸包的下上顶点，作为初始的左右边界的对应点。
然后根据x坐标从小到大枚举询问点Q。
对于每个Q，不断顺时针更新左边界对应的人，直到他与Q的连线在他凸包上顺时针的下一个人与Q的连线的外面(直观上显然正确)。右边界同理。
某些编辑器比如codeforces不能混用iostream与stdio

代码

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define debug(x) cerr<<#x<<" = "<<(x)< Q[maxn];
bool cmpr(V const &a, V const &b) {
    V v1 = a - st[0], v2 = b - st[0];
    return (v1 | v2) < -eps;
}

vector ch;
void getCH() {
    sort(st + 1, st + n, cmpr);
    ch.push_back(st[0]);
    rep(i, 1, n-1) {
        while (ch.size() > 1 && (st[i] - ch.back() | ch.back() - ch[ch.size() - 2]) < eps)ch.pop_back();
        ch.push_back(st[i]);
    }
}
int out(int x) { return x ? x - 1 : ch.size() - 1; }
int in(int x) { return x + 1 == (int)ch.size() ? 0 : x + 1; }


double getx(double xs, double z, double xq) {
    return xs + z / (z + a) * (xq - xs);
}



int main() {
    //FAST_IO;
    int t;
    cin >> t;
    while (t--) {

        cin >> n >> a;
        
        rep(i, 0, n - 1)st[i].sc();
        db zmn = st[0].y, zmx = st[0].y;
        rep(i, 0, n - 1) {
            zmn = min(zmn, st[i].y);
            zmx = max(zmx, st[i].y);
        
        }
        rep(i, 0, n - 1)st[i].y = a - st[i].y;
        sort(st, st + n);
        ch.clear();
        getCH();

        cin >> q;
        ll qx = 0, qy = 0;
        rep(i, 1, q) {
            Q[i].first.sc();
            Q[i].second = i;
        }
        sort(Q + 1, Q + 1 + q);

        int lp = 0, rp = 0;
        rep(i, 0, ch.size() - 1)ch[i].y = a - ch[i].y;
        while (ch[in(rp)].y < ch[rp].y)rp = in(rp);
        while (ch[out(lp)].y > ch[lp].y)lp = out(lp);

        rep(i, 1, q) {
            while (true) {
                int ni = in(lp);
                if (getx(ch[ni].x, ch[ni].y, Q[i].first.x) < getx(ch[lp].x, ch[lp].y, Q[i].first.x))lp = ni;
                else break;
            }
            while (true) {
                int ni = in(rp);
                if (getx(ch[ni].x, ch[ni].y, Q[i].first.x) > getx(ch[rp].x, ch[rp].y, Q[i].first.x))rp = ni;
                else break;
            }
            double x = abs(getx(ch[rp].x, ch[rp].y, Q[i].first.x) - getx(ch[lp].x, ch[lp].y, Q[i].first.x));
            double h = getx(0, zmx, Q[i].first.y) - getx(0, zmn, Q[i].first.y);
            ans[Q[i].second] = (long double)x * h;
            //printf("%.20lf\n", x*h);
        }
        rep(i, 1, q)printf("%.20lf\n", (double)ans[i]);
    }
    cin >> n;
}

/*
1
3 3
-2 1
7 2
3 1
3
2 5
-2 4
8 10
*/

心路历程

当有两个以上的bug时你就炸了
wa0:FAST_IO codeforces以用就wa

wa1:输出rep(i,1,q) not rep(i,1,n)//最后才发现
wa2：凸包板子里面下标从0开始。

Problem F Fair Chocolate-Cutting

题意

来源：ICPC Asia Regional Contest, Yokohama, 2018–12–09

让你求所有平分凸多边形的线段中最长和最短的那两条。
输出它们的长度。
---

题解

证明题+硬核平面几何
我们有结论：（目前不会证明）
某合法（平分多边形的）线段的端点在顶点上时一定是局部最长或最短的。
除此之外，当某合法线段垂直于任意“外角”平分线时，也是局部最短的

于是问题就转化成
1.对于每个顶点，找到过它的合法线段。

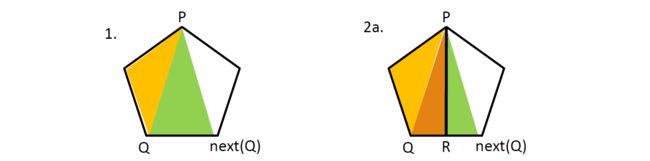
2.对于每个角（跳过一些线段的“相邻”两条线段的延长线交出的角）,找到垂直它的平分线的合法线段。注意特判掉角不存在的情况，即两边平行。

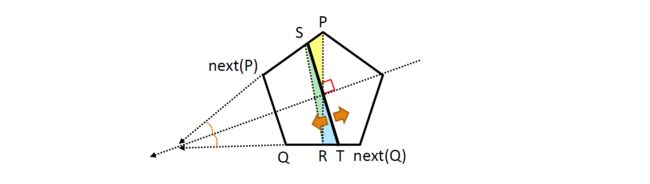
对于1，只要从该顶点开始不断逆时针扫顶点，直到刚刚超过1/2的总面积。然后把上一个三角形分割一下。
对于2，直接用平面几何知识以及三角函数求解
---

代码

#include
#include 
#include 
#include 
#include 
#include 
#include
#include
typedef long long ll;
typedef double db;
typedef long double ld;

using namespace std;
typedef complex  point;
#define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++)
#define F(i,N)for(int i = 0;i < (int)(N);i ++)
#define Decimal fixed< V;
double sumS,nowS,mx,mn;
double cross(const point& a, const point& b) {
    return imag(conj(a)*b);
}
double dot(const point& a, const point& b) {
    return real(conj(a)*b);
}
double area(const vector& p) {
    double A = 0;
    F(i, p.size()) A += cross(curr(p, i), next(p, i));
    return A / 2.;
}
double triArea(int a, int b, int c) {
    a %= n, b %= n, c %= n;
    if (a == b || b == c || c == a)return 0;
    vector tmp = { V[a],V[b],V[c] };
    return area(tmp);
}
double distancePP(point const &a, point const &b) {
    return abs(a - b);
}
//seg
struct segment :public vector {
    segment(const point &a, const point &b) {
        push_back(a); push_back(b);
    }
};
point crosspoint(segment const &l,segment const &m) {
    double A = cross(l[1] - l[0], m[1] - m[0]);
    double B = cross(l[1] - l[0], l[1] - m[0]);
    if (abs(A) < eps&&abs(B) < eps)return m[0];//same line
    if (abs(A) < eps)return point(INF, INF);//parallel
    return m[0] + B / A*(m[1] - m[0]);
}
double angle(const point& a, const point& b) {
    auto tmp = abs(arg(a) - arg(b));
    return min(tmp, 2 * PI - tmp);
}
double angle(const segment &s1, const segment &s2) {
    return angle(s1[1] - s1[0], s2[1] - s2[0]);
}
point projection(const segment &l, const point &p) {
    double t = dot(p - l[0], l[0] - l[1]) / norm(l[0] - l[1]);
    return l[0] + t * (l[0] - l[1]);
}
double distanceLP(const segment &l, const point &p) {
    return abs(p - projection(l, p));
}
bool intersectSP(const segment &s,const point &p) {//point on seg
    return abs(s[0] - p) + abs(s[1] - p) - abs(s[1] - s[0]) < eps;
}
double seica(int a,int b) {
    a %= n; b %= n;
    vector tmp;
    int i = a;
    while (1) {
        tmp.EB(V[i]);
        if (i == b)break;
        i = (i + 1) % n;
    }
    if (tmp.size() < 3)return 0;
    else return area(tmp);
}
void checkV(int p,int q) {
    p %= n; q %= n;
    double remain = (sumS / 2) - nowS;
    double rate = remain / triArea(p, q, q + 1);
    point tmp = V[q] + rate * (V[(q + 1) % n] - V[q]);
    mn = min(mn, distancePP(V[p], tmp));
    mx = max(mx, distancePP(V[p], tmp));
}
void checkSeg(int p, int q) {
    p %= n, q %= n;
    nowS -= triArea(p, p + 1, q);
    segment a(V[(p + 1) % n], V[p]);
    segment b(V[(q) % n], V[(q + 1) % n]);
    point crossp = crosspoint(a, b); 
    if (crossp == point(INF, INF)) {
        double sqS = area({ V[p],V[(p + 1) % n],V[q],V[(q + 1) % n] });
        if (nowS + sqS < sumS / 2 + eps)return;
        bool flag = 0;
        if (intersectSP(b, projection(b, a[0])) || intersectSP(b, projection(b, a[1])))flag = 1;
        if (intersectSP(a, projection(a, b[0])) || intersectSP(a, projection(a, b[1])))flag = 1;
        if (!flag)return;
        mn = min(mn, distanceLP(b, a[0]));
        return;
    }
    double tmpS=0;
    if (distancePP(crossp, a[0]) > distancePP(crossp, a[1]) + eps) {
        tmpS = seica(q + 1, p);
        swap(a[0], a[1]);
        swap(b[0], b[1]);
    }
    else {
        tmpS= seica(p + 1, q);
    }
    double theta = angle(a, b);
    double T = distancePP(crossp, a[0])*distancePP(crossp, b[0])*sin(theta) / 2;
    double leg = (2 * (T - tmpS) + sumS) / sin(theta);
    bool flag = 0;
    if (leg > distancePP(a[1], crossp)*distancePP(a[1], crossp) + eps)flag = 1;
    if (leg + eps < distancePP(a[0], crossp)*distancePP(a[0], crossp))flag = 1;
    if (leg > distancePP(b[1], crossp)*distancePP(b[1], crossp) + eps)flag = 1;
    if (leg + eps < distancePP(b[0], crossp)*distancePP(b[0], crossp))flag = 1;
    if (flag)return;
    mn = min(mn, 2*sqrt(leg)*sin(theta / 2));
}
int main() {
    mx = 0;
    mn = 1e18;
    cin >> n;
    F(i, n) {
        db a, b;
        cin >> a >> b;
        V.EB(a, b);
    }
    int q = 1;
    sumS = area(V);
    F(i, n) {
        while (nowS + triArea(i, q, q + 1) < sumS / 2 + eps) {
            nowS += triArea(i, q, q + 1);
            q++;
        }
        checkV(i,q);
        checkSeg(i,q);
    }
    cout << Decimal << mn << endl;
    cout << Decimal << mx << endl;
    cin >> n;
    return 0;
}






/*
4
0 0
10 0
10 10
0 10


3
0 0
6 0
3 10
*/

心路历程


关键是不会证明。  
复数大法好啊！！！(其实还是慢5倍？？下面那题)

B. Ali and Wi-Fi

题意

来源ACM International Collegiate Programming Contest, Tishreen Collegiate Programming Contest
100个圆，每个圆代表wifi覆盖区域，每个wifi有一个网速。你最多可以连入m个WiFi，网速为这些wifi的总和。
问你最大的网速是多少。

题解

想法题+圆模板
我们知道n个圆最多可以把平面分成n^2-n+2个区域(递推进阶题233)。所以可以考虑遍历每个区域，计算它被哪些圆。。。
我们发现维护一块区域很难，而要取最大的m个更难考虑。
于是考虑维护圆与圆的交点。我们发现每个区域都是圆交出来的，i.e.交点都在区域的边界上。
于是我们可以枚举交点来代替枚举区域，显然交点个数也是n^2级别的。(考虑圆内含的情况，所以要把每个圆心也枚举一遍)
这样枚举的另一个好处是可以很简单地处理m：
枚举每个交点，计算有几个圆包含它。然后直接在这些圆中取最大的m个。
复杂度为n^2nnlogn。
如果我们用优先队列来维护最大的m个，那么复杂度里可以去掉一个n。

代码

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define debug(x) cerr<<#x<<" = "<<(x)< point;
#define X real()
#define Y imag()
const int maxn = 2e5 + 5;
const db eps = 1e-10;
const db PI = acos(-1.);
int dcmp(ld x)
{
    if (fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}
struct V {
    ld x, y;
    V() {}
    void sc() { scanf("%lf%lf", &x, &y); }
    V(double a, double b) : x(a), y(b) { }
    V operator+(const V &o)const { return V(x + o.x, y + o.y); }
    V operator-(const V &o)const { return V(x - o.x, y - o.y); }
    double L() { return sqrt(x * x + y * y); }
    V N() {
        double l = L();
        return V(x / l, y / l);
    }
    V rot(double th) { return V(x * cos(th) - y * sin(th), x * sin(th) + y * cos(th)); }
    V operator*(double z) { return V(x * z, y * z); }
    double operator*(const V &o) const { return x * o.x + y * o.y; }
    double operator|(const V &o) const { return x * o.y - o.x * y; }
    double operator==(const V &o) const { return dcmp(x - o.x) == 0 && dcmp(y - o.y) == 0; }
    void pr() { printf("%lf %lf\n", x, y); }
};
vector p;
typedef V point;
V conj(V p) { return V(p.x, -p.y); }
double arg(V p) { return atan2(p.y, p.x); }
double norm(V p) { return p.L()*p.L(); }
double abs(V p) { return p.L(); }



double cross(const point& a, const point& b) {
    return imag(conj(a)*b);
}
double dot(const point& a, const point& b) {
    return real(conj(a)*b);
}
struct circle
{
    point c;
    ld r, v;
    circle() {}
    circle(point c, ld r, ld v) :c(c), r(r), v(v) {}

    inline point pt(double a)
    {
        return point(c.x + cos(a)*r, c.y + sin(a)*r);
    }
};
int getCircleCircleIntersection(circle C1, circle C2, point &t1, point &t2)
{
    ld d = abs(C1.c - C2.c);
    if (dcmp(d) == 0)
    {
        if (dcmp(C1.r - C2.r) == 0) return -1;// same cir
        return 0;// include
    }
    if (dcmp(C1.r + C2.r - d) < 0) return 0;// disjoint
    if (dcmp(fabs(C1.r - C2.r) - d) > 0) return 0;// include
    ld a = arg(C2.c - C1.c);
    ld da = acos((C1.r*C1.r + d * d - C2.r*C2.r) / (2 * C1.r*d));
    point p1 = C1.pt(a - da), p2 = C1.pt(a + da);
    t1 = p1;
    if (p1 == p2) return 1;
    t2 = p2;
    return 2;
}
vector A;
circle aa[105];
vector P;
point pp[10105];
priority_queue Q;
int  ans, sum;
int n, m, tot;
int main() {
    FAST_IO;
    int t;

    cin >> t;
    while (t--) {

        tot = ans = 0;
        cin >> n >> m;
        F(i, n) {

            cin >> aa[i].c.x >> aa[i].c.y >> aa[i].r >> aa[i].v;

        }
        F(i, n) {
            rep(j, i + 1, n - 1) {
                point t1, t2;
                int num = getCircleCircleIntersection(aa[i], aa[j], t1, t2);
                if (num == 1) {
                    pp[tot++] = t1;
                }
                else if (num == 2) {
                    pp[tot++] = t1;
                    pp[tot++] = t2;
                }
            }
        }
        F(i, n)pp[tot++] = aa[i].c;
        F(j, tot) {
            F(i, n) {
                if (dcmp(abs(pp[j] - aa[i].c) - aa[i].r) <= 0) {
                    Q.push(-aa[i].v);
                    if (Q.size() > m)Q.pop();
                }
            }
            sum = 0;
            while (!Q.empty()) {
                sum -= Q.top();
                Q.pop();
            }
            ans = max(ans, sum);
        }
        cout << ans << endl;
    }
    cin >> t;
    return 0;
}

心路历程

没初始化。
瞎debug发现long double int求和会爆精度。
priority_Q太久没用，忘记pop是从头上弹出的了orz。
vector 和对于1e6的数据其实只比数组慢10ms。

转载于:https://www.cnblogs.com/SuuT/p/10669811.html

第四天旅游线路预览——从换乘中心到喀纳斯湖陟彼高冈yu 基于Google earth studio 的旅游规划和预览旅游
第四天：从贾登峪到喀纳斯风景区入口，晚上住宿贾登峪；换乘中心有4路车，喀纳斯①号车，去喀纳斯湖，路程时长约5分钟；将上面的的行程安排进行动态展示，具体步骤见”Googleearthstudio进行动态轨迹显示制作过程“、“Googleearthstudio入门教程”和“Googleearthstudio进阶教程“相关内容，得到行程如下所示：Day4-2-480p
linux中sdl的使用教程,sdl使用入门 Melissa Corvinus linux中sdl的使用教程
本文通过一个简单示例讲解SDL的基本使用流程。示例中展示一个窗口，窗口里面有个随机颜色快随机移动。当我们鼠标点击关闭按钮时间窗口关闭。基本步骤如下：1.初始化SDL并创建一个窗口。SDL_Init()初始化SDL_CreateWindow()创建窗口2.纹理渲染存储RGB和存储纹理的区别：比如一个从左到右由红色渐变到蓝色的矩形，用存储RGB的话就需要把矩形中每个点的具体颜色值存储下来；而纹理只是一
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
2022现在哪个打车软件比较好用又便宜实惠的打车软件合集高省APP珊珊
这是一个信息高速传播的社会。信息可以通过手机，微信，自媒体，抖音等方式进行传播。但同时这也是一个交通四通发达的社会。高省APP，是2022年推出的平台，0投资，0风险、高省APP佣金更高，模式更好，终端用户不流失。【高省】是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，也期待你的加入。珊珊导师，高省邀请码777777，注册送2皇冠会员，送万元推广大礼包，教你如何1年做到百万团队。高
Faiss Tips：高效向量搜索与聚类的利器焦习娜Samantha
FaissTips：高效向量搜索与聚类的利器faiss_tipsSomeusefultipsforfaiss项目地址:https://gitcode.com/gh_mirrors/fa/faiss_tips项目介绍Faiss是由FacebookAIResearch开发的一个用于高效相似性搜索和密集向量聚类的库。它支持多种硬件平台，包括CPU和GPU，能够在海量数据集上实现快速的近似最近邻搜索（AN
C++菜鸟教程 - 从入门到精通第二节 DreamByte c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
《我的青葱岁月之缘来是你》第二章迎新晚会思源思缘思怨
“怎么你也来了这里？”我愉快的问到，想着这是上天给的缘分吗？我还没去找他竟然就相遇了。那个让我开心的老乡。“你好，我也是舞蹈社的新人啊！”他说，笑起来回答我，眼睛弯弯的。“这么巧，我叫吴倩，你叫啥？”“我叫韩欢，你也是B市人吧，c中毕业的？”“我不是，我是f中的，不然肯定会认识你的”“是吗？以后多多关照了”他还冲我眨了眨眼睛。内心一阵悸动，这是……回到寝室，我兴奋的告诉我的室友这个事情，我再次觉得
STM32中的计时与延时 lupinjia STM32 stm32 单片机
前言在裸机开发中，延时作为一种规定循环周期的方式经常被使用，其中尤以HAL库官方提供的HAL_Delay为甚。刚入门的小白可能会觉得既然有官方提供的延时函数，而且精度也还挺好，为什么不用呢？实际上HAL_Delay中有不少坑，而这些也只是HAL库中无数坑的其中一些。想从坑里跳出来还是得加强外设原理的学习和理解，切不可只依赖HAL库。除了延时之外，我们在开发中有时也会想要确定某段程序的耗时，这就需要
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
2024.9.6 Python，华为笔试题总结，字符串格式化，字符串操作，广度优先搜索解决公司组织绩效互评问题，无向图 RaidenQ python 华为 leetcode 算法力扣广度优先无向图
1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
2019考研 | 西交大软件工程笔者阿蓉
本科背景：某北京211学校电子信息工程互联网开发工作两年录取结果：全日制软件工程学院分数：初试350+复试笔试80+面试85+总排名：100+从五月份开始脱产学习，我主要说一下专业课和复试还有我对非全的一些看法。【数学100+】张宇，张宇，张宇。跟着张宇学习，入门视频刷一遍，真题刷两遍，错题刷三遍。书刷N多遍。从视频开始学习，是最快的学习方法。5-7月份把主要是数学学好，8-9月份开始给自己每个周
(158)时序收敛---＞(08)时序收敛八 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛八（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(159)时序收敛---＞(09)时序收敛九 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛九（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(160)时序收敛---＞(10)时序收敛十 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛十（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
(153)时序收敛---＞(03)时序收敛三 FPGA系统设计指南针 FPGA系统设计(内训)fpga开发时序收敛
1目录（a）FPGA简介（b）Verilog简介（c）时钟简介（d）时序收敛三（e）结束1FPGA简介（a）FPGA（FieldProgrammableGateArray）是在PAL（可编程阵列逻辑）、GAL（通用阵列逻辑）等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。（b）F
esp32开发快速入门 8 : MQTT 的快速入门，基于esp32实现MQTT通信 z755924843 ESP32开发快速入门服务器网络运维
MQTT介绍简介MQTT（MessageQueuingTelemetryTransport，消息队列遥测传输协议），是一种基于发布/订阅（publish/subscribe）模式的"轻量级"通讯协议，该协议构建于TCP/IP协议上，由IBM在1999年发布。MQTT最大优点在于，可以以极少的代码和有限的带宽，为连接远程设备提供实时可靠的消息服务。作为一种低开销、低带宽占用的即时通讯协议，使其在物联
Armv8.3 体系结构扩展--原文版代码改变世界ctw ARM-TEE-Android armv8 嵌入式 arm架构安全架构芯片 Trustzone Secureboot
快速链接:.ARMv8/ARMv9架构入门到精通-[目录]付费专栏-付费课程【购买须知】:个人博客笔记导读目录(全部)TheArmv8.3architectureextensionTheArmv8.3architectureextensionisanextensiontoArmv8.2.Itaddsmandatoryandoptionalarchitecturalfeatures.Somefeat
python怎么将png转为tif_png转tif weixin_39977276
发国外的文章要求图片是tif，cmyk色彩空间的。大小尺寸还有要求。比如网上大神多，找到了一段代码，感谢！https://www.jianshu.com/p/ec2af4311f56https://github.com/KevinZc007/image2Tifimportjava.awt.image.BufferedImage;importjava.io.File;importjava.io.Fi
python批量读取tiff文件_Python Pillow批量转换tif格式到jpg weixin_39557797
最近因为想要整下网站的壁纸，从网站下载了别人整理好的合集压缩包，解压之后，却发现里面的文件都是tif的，tif格式网站和电脑都不认的，根本不能作壁纸。这时候，就需要转换图片格式了，首先我找了几款转换格式的软件，发现效果都不好，要不是不支持tif格式，要不就是转换出来的图片糊的不行。最终，还是决定用Python的Pillow库来写一个脚本，完成这个任务。下面是整个的小脚本----importosim
Python入门之Lesson2:Python基础语法小熊同学哦 Python入门课程 python 开发语言算法数据结构青少年编程
目录前言一.介绍1.变量和数据类型2.常见运算符3.输入输出4.条件语句5.循环结构二.练习三.总结前言欢迎来到《Python入门》系列博客的第二课。在上一课中，我们了解了Python的安装及运行环境的配置。在这一课中，我们将深入学习Python的基础语法，这是编写Python代码的根基。通过本节内容的学习，你将掌握变量、数据类型、运算符、输入输出、条件语句等Python编程的基础知识。一.介绍1
摄影小白，怎么才能拍出高大上产品图片？是波妞唉
很多人以为文案只要会码字，会排版就OK了！说实话，没接触到这一行的时候，我的想法更简单，以为只要会写字就行！可是真做了文案才发现，码字只是入门级的基本功。一篇文章离不开排版、配图，说起来很简单！从头做到尾你就会发现，写文章用两个小时，找合适的配图居然要花掉半天的时间，甚至更久！图片能找到合适的就不怕，还有找不到的，比如产品图，只能亲自拍。拿着摆弄了半天，就是拍不出想要的效果，光线不好、搭出来丑破天
2021 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级C++语言试题（第三大题：完善程序代码） mmz1207 c++csp
最近有一段时间没更新了，在准备CSP考试，请大家见谅。（1）有n个人围成一个圈，依次标号0到n-1。从0号开始，依次0，1，0，1...交替报数，报到一的人离开，直至圈中剩最后一个人。求最后剩下的人的编号。#includeusingnamespacestd;intf[1000010];intmain(){intn;cin>>n;inti=0,cnt=0,p=0;while(cnt#includeu
Vue( ElementUI入门、vue-cli安装) m0_l5z elementui vue.js
一.ElementUI入门目录：1.ElementUI入门1.1ElementUI简介1.2Vue+ElementUI安装1.3开发示例2.搭建nodejs环境2.1nodejs介绍2.2npm是什么2.3nodejs环境搭建2.3.1下载2.3.2解压2.3.3配置环境变量2.3.4配置npm全局模块路径和cache默认安装位置2.3.5修改npm镜像提高下载速度2.3.6验证安装结果3.运行n
Spring MVC 全面指南：从入门到精通的详细解析一杯梅子酱技术栈学习 spring mvc java
引言：SpringMVC，作为Spring框架的一个重要模块，为构建Web应用提供了强大的功能和灵活性。无论是初学者还是有一定经验的开发者，掌握SpringMVC都将显著提升你的Web开发技能。本文旨在为初学者提供一个全面且易于理解的学习路径，通过详细的知识点分析和实际案例，帮助你快速上手SpringMVC，让学习过程既深刻又高效。一、SpringMVC简介1.1什么是SpringMVC？Spri
入门MySQL——查询语法练习 K_un
前言：前面几篇文章为大家介绍了DML以及DDL语句的使用方法，本篇文章将主要讲述常用的查询语法。其实MySQL官网给出了多个示例数据库供大家实用查询，下面我们以最常用的员工示例数据库为准，详细介绍各自常用的查询语法。1.员工示例数据库导入官方文档员工示例数据库介绍及下载链接：https://dev.mysql.com/doc/employee/en/employees-installation.h
ESP32-C3入门教程网络篇⑩——基于esp_https_ota和MQTT实现开机主动升级和被动触发升级的OTA功能小康师兄 ESP32-C3入门教程 https 服务器 esp32 OTA MQTT
文章目录一、前言二、软件流程三、部分源码四、运行演示一、前言本文基于VSCodeIDE进行编程、编译、下载、运行等操作基础入门章节请查阅：ESP32-C3入门教程基础篇①——基于VSCode构建HelloWorld教程目录大纲请查阅：ESP32-C3入门教程——导读ESP32-C3入门教程网络篇⑨——基于esp_https_ota实现史上最简单的ESP32OTA远程固件升级功能二、软件流程
2023最详细的Python安装教程（Windows版本）程序员林哥 Python python windows 开发语言
python安装是学习pyhon第一步，很多刚入门小白不清楚如何安装python，今天我来带大家完成python安装与配置，跟着我一步步来，很简单，你肯定能完成。第一部分：python安装（一）准备工作1、下载和安装python(认准官方网站)当然你不想去下载的话也可以分享给你，还有入门学习教程，点击下方卡片跳转进群领取（二）开始安装对于Windows操作系统，可以下载“executableins
【2022 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级 C++语言试题及解析】汉子萌萌哒 CCF noi 算法数据结构 c++
一、单项选择题(共15题，每题2分，共计30分；每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持：()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识，面向对象和类有关，类又涉及父类、子类、继承、派生等关系，printf
ztree设置禁用节点 3213213333332132 JavaScript ztree json setDisabledNode Ajax
ztree设置禁用节点的时候注意，当使用ajax后台请求数据,必须要设置为同步获取数据，否者会获取不到节点对象，导致设置禁用没有效果。 $(function(){ showTree(); setDisabledNode(); });
JVM patch by Taobao bookjovi java HotSpot
在网上无意中看到淘宝提交的hotspot patch，共四个，有意思，记录一下。 7050685：jsdbproc64.sh has a typo in the package name 7058036：FieldsAllocationStyle=2 does not work in 32-bit VM 7060619：C1 should respect inline and
将session存储到数据库中 dcj3sjt126com sql PHP session
CREATE TABLE sessions ( id CHAR(32) NOT NULL, data TEXT, last_accessed TIMESTAMP NOT NULL, PRIMARY KEY (id) ); <?php /** * Created by PhpStorm. * User: michaeldu * Date
Vector 171815164 vector
public Vector<CartProduct> delCart(Vector<CartProduct> cart, String id) { for (int i = 0; i < cart.size(); i++) { if (cart.get(i).getId().equals(id)) { cart.remove(i);
各连接池配置参数比较 g21121 连接池
排版真心费劲，大家凑合看下吧，见谅~ Druid DBCP C3P0 Proxool 数据库用户名称 Username Username User 数据库密码 Password Password Password 驱动名
[简单]mybatis insert语句添加动态字段 53873039oycg mybatis
mysql数据库,id自增,配置如下： <insert id="saveTestTb" useGeneratedKeys="true" keyProperty="id" parameterType=&
struts2拦截器配置云端月影 struts2拦截器
struts2拦截器interceptor的三种配置方法方法1. 普通配置法 <struts> <package name="struts2" extends="struts-default"> &
IE中页面不居中，火狐谷歌等正常 aijuans IE中页面不居中
问题是首页在火狐、谷歌、所有IE中正常显示，列表页的页面在火狐谷歌中正常，在IE6、7、8中都不中，觉得可能那个地方设置的让IE系列都不认识，仔细查看后发现，列表页中没写HTML模板部分没有添加DTD定义，就是<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3
String,int,Integer,char 几个类型常见转换 antonyup_2006 html sql .net
如何将字串 String 转换成整数 int? int i = Integer.valueOf(my_str).intValue(); int i=Integer.parseInt(str); 如何将字串 String 转换成Integer ? Integer integer=Integer.valueOf(str); 如何将整数 int 转换成字串 String ? 1.
PL/SQL的游标类型百合不是茶显示游标(静态游标)隐式游标游标的更新和删除 %rowtype ref游标(动态游标)
游标是oracle中的一个结果集,用于存放查询的结果; PL/SQL中游标的声明; 1,声明游标 2,打开游标(默认是关闭的); 3,提取数据 4,关闭游标注意的要点:游标必须声明在declare中,使用open打开游标,fetch取游标中的数据,close关闭游标隐式游标:主要是对DML数据的操作隐
JUnit4中@AfterClass @BeforeClass @after @before的区别对比 bijian1013 JUnit4 单元测试
一.基础知识 JUnit4使用Java5中的注解（annotation），以下是JUnit4常用的几个annotation： @Before：初始化方法对于每一个测试方法都要执行一次（注意与BeforeClass区别，后者是对于所有方法执行一次）@After：释放资源对于每一个测试方法都要执行一次（注意与AfterClass区别，后者是对于所有方法执行一次
精通Oracle10编程SQL(12)开发包 bijian1013 oracle 数据库 plsql
/* *开发包 *包用于逻辑组合相关的PL/SQL类型（例如TABLE类型和RECORD类型）、PL/SQL项（例如游标和游标变量）和PL/SQL子程序（例如过程和函数） */ --包用于逻辑组合相关的PL/SQL类型、项和子程序，它由包规范和包体两部分组成 --建立包规范：包规范实际是包与应用程序之间的接口，它用于定义包的公用组件，包括常量、变量、游标、过程和函数等 --在包规
【EhCache二】ehcache.xml配置详解 bit1129 ehcache.xml
在ehcache官网上找了多次，终于找到ehcache.xml配置元素和属性的含义说明文档了，这个文档包含在ehcache.xml的注释中！ ehcache.xml ： http://ehcache.org/ehcache.xml ehcache.xsd ： http://ehcache.org/ehcache.xsd ehcache配置文件的根元素是ehcahe ehcac
java.lang.ClassNotFoundException: org.springframework.web.context.ContextLoaderL 白糖_ java eclipse spring tomcat Web
今天学习spring+cxf的时候遇到一个问题：在web.xml中配置了spring的上下文监听器： <listener> <listener-class>org.springframework.web.context.ContextLoaderListener</listener-class> </listener> 随后启动
angular.element boyitech AngularJS AngularJS API angular.element
angular.element 描述: 包裹着一部分DOM element或者是HTML字符串，把它作为一个jQuery元素来处理。（类似于jQuery的选择器啦）如果jQuery被引入了，则angular.element就可以看作是jQuery选择器，选择的对象可以使用jQuery的函数；如果jQuery不可用，angular.e
java-给定两个已排序序列，找出共同的元素。 bylijinnan java
import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class CommonItemInTwoSortedArray { /** * 题目：给定两个已排序序列，找出共同的元素。 * 1.定义两个指针分别指向序列的开始。 * 如果指向的两个元素
sftp 异常，有遇到的吗？求解 Chen.H java jcraft auth jsch jschexception
com.jcraft.jsch.JSchException: Auth cancel at com.jcraft.jsch.Session.connect(Session.java:460) at com.jcraft.jsch.Session.connect(Session.java:154) at cn.vivame.util.ftp.SftpServerAccess.connec
[生物智能与人工智能]神经元中的电化学结构代表什么? comsci 人工智能
我这里做一个大胆的猜想,生物神经网络中的神经元中包含着一些化学和类似电路的结构,这些结构通常用来扮演类似我们在拓扑分析系统中的节点嵌入方程一样,使得我们的神经网络产生智能判断的能力,而这些嵌入到节点中的方程同时也扮演着"经验"的角色.... 我们可以尝试一下...在某些神经
通过LAC和CID获取经纬度信息 dai_lm lac cid
方法1：用浏览器打开http://www.minigps.net/cellsearch.html，然后输入lac和cid信息(mcc和mnc可以填0)，如果数据正确就可以获得相应的经纬度方法2：发送HTTP请求到http://www.open-electronics.org/celltrack/cell.php?hex=0&lac=<lac>&cid=&
JAVA的困难分析 datamachine java
前段时间转了一篇SQL的文章（http://datamachine.iteye.com/blog/1971896），文章不复杂，但思想深刻，就顺便思考了一下java的不足，当砖头丢出来，希望引点和田玉。 -----------------------------------------------------------------------------------------
小学5年级英语单词背诵第二课 dcj3sjt126com english word
money 钱 paper 纸 speak 讲，说 tell 告诉 remember 记得，想起 knock 敲，击，打 question 问题 number 数字，号码 learn 学会，学习 street 街道 carry 搬运，携带 send 发送，邮寄，发射 must 必须 light 灯，光线，轻的 front
linux下面没有tree命令 dcj3sjt126com linux
centos p安装 yum -y install tree mac os安装 brew install tree 首先来看tree的用法 tree 中文解释：tree 功能说明：以树状图列出目录的内容。语　　法：tree [-aACdDfFgilnNpqstux][-I <范本样式>][-P <范本样式
Map迭代方式，Map迭代，Map循环蕃薯耀 Map循环 Map迭代 Map迭代方式
Map迭代方式，Map迭代，Map循环 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年
Spring Cache注解+Redis hanqunfeng spring
Spring3.1 Cache注解依赖jar包：  <dependency> <groupId>org.springframework.data</groupId> <artifactId>spring-data-redis</artifactId>
Guava中针对集合的 filter和过滤功能 jackyrong filter
在guava库中，自带了过滤器(filter)的功能，可以用来对collection 进行过滤，先看例子： @Test public void whenFilterWithIterables_thenFiltered() { List<String> names = Lists.newArrayList("John"
学习编程那点事 lampcy 编程 android PHP html5
一年前的夏天，我还在纠结要不要改行，要不要去学php？能学到真本事吗？改行能成功吗？太多的问题，我终于不顾一切，下定决心，辞去了工作，来到传说中的帝都。老师给的乘车方式还算有效，很顺利的就到了学校，赶巧了，正好学校搬到了新校区。先安顿了下来，过了个轻松的周末，第一次到帝都，逛逛吧！接下来的周一，是我噩梦的开始，学习内容对我这个零基础的人来说，除了勉强完成老师布置的作业外，我已经没有时间和精力去
架构师之流处理---------bytebuffer的mark,limit和flip nannan408 ByteBuffer
1.前言。如题，limit其实就是可以读取的字节长度的意思，flip是清空的意思，mark是标记的意思。 2.例子. 例子代码: String str = "helloWorld"; ByteBuffer buff = ByteBuffer.wrap(str.getBytes()); Sy
org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1, column 1 Everyday都不同 $转义 el表达式
最近在做Highcharts的过程中，在写js时，出现了以下异常：严重: Servlet.service() for servlet jsp threw exception org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1,
用Java实现发送邮件到163 tntxia java实现
/* 在java版经常看到有人问如何用javamail发送邮件？如何接收邮件？如何访问多个文件夹等。问题零散，而历史的回复早已经淹没在问题的海洋之中。本人之前所做过一个java项目，其中包含有WebMail功能，当初为用java实现而对javamail摸索了一段时间，总算有点收获。看到论坛中的经常有此方面的问题，因此把我的一些经验帖出来，希望对大家有些帮助。此篇仅介绍用
探索实体类存在的真正意义 java小叶檀 POJO
一. 实体类简述实体类其实就是俗称的POJO,这种类一般不实现特殊框架下的接口，在程序中仅作为数据容器用来持久化存储数据用的 POJO（Plain Old Java Objects）简单的Java对象它的一般格式就是 public class A{ private String id; public Str

几何入门合集 gym101968 problem F. Mirror + gym102082 Problem F Fair Chocolate-Cutting + gym101915 problem ...

F. Mirror

题意

题解

代码

心路历程

Problem F Fair Chocolate-Cutting

题意

题解

代码

心路历程

B. Ali and Wi-Fi

题意

题解

代码

心路历程

你可能感兴趣的:(几何入门合集 gym101968 problem F. Mirror + gym102082 Problem F Fair Chocolate-Cutting + gym101915 problem ...)