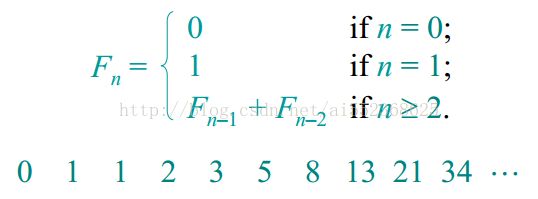MIT算法导论学习笔记-Lecture3：分治法

第三讲 分治法(Devide and Conquer)

思想：大问题分解成小问题，各个击破
步骤：

Step1：Devide——大问题分解成小的问题，e.g.大小为n的问题分解为n/2的问题

Step2：Conquer——(递归地)解决小问题

Step3：Combine——将解合并

e.g. 归并排序

Step1：Devide——将待排序的序列分成两个子序列

Step2：Conquer——(递归地)对每个子序列进行排序

Step3：Combine——将排序好的子序列合并

时间复杂度：

T(n) = 2T(n/2) + Theta(n)

Master Method—>case2，k=0，得到T(n) = Theta(nlgn)

—3.1二分查找(Binary Search)

问题描述：在一个有序序列A中查找元素x

Step1：Devide——将x与序列的中间元素比较

Step2：Conquer——(递归地)在子有序数列中查找x

Step3：Combine——nothing

该问题比较简单，即每次与有序数列的中间的元素比较，如果相等则完成；如果小于该中间的元素，则去较小的一半去查找，如果大于中间的元素则去较大的一半去查找，这样递归地进行，直至找到相等元素。该方法每次查找问题规模减小一半，则很容易得到其时间复杂度。

时间复杂度：

T(n) = T(n/2) + Theta(1)，即T(n) = Theta(lgn)

一个简单的代码实现：

非递归版本

// binary search, if so return the position,else return -1
// Non-Recursive version.
int BinarySearch(int *Array,int x,int L) //L is the length of the sorted array
{
	int low, mid, high ;
	low = 0 ;
	
	high = L - 1 ;
	//mid = (low + high + 1)/2 ;
	while (low < high)
	{

		mid = (high + low + 1)/2 ;//the index is not right
		if (Array[mid] == x)
		{
			return mid ;
		}
		else if (Array[mid] < x)
		{
			low = mid + 1;
			
		}
		else
		{
			high = mid - 1;
			//mid = (high + low + 1)/2 ;
		}
	}
	return -1;
}

递归版本：

// binary search, if so return the position,else return -1
// Recursive version.
int BinarySearchRecursive(int *Array,int x,int Low,int High) //L is the length of the sorted array
{
	int mid;
	mid = (Low + High + 1)/2 ;

	if (Low < High)
	{
		if (Array[mid] < x)
		{
			Low = mid + 1 ;
			return BinarySearchRecursive(Array,x,Low,High) ;
		}
		else if (Array[mid] > x)
		{
			High = mid - 1;
			return BinarySearchRecursive(Array,x,Low,High) ;
		}
		else
			return mid ;
	}
	else
		return -1 ;
}

虽然该算法是一个递归运算,但显然非递归方法更容易理解.

本文给出了二分查找的简单实现,程序参照了如下博客:

http://blog.csdn.net/yangtrees/article/details/8898997

关于二分查找更详尽的讨论,可以参照如下博客:

http://www.cppblog.com/converse/archive/2009/10/05/97905.html

—3.2幂次方问题 (Powering a Num)

         问题描述:给定一个数x(int/float)，和一个正整数n，求x^n

         3.2.1 基本实现方法

即，将x相乘n-1次，代码为：

DataType PoweringNum(DataType x, int n)
{
	DataType ans = x;
	for (int i = 1; i < n; i ++)
	{
		ans *= x ;
	}
	return ans ;
}

该方法的时间复杂度为：T(n) = Theta(n)，即线性的。

3.2.2 二分法：

实现方法如下图：

时间复杂度：

                   T(n)= T(n/2) + Theta(1)，即T(n) = Theta(lgn)

该算法的一个简单代码实现为：

DataType PoweringNumRecursive(DataType x, int n)
{
	DataType ans = 0 ;
	if ( n > 1 && 0 == n%2) // n is an even num
	{
		n /= 2 ;
		ans = PoweringNumRecursive(x,n) ;
		return ans*ans ;
	}
	else if(n > 1)
	{
		n /= 2 ;
		ans = PoweringNumRecursive(x,n) ;
		return ans*ans*x ;
	}
	else
	{
		return x ;
	}
}

—3.3斐波那契数列(Fibonacci Num)

问题描述：

3.3.1 基本方法——递归法

该方法要计算Fn，则计算Fn-1和Fn-2，etc。该方法的时间复杂度为：T(n) = Omega(q^n),q = (1 + sqrt(5))/2,即黄金分割点，即该方法是指数级的时间复杂度。

简单代码：

//Fibonacci num
int FibonacciNum(int n)
{
	if(n >= 2)
	{
		return FibonacciNum(n-1) + FibonacciNum(n-2) ;
	}
	else 
	{
		return n ;
	}
}

3.3.2 Bottom-Up法(从头到尾)

思想：按顺序计算Fn，则每个Fn只需要计算一次，下一次可以用上一次的计算结果，这样改进后算法的时间复杂度就降低为线性时间复杂度，即T(n) = Theta(n)

简单代码：

int FibonacciNum_BottomUp(int n)
{
	int ans ;
	if (n < 2)
	{
		ans = n ;
	}
	else
	{
		int a0 = 0, a1 = 1 ;
		int i = 2 ;
		while (i <= n)
		{
			ans = a0 + a1 ;
			a0 = a1 ;
			a1 = ans ;
			i ++ ;
		}
	}
	return ans ;
}

3.3.3 平方递归法

1). 朴素平方递归法

        该方法用到Fibonacci数列的一个性质，即

         Fn= [q^n/sqrt(5)]，q为上面提到的黄金分割点，[a]表示离a最近的整数。

该方法的时间复杂度与上面求幂次方的时间复杂度相同，即T(n) = Theta(lgn)

该方法理论上是可行的，但是实际应用时却会遇到问题，即浮点运算容易出现舍入误差，而且据我所知，C语言中没有专门的取最近整数的函数。

 2).平方递归法

         该方法用到Fibonacci数列的另一个性质，即：

该性质在理论上和实际上都是可行的，其时间复杂度为：T(n) = Theta(lgn)

int *MatrixMulMatrix_2x2(int const a[4],int const b[4])//row major store
{
	int *c ;
	c = (int *)malloc(4*sizeof(int)) ;
	c[0] = a[0]*b[0] + a[1]*b[2] ;
	c[1] = a[0]*b[1] + a[1]*b[3] ;
	c[2] = a[2]*b[0] + a[3]*b[2] ;
	c[3] = a[2]*b[1] + a[3]*b[3] ;
	return c ;
}
int *FibonacciNum_PowerRecursive(int n,int input[4])
{
	int *output ;
	output = (int *)malloc(4*sizeof(int)) ;
	int *output1 ;
	output1 = (int *)malloc(4*sizeof(int)) ;
	if ( n > 1 && 0 == n%2) // n is an even num
	{
		n /= 2 ;
		output1 = FibonacciNum_PowerRecursive(n,input) ;
		output = MatrixMulMatrix_2x2(output1,output1) ;
		return output ;
	}
	else if(n > 1)
	{
		n /= 2 ;
		output1 = FibonacciNum_PowerRecursive(n,input) ;
		// Repeated use of output1 and output.
		output = MatrixMulMatrix_2x2(output1,output1) ;
		output1 = MatrixMulMatrix_2x2(output,input) ;
		return output1 ;
	}
	else if(1 == n)
	{
		return input ; 
	}
	// Take n = 0 into consideration.
	else 
	{
		input[1] = 0 ;
		input[2] = 0 ;
		return input ;
	}
}

注意：上面实现中，2x2矩阵用一个一位数组按行优先来存储，这样Fn即为输出一位数组的output[1]或者output[2]；另一个需要注意的是，该方法不适用于n=0的情况，由上图定义很好理解，n=0时Fn-1无意义，但是由于我们只关心的是output[1]或者output[2]的正确与否，所以程序实现时在最后一个else里面考虑了该种情况，即通过将input对应的值改变包括该情况。

—3.4 矩阵乘法(只考虑方阵)

矩阵乘法是一个相对来说比较困难的问题，所需篇幅较大；而且Strassen矩阵相乘这种经典算法，值得专门写一篇来讨论，所以矩阵相乘将放在下一篇来讨论。

—3.5 分治法解决VLSI layout(VeryLarge Scale Integration,超大规模集成电路布局问题)

问题描述：怎样将一个n个叶子的完全二叉树布局，使得所占用面积最小？

想了好久，加不加入这一小节，还是加上吧。原因有二：一这样可以与视频匹配；二这种分治法用到VLSI中，为什么最开始不是我们想到的呢？这种创新性是怎么来的呢？由此可以看到国外的在这种发散思维上还是比我们要做的好。

3.5.1 基本实现方法

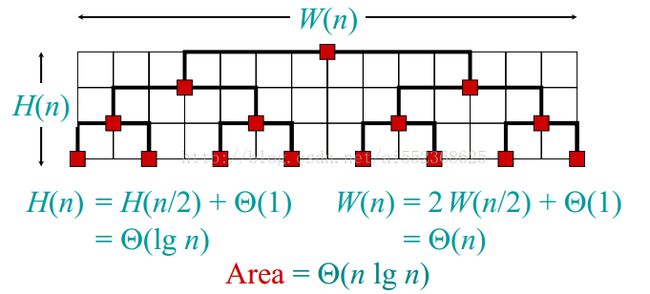
上图可以说是一个最naïve的想法，则n个叶子的完全二叉树，其占的高度为H(n) = Theta(lgn)，占用的宽度为W(n) = Theta(n),占用面积为Area = Theta(nlgn).

怎么样使其变成线性复杂度呢？？？

3.5.2 H布线法

对其分析，从图上一眼就能看明白。然而，最重要的不是这个想法有多巧妙，而是分治法的思想是怎样运用的。

要想得到一个线性复杂度的面积，则需要长宽(假设为矩形)的复杂度之乘积为线性的，那么最基本的想法是：

W(n) = H(n) = Theta(sqrt(n))

有了这个目标函数(也可以说Area =Theta(n)为目标函数)，怎么计算呢？？这便用到了上一讲的 Master Method，即

 T(n)= aT(n/2a) + O(n^(1/2-e))

式中，e为一个小的数，第二项表示的意思是时间复杂度小于n^(1/2)

根据Master Method，case1，上式的时间复杂度显然为Theta(n)

那么，最简单的a=2，这便得到了上图中的方法，当然由该公式得到上面布线的idea还需要经验等等，但是这种由目标函数来反推解决方法总比盲目地尝试要来得快得多。

由此可见，这种看似简单的分治法，真正达到了融会贯通也将大有用处的。