序列比对(一)——全局比对Needleman-Wunsch算法
原创:hxj7
前言
序列比对是生信领域的一个古老课题,在这一波NGS的浪潮中重新引起大家的广泛关注。由于生物序列的特殊性,在比对的时候允许插入缺失,所以往往是一种不精确匹配。从本文开始,我们陆续学习前人开发出的流行算法。
全局比对算法
所谓全局比对算法,就是根据一个打分矩阵(替换矩阵)计算出两个序列比对最高得分的算法。关于它的介绍网上已经非常多了,我们只需看看其中的关键点及实现代码。
关键点
1. 打分矩阵:
选用不同的打分矩阵或者罚分分值会导致比对结果不同,常用BLAST打分矩阵。
2. 计算比对最高得分的算法:
常用动态规划算法(Needleman-Wunsch算法)。
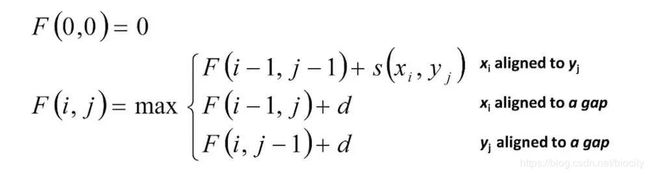
图片引自https://www.jianshu.com/p/2b99d0d224a2
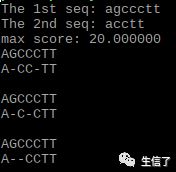
3. 打印出最高得分相应的序列比对结果:
根据得分矩阵回溯,如果最优比对结果有多个,全部打印出来。
4. 理解打分系统背后的概率论模型:
比对分值可以理解为匹配模型和随机模型的对数几率比(log-odds ratio)。
实现代码(C代码及示例)
网上的教程给出的代码大多不全,所以我决定还是自己造轮子了。
需要说明的是:
1. 没有对输入进行检查,如果有非AGCT的字符程序可能会出错。
2. 对空位的罚分是线性的,即penalty=g*d,其中g为空位长度,d为一个空位的罚分。
在以后的文章中,我们会给出仿射型罚分的代码,即
penalty=d+(g-1)*e,其中g为连续空位的长度,d为连续空位中第一个空位的罚分,e为连续空位中第2个及以后空位的罚分。
3. 其他未提及的错误或者不足。
#include (公众号:生信了)