Kmeans算法 动画演示
1. 概述
K-means聚类算法也称k均值聚类算法,是集简单和经典于一身的基于距离的聚类算法。它采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为类簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
2. 算法核心思想
K-means聚类算法是一种迭代求解的聚类分析算法,其步骤是随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。
3. 算法实现步骤
1、首先确定一个k值,即我们希望将数据集经过聚类得到k个集合。
2、从数据集中随机选择k个数据点作为质心。
3、对数据集中每一个点,计算其与每一个质心的距离(如欧式距离),离哪个质心近,就划分到那个质心所属的集合。
4、把所有数据归好集合后,一共有k个集合。然后重新计算每个集合的质心。
5、如果新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),我们可以认为聚类已经达到期望的结果,算法终止。
6、如果新质心和原质心距离变化很大,需要迭代3~5步骤。
4. 算法步骤图解
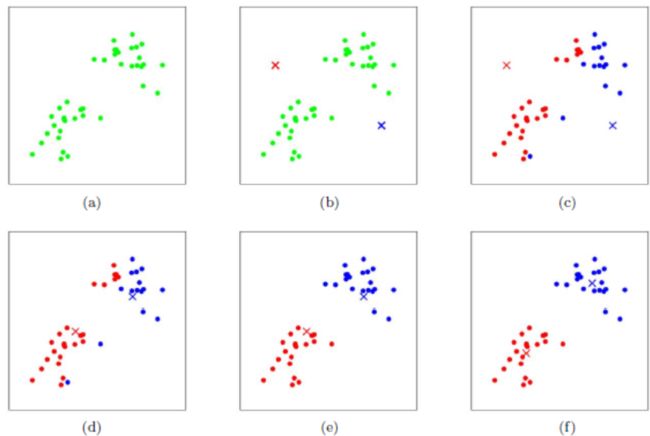
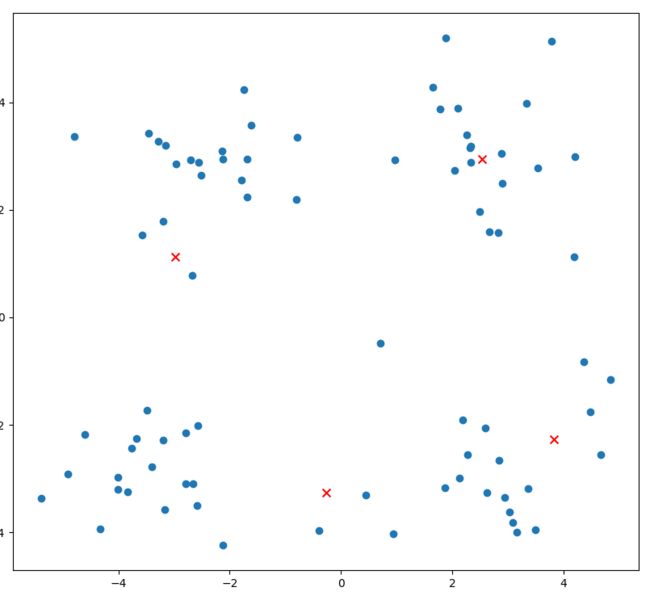
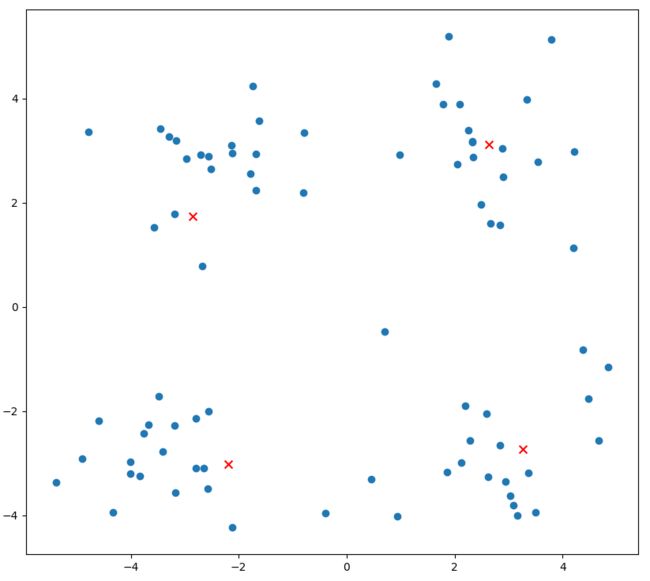
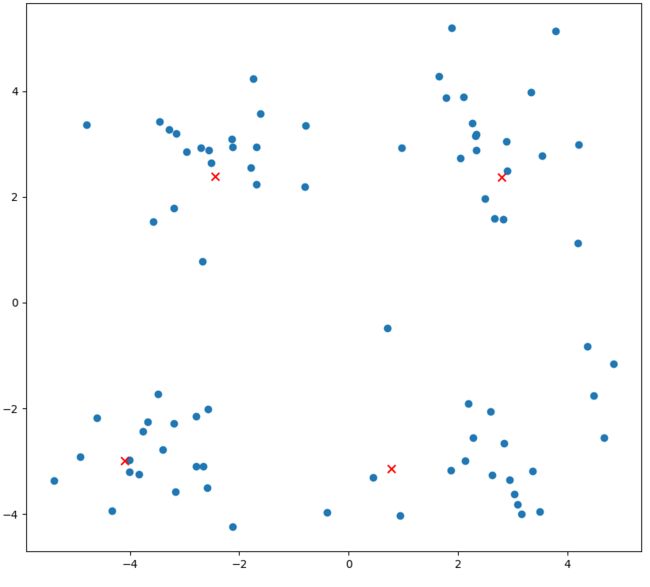
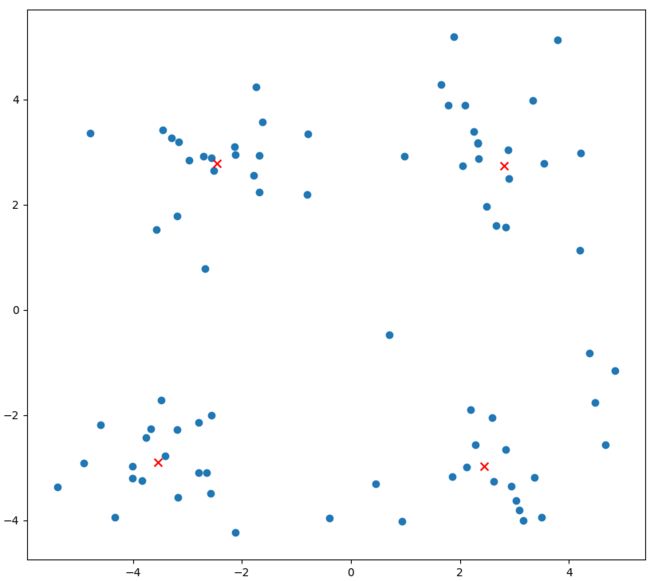
上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图d所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。
上图a表达了初始的数据集,假设k=4时,图中质心的变化。
K-means术语:
簇:所有数据的点集合,簇中的对象是相似的。
质心:簇中所有点的中心(计算所有点的中心而来)
5. K-means算法优缺点
优点:
1、原理比较简单,实现也是很容易,收敛速度快。
2、当结果簇是密集的,而簇与簇之间区别明显时, 它的效果较好。
3、主要需要调参的参数仅仅是簇数k。
缺点:
1、K值需要预先给定,很多情况下K值的估计是非常困难的。
2、K-Means算法对初始选取的质心点是敏感的,不同的随机种子点得到的聚类结果完全不同 ,对结果影响很大。
3、对噪音和异常点比较的敏感。用来检测异常值。
4、采用迭代方法,可能只能得到局部的最优解,而无法得到全局的最优解。
6. 算法实现
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time : 2020.03.18
# Author : cehkongfu
# File : kmeans.py
# Software: eclipse
#from : https://www.cnblogs.com/ahu-lichang/p/7161613.html
import sys
#reload(sys)
#sys.setdefaultencoding('UTF-8')
from numpy import *
import matplotlib.pyplot as plt
# 加载数据
def loadDataSet(fileName): # 解析文件,按tab分割字段,得到一个浮点数字类型的矩阵
dataMat = [] # 文件的最后一个字段是类别标签
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = list(map(float, curLine)) # 将每个元素转成float类型
dataMat.append(fltLine)
return dataMat
# 计算欧几里得距离
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离
# 构建聚簇中心,取k个(此例中k=4)随机质心
def randCent(dataSet, k):
n = shape(dataSet)[1]
centroids = mat(zeros((k,n))) # 每个质心有n个坐标值,总共要k个质心
for j in range(n):
minJ = min(dataSet[:,j])
maxJ = max(dataSet[:,j])
rangeJ = float(maxJ - minJ)
centroids[:,j] = minJ + rangeJ * random.rand(k, 1)
return centroids
# k-means 聚类算法
def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
'''
:param dataSet: 没有lable的数据集 (本例中是二维数据)
:param k: 分为几个簇
:param distMeans: 计算距离的函数
:param createCent: 获取k个随机质心的函数
:return: centroids: 最终确定的 k个 质心
clusterAssment: 该样本属于哪类 及 到该类质心距离
'''
colors=['r', 'g', 'b', 'k']
m = shape(dataSet)[0] #m=80,样本数量
clusterAssment = mat(zeros((m,2)))
# clusterAssment第一列存放该数据所属的中心点,第二列是该数据到中心点的距离,
centroids = createCent(dataSet, k)
clusterChanged = True # 用来判断聚类是否已经收敛
x=array(datMat[:,0]).ravel()
y=array(datMat[:,1]).ravel()
plt.figure(figsize=(10,9))
while clusterChanged:
clusterChanged = False;
for i in range(m): # 把每一个数据点划分到离它最近的中心点
minDist = inf; minIndex = -1;
for j in range(k):
distJI = distMeans(centroids[j,:], dataSet[i,:])
if distJI < minDist:
minDist = distJI; minIndex = j # 如果第i个数据点到第j个中心点更近,则将i归属为j
if clusterAssment[i,0] != minIndex:
clusterChanged = True # 如果分配发生变化,则需要继续迭代
clusterAssment[i,:] = minIndex,minDist**2 # 并将第i个数据点的分配情况存入字典
#画图
# print centroids
for cent in range(k): # 重新计算中心点
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 去第一列等于cent的所有列
centroids[cent,:] = mean(ptsInClust, axis = 0) # 算出这些数据的中心点
plt.cla()
plt.scatter(x,y, marker='o')
xcent=array(centroids[:,0]).ravel()
ycent=array(centroids[:,1]).ravel()
plt.scatter( xcent, ycent, marker='x', color='r', s=50)
plt.pause(2)
return centroids, clusterAssment
# --------------------测试----------------------------------------------------
# 用测试数据及测试kmeans算法
if __name__ == '__main__':
datMat = mat(loadDataSet('test.txt'))
kMeans(datMat, 4)
数据集【test.txt】
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
2.668759 1.594842
-3.156485 3.191137
3.165506 -3.999838
-2.786837 -3.099354
4.208187 2.984927
-2.123337 2.943366
0.704199 -0.479481
-0.392370 -3.963704
2.831667 1.574018
-0.790153 3.343144
2.943496 -3.357075
-3.195883 -2.283926
2.336445 2.875106
-1.786345 2.554248
2.190101 -1.906020
-3.403367 -2.778288
1.778124 3.880832
-1.688346 2.230267
2.592976 -2.054368
-4.007257 -3.207066
2.257734 3.387564
-2.679011 0.785119
0.939512 -4.023563
-3.674424 -2.261084
2.046259 2.735279
-3.189470 1.780269
4.372646 -0.822248
-2.579316 -3.497576
1.889034 5.190400
-0.798747 2.185588
2.836520 -2.658556
-3.837877 -3.253815
2.096701 3.886007
-2.709034 2.923887
3.367037 -3.184789
-2.121479 -4.232586
2.329546 3.179764
-3.284816 3.273099
3.091414 -3.815232
-3.762093 -2.432191
3.542056 2.778832
-1.736822 4.241041
2.127073 -2.983680
-4.323818 -3.938116
3.792121 5.135768
-4.786473 3.358547
2.624081 -3.260715
-4.009299 -2.978115
2.493525 1.963710
-2.513661 2.642162
1.864375 -3.176309
-3.171184 -3.572452
2.894220 2.489128
-2.562539 2.884438
3.491078 -3.947487
-2.565729 -2.012114
3.332948 3.983102
-1.616805 3.573188
2.280615 -2.559444
-2.651229 -3.103198
2.321395 3.154987
-1.685703 2.939697
3.031012 -3.620252
-4.599622 -2.185829
4.196223 1.126677
-2.133863 3.093686
4.668892 -2.562705
-2.793241 -2.149706
2.884105 3.043438
-2.967647 2.848696
4.479332 -1.764772
-4.905566 -2.911070
运算结果