高斯消去法SSE并行化实验
高斯消去法原理和伪代码:
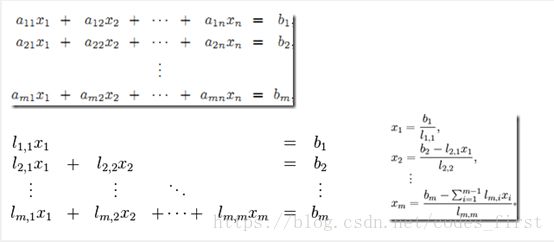
高斯消去法(LU分解),是线性代数中的一个算法,可用来求解线性方程组,并可以求出矩阵的秩,以及求出可逆方阵的逆矩阵。高斯消元法的原理是:若用初等行变换将增广矩阵化为 ,则AX = B与CX = D是同解方程组。所以我们可以用初等行变换把增广矩阵转换为行阶梯阵,然后回代求出方程的解。
总结一套流程就是:
原线性方程组——> 高斯消元法——> 下三角或上三角形式的线性方程组——>前向替换算法求解(对于上三角形式,采用后向替换算法)
所以高斯消去法(LU分解)串行算法如下面伪代码所示:
for k := 1 to n do
for j := k to ndo
A[k, j] := A[k, j]/A[k, k];
for i := k + 1to n do
for j := k + 1 to n do
A[i, j] := A[i, j] - A[i, k] × A[k, j ];
A[i, k] := 0;这其中,内嵌的第一个for循环的作用是把第k行的所有元素除以第一个非零元素,目的是第一个非零元为1
而第二个内嵌的for循环(当然其中还内嵌了一个小的for循环)作用是从k+1行开始减去第k行乘以这一行行的第一个非零元,使得k+1行的第k列为0
SSE/AVX介绍:
Intel ICC和开源的GCC编译器支持的SSE/AVX指令的C接口声明在xmmintrin.h和pmmintrin.h头文件中。其数据类型命名主要有__m128/__m256、__m128d/__m256i,默认为单精度(d表示双精度,i表示整型)。其函数的命名可大致分为3个使用“_”隔开的部分,3个部分的含义如下。
第一个部分为_mm或_mm256。_mm表示其为SSE指令,操作的向量长度为64位或128位。_mm256表示AVX指令,操作的向量长度为256位。本节只介绍128位的SSE指令和256位的AVX指令。
第二个部分为操作函数名称,如_add、_load、mul等,一些函数操作会增加修饰符,如loadu表示不对齐到向量长度的存储器访问。
第三个部分为操作的对象名及数据类型,_ps表示操作向量中所有的单精度数据;_pd表示操作向量中所有的双精度数据;_pixx表示操作向量中所有的xx位的有符号整型数据,向量寄存器长度为64位;_epixx表示操作向量中所有的xx位的有符号整型数据,向量寄存器长度为128位;_epuxx表示操作向量中所有的xx位的无符号整型数据,向量寄存器长度为128位;_ss表示只操作向量中第一个单精度数据;si128表示操作向量寄存器中的第一个128位有符号整型。
3个部分组合起来,就形成了一条向量函数,如_mm256_add_ps表示使用256位向量寄存器执行单精度浮点加法运算。由于使用指令级数据并行,因此其粒度非常小,需要使用细粒度的并行算法设计。SSE/AVX指令集对分支的处理能力非常差,而从向量中抽取某些元素数据的代价又非常大,因此不适合含有复杂逻辑的运算。
现在对于接下来代码中要用到的几个SSE指令加以介绍:
_mm_loadu_ps用于packed的加载(下面的都是用于packed的),不要求地址是16字节对齐,对应指令为movups。
_mm_sub_ps(__m128_A,__m128_B);返回一个__m128的寄存器,仅将寄存器_A和寄存器_B最低对应位置的32bit单精度浮点数相乘,其余位置取寄存器_A中的数据,例如_A=(_A0,_A1,_A2,_A3),_B=(_B0,_B1,_B2,_B3),则返回寄存器为r=(_A0*_B0,_A1,_A2,_A3)
_mm_storeu_ps(float *_V, __m128 _A);返回一个__m128的寄存器,Sets the low word to the single-precision,floating-pointValue of b,The upper 3 single-precision,floating-pointvalues are passed throughfrom a,r0=_B0,r1=_A1,r2=_A2,r3=_A3
SSE算法设计与实现:
通过分析高斯的程序可以发现,高斯消去法有两部分可以实现并行,分别是第一部分的除法和第二部分的减法。即:
1.第一个内嵌的for循环里的A[k, j]:= A[k, j]/A[k, k]; 我们可以做除法并行
2.第二个双层for循环里的A[i, j] := A[i, j] - A[i, k] × A[k, j ];我们可以做减法并行
我们来看核心代码
1. 首先没加上并行化的高斯消去法:
float** normal_gaosi(float **matrix) //没加SSE串行的高斯消去法
{
for (int k = 0; k < N; k++)
{
float tmp =matrix[k][k];
for (int j = k; j < N; j++)
{
matrix[k][j] = matrix[k][j] / tmp;
}
for (int i = k + 1; i < N; i++)
{
float tmp2 = matrix[i][k];
for (int j = k + 1; j < N; j++)
{
matrix[i][j] = matrix[i][j] - tmp2 * matrix[k][j];
}
matrix[i][k] = 0;
}
}
return matrix;
}2. 再来看加上并行化的高斯消去法:
void SSE_gaosi(float **matrix) //加了SSE并行的高斯消去法
{
__m128 t1, t2, t3, t4;
for (int k = 0; k < N; k++)
{
float tmp[4] = { matrix[k][k], matrix[k][k], matrix[k][k], matrix[k][k] };
t1 = _mm_loadu_ps(tmp);
for (int j = N - 4; j >=k; j -= 4) //从后向前每次取四个
{
t2 = _mm_loadu_ps(matrix[k] + j);
t3 = _mm_div_ps(t2, t1);//除法
_mm_storeu_ps(matrix[k] + j, t3);
}
if (k % 4 != (N % 4)) //处理不能被4整除的元素
{
for (int j = k; j % 4 != ( N% 4); j++)
{
matrix[k][j] = matrix[k][j] / tmp[0];
}
}
for (int j = (N % 4) - 1; j>= 0; j--)
{
matrix[k][j] = matrix[k][j] / tmp[0];
}
for (int i = k + 1; i < N; i++)
{
float tmp[4] = { matrix[i][k], matrix[i][k], matrix[i][k], matrix[i][k] };
t1 = _mm_loadu_ps(tmp);
for (int j = N - 4; j >k;j -= 4)
{
t2 = _mm_loadu_ps(matrix[i] + j);
t3 = _mm_loadu_ps(matrix[k] + j);
t4 = _mm_sub_ps(t2,_mm_mul_ps(t1, t3)); //减法
_mm_storeu_ps(matrix[i] + j, t4);
}
for (int j = k + 1; j % 4 !=(N % 4); j++)
{
matrix[i][j] = matrix[i][j] - matrix[i][k] * matrix[k][j];
}
matrix[i][k] = 0;
}
}
}
实验结果分析:
为了测试其性能,我们把矩阵的大小从8,64,512,1024,2048,4096的矩阵进行高斯消去,并将串行所花费的时间与并行所花费的时间进行对比。因为后边矩阵太大我们仅看时间对比即可
1. N=8时,由于数据量较小,所花时间差距并不大。
2. N=64,由于数据量较小,所花时间差距并不大。
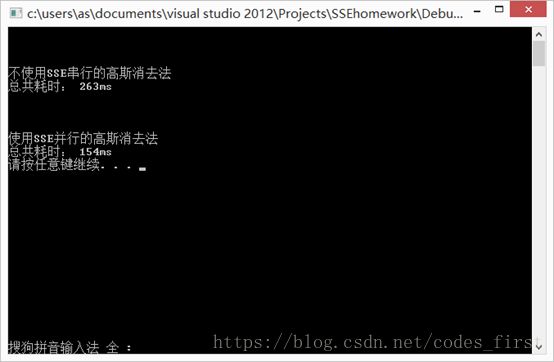
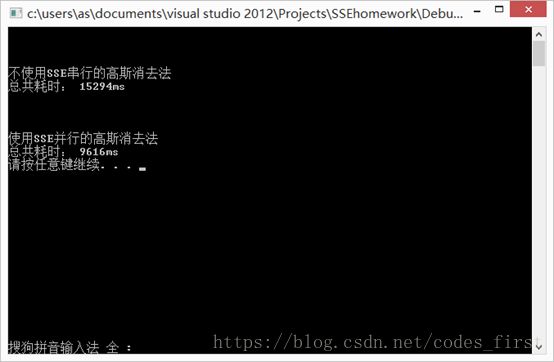
3. N=512,这里开始我们看到时间上的变化了。之后随着数据量逐渐增加,并行的优势逐渐体现出来。
4. N=1024
5. N=2048
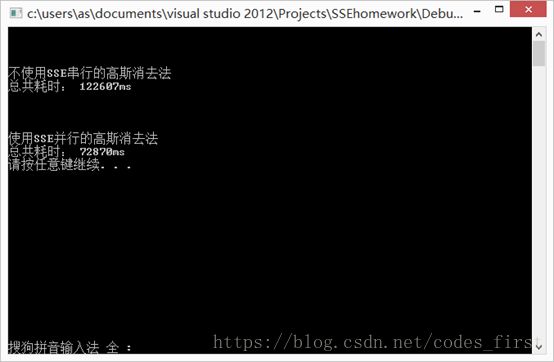
6. N=4096
总的来说,优势并没有特别大,究其原因,我觉得是因为在做最后并行的步骤之前有很多固定的步骤是需要一定时间的,比如对齐,导致SSE并行的方法需要花时间代价在这上面,没有想象中得那么快。
附上整个代码:
#include
#include
#include
#include
#defineN 4096
usingnamespace std;
float** normal_gaosi(float **matrix) //没加SSE串行的高斯消去法
{
for (int k = 0; k < N; k++)
{
float tmp =matrix[k][k];
for (int j = k; j < N; j++)
{
matrix[k][j] = matrix[k][j] / tmp;
}
for (int i = k + 1; i < N; i++)
{
float tmp2 = matrix[i][k];
for (int j = k + 1; j < N; j++)
{
matrix[i][j] = matrix[i][j] - tmp2 * matrix[k][j];
}
matrix[i][k] = 0;
}
}
returnmatrix;
}
void SSE_gaosi(float **matrix) //加了SSE并行的高斯消去法
{
__m128 t1, t2, t3, t4;
for (int k = 0; k < N; k++)
{
float tmp[4] = { matrix[k][k], matrix[k][k], matrix[k][k], matrix[k][k] };
t1 = _mm_loadu_ps(tmp);
for (int j = N - 4; j >=k; j -= 4) //从后向前每次取四个
{
t2 = _mm_loadu_ps(matrix[k] + j);
t3 = _mm_div_ps(t2, t1);//除法
_mm_storeu_ps(matrix[k] + j, t3);
}
if (k % 4 != (N % 4)) //处理不能被4整除的元素
{
for (int j = k; j % 4 != ( N% 4); j++)
{
matrix[k][j] = matrix[k][j] / tmp[0];
}
}
for (int j = (N % 4) - 1; j>= 0; j--)
{
matrix[k][j] = matrix[k][j] / tmp[0];
}
for (int i = k + 1; i < N; i++)
{
float tmp[4] = { matrix[i][k], matrix[i][k], matrix[i][k], matrix[i][k] };
t1 = _mm_loadu_ps(tmp);
for (int j = N - 4; j >k;j -= 4)
{
t2 = _mm_loadu_ps(matrix[i] + j);
t3 = _mm_loadu_ps(matrix[k] + j);
t4 = _mm_sub_ps(t2,_mm_mul_ps(t1, t3)); //减法
_mm_storeu_ps(matrix[i] + j, t4);
}
for (int j = k + 1; j % 4 !=(N % 4); j++)
{
matrix[i][j] = matrix[i][j] - matrix[i][k] * matrix[k][j];
}
matrix[i][k] = 0;
}
}
}
void print(float **matrix) //输出
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cout << matrix[i][j]<<" ";
}
cout << endl;
}
}
int main()
{
srand((unsigned)time(NULL));
float **matrix = newfloat*[N];
float **matrix2 = newfloat*[N];
for (int i = 0; i