2018年计蒜客蓝桥杯模拟赛(2018.3.25)题解(未完待续)
(题解参考:2018年蓝桥杯模拟赛第五场题解 by islands)
一、题目列表
1. (3')矩阵求和
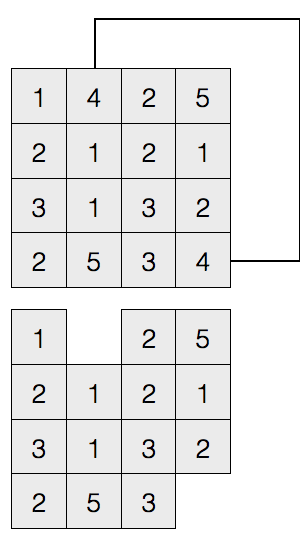
给你一个n×n的矩阵,里面填充1到n×n。例如当n等于3的时候,填充的矩阵如下。
1 2 3
4 5 6
7 8 9
现在我们把矩阵中的每条边的中点连起来,这样形成了一个新的矩形,请你计算一下这个新的矩形的覆盖的数字的和。比如,n=3的时候矩形覆盖的数字如下。
2
4 5 6
8
那么当 n 等于 101 的时候,矩阵和是多少?
2. (9')素数个数
用 0,1,2,3, ... , 7 这8个数组成的所有整数中,质数有多少个(每个数字必须用到且只能用一次)。
提示:以 0 开始的数字是非法数字。
3. (11')连连看
连连看是一款非常有意思的游戏。
我们可以把任意两个在图的在边界上的相同的方格一起消掉,比如把两个 4 消掉以后,
每次消掉两个方格的时候,都有会获得一个分数,第 i 次消的分数为 i×方格的值 。比如上面的消法,是第一次消,获得的分数为1×4=4。请你帮忙计算最优操作情况下,获得的分数最多为多少。
4. (7')快速幂
一个数的整数次幂,是我们在计算中经常用到的,但是怎么可以在 O(log(n)) 的时间内算出结果呢?
代码框中的代码是一种实现,请分析并填写缺失的代码,求 x^y mod p 的结果。
#include
int pw(int x, int y, int p) {
if (!y) {
return 1;
}
int res = /*在这里填写必要的代码*/;
if (y & 1) {
res = res * x % p;
}
return res;
}
int main() {
int x, y, p;
scanf("%d%d%d", &x, &y, &p);
printf("%d\n", pw(x, y, p));
return 0;
}
5. (13')末尾零的个数
N! 末尾有多少个 0 呢? N!=1×2×⋯×N。
代码框中的代码是一种实现,请分析并填写缺失的代码。
#include
int main() {
int n, ans = 0;
scanf("%d", &n);
while (n) {
ans += /*在这里填写必要的代码*/;
}
printf("%d\n", ans);
return 0;
}
6. (16')藏宝图
蒜头君得到一张藏宝图。藏宝图是一个 10×10 的方格地图,图上一共有 10 个宝藏。有些方格地形太凶险,不能进入。
整个图只有一个地方可以出入,即是入口也是出口。蒜头君是一个贪心的人,他规划要获得所有宝藏以后才从出口离开。
藏宝图上从一个方格到相邻的上下左右的方格需要 1 天的时间,蒜头君从入口出发,找到所有宝藏以后,回到出口,最少需要多少天。
7. (15')合并数字
蒜头君得到了 n 个数,他想对这些数进行下面这样的操作,选出最左边的相邻的差的绝对值为 1 的两个数,只保留较小的数,删去较大的数,直到没有两个相邻的差的绝对值为 1 的数,问最多可以进行多少次这样的操作?
输入格式
输入第一行为一个整数 n(1 <=n<= 10^5),表示数字的总数
第二行为 n 个整数 x1,x2,...,xn (0≤xi≤10^9),表示这些数。
输出格式
输出一行,为一个整数,表示蒜头君最多可以进行多少次这样的操作。
样例输入
4 1 2 0 1
样例输出
3
8. (20')蒜头君下棋
蒜头君喜欢下棋。最近它迷上了国际象棋。国际象棋的棋盘可以被当做一个 8\times 88×8 的矩阵,棋子被放在格子里面(不是和中国象棋一样放在线上)。
蒜头君特别喜欢国际象棋里面的马,马的移动规则是这样的:横着走两步之后竖着走一步,或者横着走一步之后竖着走两步。例如,一匹马在 (3,3) 的位置,则它可以到达的地方有 (1,2),(2,1),(1,4),(4,1),(5,2),(2,5),(5,4),(4,5)八个地方。蒜头君想要把整个棋盘都放上马,并且让这些马不能相互攻击(即任何一匹马不能走一步之后就到达另一匹马的位置)。蒜头君当然知道在 8×8 的棋盘上怎么放马,但如果棋盘变为 n×m 的,蒜头君就不懂了。他希望你来帮忙他计算一下究竟能放多少匹马。
输入格式
共一行,两个整数n和m (1≤n,m≤1000),代表棋盘一共有 n 行 m列。
输出格式
输出一个整数,代表棋盘上最多能放的马的数量。
样例输入1
2 4
样例输出1
4
样例输入2
3 4
样例输出2
6
9. (25')蒜头君的数轴
今天蒜头君拿到了一个数轴,上边有 n 个点,但是蒜头君嫌这根数轴不够优美,想要通过加一些点让它变优美,所谓优美是指考虑相邻两个点的距离,最多只有一对点的距离与其它的不同。
蒜头君想知道,他最少需要加多少个点使这个数轴变优美。
输入格式
输入第一行为一个整数 n(1 <=n<= 10^5),表示数轴上的点数。
第二行为 n个不重复的整数 x1,x2,...,xn(−10^9≤xi≤10^9),表示这些点的坐标,点坐标乱序排列。
输出格式
输出一行,为一个整数,表示蒜头君最少需要加多少个点使这个数轴变优美。
样例输入
4 1 3 7 15
样例输出
1
10. (31')划分整数
蒜头君特别喜欢数学。今天,蒜头君突发奇想:如果想要把一个正整数 n分解成不多于 k个正整数相加的形式,那么一共有多少种分解的方式呢?
蒜头君觉得这个问题实在是太难了,于是他想让你帮帮忙。
输入格式
共一行,包含两个整数 n(1≤n≤300) 和 k(1≤k≤300),含义如题意所示。
输出格式
一个数字,代表所求的方案数。
样例输入
5 3
样例输出
5
==================================================================
二、解答
1. 【分析】找规律
法一:根据题意,我们可按行序对矩阵填充 1~n*n 这n*n个数(当然这里n必为奇数),然后找到矩阵4条边的中点(中点横/纵坐标值为n/2+1),连成一个矩形。在该矩形边上以及内部的数是我们要进行求和的。
#include
#define maxn 105
int mat[maxn][maxn];
int main()
{
int i,j;
int k=0,mid=51;
int num=1,sum=0;
for(i=1;i<=101;i++)
for(j=1;j<=101;j++)
mat[i][j]=num++;
for(i=1;i<=mid;i++)
{
for(j=mid-k;j<=mid+k;j++)
{
printf("%d ",mat[i][j]);
sum+=mat[i][j];
}
k++;
printf("\n");
}
k-=2;
for(i=mid+1;i<=101;i++)
{
for(j=mid-k;j<=mid+k;j++)
{
printf("%d ",mat[i][j]);
sum+=mat[i][j];
}
k--;
printf("\n");
}
printf("%d\n",sum);
return 0;
} 法二:考虑所有需要计算的点到中心点的距离(横坐标加纵坐标的距离和),它们都是小于等于 n / 2 的。因此只需把满足条件的点加上即可。
#include
#include
int main()
{
int i,j;
int sum=0,cnt=0; //sum-所求矩形元素和 cnt-(i,j)位置对应的元素
for(i=0;i<101;i++)
{
for(j=0;j<101;j++)
{
cnt++;
if(fabs(101/2-i)+fabs(101/2-j)<=101/2)
sum+=cnt;
}
}
printf("%d\n",sum);
return 0;
} 【答案】26020201
2. 【分析】DFS/全排列
根据题意,用0~7这8个数组成首位不为0的整数,可知这是一个对8个数的全排列。不过这里的全排列和之前的不太一样:首位不能为0,此外还需要使用一个数字num记录全排列的结果(num=a[0]*10^7+a[1]*10^6+...+a[6]*10^1+a[7]*10^0),以便后续进行素数判定。最后输出组成的素数个数。
法一:全排列
#include
#include
#include
using namespace std;
int a[9]={0,1,2,3,4,5,6,7};
int ans=0;
int is_prime(int n)
{
int i;
for(i=2;i<=sqrt(n);i++)
{
if(n%i==0)
return 0;
}
return 1;
}
int mypow(int a,int x)
{
int i;
int sum=1;
for(i=1;i<=x;i++)
sum*=a;
return sum;
}
int main()
{
int i;
int num;
do
{
num=0;
if(a[0]==0)
continue;
for(i=0;i<8;i++)
num+=(a[i]*mypow(10,7-i));
if(is_prime(num))
{
printf("%d\n",num);
ans++;
}
} while(next_permutation(a,a+8));
printf("ans = %d\n",ans);
return 0;
} 法二:DFS实现对8个数(0~7)的全排列
#include
#include
#include
int a[8],vis[8];
int ans=0;
int is_prime(int n)
{
int i;
for(i=2;i<=sqrt(n);i++)
{
if(n%i==0)
return 0;
}
return 1;
}
int mypow(int a,int x)
{
int i;
int mul=1;
for(i=1;i<=x;i++)
mul*=a;
return mul;
}
void dfs(int cur)
{
int i;
int num;
if(cur==8)
{
num=0;
for(i=0;i 法三:DFS,对上述算法的改进
添加一个数字的时候我们也可以通过 10*num+ i 完成把添加的数字放到数字末尾的操作 。对于第一位数字不能为 0 ,我们可以通过判定num 是否为 0 来判定第一位数字是否放 0;此外,使用"筛法"进行素数打表,在判定素数时直接查表即可。
#include
#include
#define MAX 77000000
int ans=0;
int vis[8],f[MAX];
void init()
{
int i,j;
memset(vis,0,sizeof(vis));
//筛法 素数打表(1-标记素数 0-标记非素数)
for(i=2;i 【答案】2668
3. 【分析】DFS
每一次搜索,找到两个相同的边界点,标记即可。检测边界点的方法也很简单,只需要一个点的四个方向中有一个点在地图外或者已经被标记,那么这个点就是边界点。
#include
#define MAX 25
int n; //地图大小
int map[MAX][MAX]; //连连看地图
int vis[MAX][MAX]; //地图各点的边界点标记(1-是边界点 0-不是边界点)
int maxscore; //最高得分
int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}}; //上下左右4个方向
//判断点(x,y)是否在地图内
int in(int x,int y)
{
return (x>=0 && x=0 && ymaxscore)
maxscore=cursc;
//找一对不同的边界点(i,j)与(k,l)
for(i=0;i 【答案】89
4. 【分析】数论
数论中的快速幂问题。求x^y mod p的值,结合给出的代码可确定以下思路:
将y转换为y/2的情况,直到y=0,即:当y为偶数时,x^y=((x^2)^(y/2)),当y为奇数时x^y=((x^2)^(y/2))*x,然后%p即可。
#include
int pw(int x, int y, int p) {
if (!y) {
return 1;
}
int res = pw(x*x%p,y/2,p);
if (y & 1) {
res = res * x % p;
}
return res;
}
int main() {
int x, y, p;
scanf("%d%d%d", &x, &y, &p);
printf("%d\n", pw(x, y, p));
return 0;
}
【参考答案】pw(x*x%p, y/2, p)
5. 【分析】数论
对于一个数的阶乘(分解成多个素数相乘),如果想末尾出现 0 的话,只有当 5 和 2 出现的时候,才会在末尾出现 0 。
因为 2 的个数一定比 5 多。所以我们就可以得出一个结论,一个数的阶乘,末尾 0 的个数就是看里面 5 的个数。
现在变成求 1 到 n 的因子有多少个 5。对于包含 1 个 5 的数字,就是 n/5,包含两个 5 的数字个数为 n / 25。。。通过 n = n / 5 的方式,每次剥掉一层 5。
#include
int main() {
int n, ans = 0;
scanf("%d", &n);
while (n) {
ans += n=n/5;
}
printf("%d\n", ans);
return 0;
}
【参考答案】n=n/5(+n赋值给ans 和 n除以5赋值给n同时进行)
6. 【分析】BFS+状态压缩
每个点状态用 d[x][y][state]表示,state表示每个宝藏是否获取的状态压缩。然后BFS即可。
#include
#include
#include
using namespace std;
char mat[11][11]={ //藏宝图
"0......9..",
"...X..0...",
".X..8..X..",
".7...X..6.",
".X..5.X...",
"..X....X..",
".....X..3.",
".X.X..1...",
".4....XX..",
"..X..X2...",
};
int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}}; //上下左右4个方向
struct node //定义藏宝图上的点
{
int x; //横坐标
int y; //纵坐标
int s; //状态
node(int xx,int yy,int ss):x(xx),y(yy),s(ss){}
};
int d[11][11][1<<10]; //点(x,y)的状态
//判断点(x,y)是否在地图内,且是否可走
int in(int x,int y)
{
return (x>=0 && x<10 && y>=0 && y<10 && mat[x][y]!='X');
}
void bfs()
{
int i;
int x,y,s; //当前点对应的状态
int tx,ty,ts; //当前点的邻接点(上/下/左/右)对应的状态
queue q;
memset(d,-1,sizeof(d));
q.push(node(0,0,0));
d[0][0][0]=0;
while(!q.empty())
{
x=q.front().x;
y=q.front().y;
s=q.front().s;
q.pop();
for(i=0;i<4;i++)
{
tx=x+dir[i][0];
ty=y+dir[i][1];
ts=s;
if(in(tx,ty))
{
if(mat[tx][ty]>='0' && mat[tx][ty]<='9')
ts=s|(1<<(mat[tx][ty]-'0'));
if(d[tx][ty][ts]==-1)
{
d[tx][ty][ts]=d[x][y][s]+1;
q.push(node(tx,ty,ts));
}
}
}
}
}
int main()
{
bfs();
cout< 【答案】48
7. 【分析】栈的巧妙应用(结合STL)
用栈来维护每次合并完的数,每入栈一个数以后栈顶和次栈顶比较,如果可以合并就合并为新的栈顶,并且再次与次栈顶比较直至无法合并(不排除当前栈顶元素可以与次栈顶甚至次栈顶后面的元素进行“合并”操作的可能),然后在合并过程中统计次数即可。
#include
#include
using namespace std;
int n,x;
int ans=0; //最大操作次数
stack st;
int main()
{
int i;
cin>>n;
for(i=0;i>x;
//将x与当前栈顶元素st.top()比较,若栈不空且st.top()比x大1,则合并一次(此时即当前栈顶元素出栈)
//然后x与次栈顶比较,以此类推,直到不满足栈不空且st.top()比x大1
while(!st.empty() && st.top()-x==1)
{
st.pop();
ans++;
}
//若栈不空且x比st.top()大1,则合并一次
//(此时即x"出栈",也就是忽略此x继续看下一个输入的x 但栈不发生任何变化)
if(!st.empty() && x-st.top()==1)
ans++;
//其他情况(x为第一个元素或不满足上述两种情况):将x入栈
else
st.push(x);
}
cout< 8. 【分析】
9. 【分析】一维几何问题+前缀和+GCD
考虑两对相邻点距离怎么由不同的通过加点变为全部相同,也就是对线段进行分割,分割成相同长度的若干段,这个长度最大也就是原来两条线段长度的最大公约数,我们先对点排好序然后做差,得到相邻点距离,因为最多允许有一段距离跟其它不同,可以枚举不同的是哪一段,对其它段求最大公约数。
因此,为了快速求出这个值,可以运用前缀和的思路,预处理出前缀 GCD 和后缀 GCD ,那么其它段的 GCD 就可以通过这两个 GCD 再求一遍 GCD 得到。得到分割后的距离后,每一段需要加的点就可以算了,但是如果每一次都去看每一段要加多少点还是太慢了,我们可以预处理得到最左点和最右点的距离,减去枚举中的那一段,再除以最大公约数得到一共会被分成多少小段,需要加的点数就是这个数字减去原来有多少段,也就是减去 n - 2。
10. 【分析】计数DP
可设dp[n][k]表示将正整数n分解为不多于k个正整数相加的形式的方案数。根据题意,应分以下4种情况讨论:
1°n=1 或 k=1:n=1时只有"1=1"这1种分解方案;k=1时只有"n=n"这1种分解方案,故方案数=1;
2°n 3°n>k:根据"是否将n恰好分解为k个正整数相加的形式"(上界),进行讨论: 1°°将n恰好分解为k个正整数相加的形式:此时分解出的每个正整数t都满足t>=1,故相当于将分解出的k个数"都减去1",即相当于dp[n-k][k],也就是将正整数n-k分解为不多于k个正整数相加的形式的方案数; 2°°将n分解为小于k个正整数相加的形式:此时即dp[n][k-1],也就是将正整数n分解为不多于k-1个正整数相加的形式的方案数; 故方案数=dp[n-k][k]+dp[n][k-1]; 4°n=k:总体与3°相同,但将n恰好分解为k个正整数相加的形式时,只有"n=n/k+n/k+...+n/k"这1种分解方案,故方案数=1+dp[n][k-1]。 综上,可得以下结论:![]()
#include