CNTK与深度强化学习笔记之一： 环境搭建和基本概念

如需转载，请指明出处。

---

前言

深度强化学习是人工智能当前的热点，CNTK也是微软力推的深度学习框架，2.x版本比之前有了长足的进步。目前国内将这两者融合起来的文章还不多。因此写作了这个学习笔记，希望能对大家有所帮助。

硬件，开发环境以及CNTK安装

CNTK可能是为数不多的在Windows平台同样支持CUDA和cuDNN加速的框架了。CNTK某些示例，虽然在CPU的环境下面也可以运行，但是速度实在是太慢了。因此推荐支持CUDA的Nvidia GPU，支持列表这里可以查到：CUDA GPUs。从列表中可以看到，如果想要买个游戏本做深度学习，GeForce GTX 1060是移动版本里面最便宜的支持CUDA的GPU。我正是使用了这个型号的游戏本。大概测试了一下CPU和GPU训练的性能差别，在用CNTK的ConvNet的示例训练MNIST时，使用GPU一个Epoch在2秒以内，使用“nvidia-smi -l 1”命令查看GPU的使用率，在95%以上。CPU（i7-7700HQ）需要大概50秒，使用率达到了100%。

开发环境需要在Ubuntu上面（推荐使用Ubuntu 14.04或者Ubuntu 16.04，本文使用的是Ubuntu 16.04），并且推荐使用Anaconda3的最新版本（本文使用的是Anaconda3-4.4.0，Python 3.6版本）。必须用Ubuntu的原因是，官方的DQN示例使用了gym。gym是由OpenAI开发的工具集，提供了强化学习中的环境（environment）接口，用来开发和对比强化学习算法。gym目前只支持Linux（只有有限的环境可以在Windows上面运行）。gym的安装配置官方文档也很清楚了：gym。

需要说明的是，Ubuntu 16.04默认的是开源版本的驱动，不支持GeForce GTX 1060，需要安装Nvidia的官方闭源驱动。我直接使用了Ubuntu的repo，命令"sudo apt-get install nvidia-375"就可以了。如果需要最新的驱动，也可以去Nvidia下载。用apt-get安装的另外一个好处是CUDA也会被一同安装。自己下载驱动的话需要安装CUDA。

CNTK官方文档给出了非常详细的安装过程，这里就不再重复。请参考CNTK的主页： CNTK。本文写作的时候，CNTK的版本是2.1（2017-07-31. CNTK 2.1）。

深度强化学习和DQN

目前我阅读到的，讲解深度强化学习最好的一篇文章来自Tambet Matiisen的DEMYSTIFYING DEEP REINFORCEMENT LEARNING。以下的内容基本上是对这篇文章的精简翻译（去掉少许内容并且加上我自己的理解）。

深度强化学习

2013年12月19日，DeepMind公司在Arxiv上发表了一篇论文：Playing Atari with Deep Reinforcement Learning。论文展示了他们如何使用强化学习，仅仅通过屏幕像素和分数作为奖赏，让电脑玩2600个雅达利的视频游戏。这个结果的意义在于，这些游戏和游戏要达到的目标都是不同的，并且是设计来挑战人类的。论文中提到的模型，不需要任何改变，就可以用来学习七个不同的游戏，并且在其中三个游戏中，模型的成绩比人类还好。这是迈向通用人工智能（强人工智能）的第一步：AI可以适应不同的环境，而不是限定于某个领域，例如玩象棋。发表了这个论文之后，DeepMind立刻就被Google收购了，并且一直引领了深度学习的研究。2015年2月，DeepMind又在自然杂志封面发表了论文Human-level control through deep reinforcement learning。在该论文中，DeepMind将同样的模型用到了49个游戏中，并且有半数取得了超人的成绩。

深度学习和强化学习的结合，无疑是近几年人工智能领域的热点。按照Yoshua Bengio的观点，目前的深度学习和所谓智能系统的表现，表明当前我们只做到了非常肤浅的部分，还远远没有触及智能的本源。我们必须去研究机器如何观察世界、理解世界，研究高层抽象，进行认知方面的探索。这个世界既包括真实世界，也可以是简单如视频游戏的虚拟环境。详见Andrew Ng对Bengio的访谈视频：Heroes of Deep Learning: Andrew Ng interviews Yoshua Bengio。后面我们也可以看到，用深度强化学习处理问题，更加的自然。

将深度学习和强化学习结合，有几个问题需要解决，后面的内容详细探讨这些问题：

1. 强化学习的主要挑战：功劳分配问题(credit assignment problem)，以及探索和开发困境（exploration-exploitation dilemma，也有翻译为探索和利用）。
2. 如何用数学形式表示深度学习问题：MDP（马尔科夫决策过程，Markov Decision Process）。
3. 如何形成长期策略：折扣的未来奖励（discounted future reward）。
4. 如何估计和逼近未来奖励：Q-learning算法。
5. 如何表示巨大的状态空间：深度神经网络。
6. 如何稳定学习：经历重放技术（experience replay technique）。

强化学习

考虑Breakout这个打砖块游戏。假定我们要教一个神经网络玩这个游戏。网络的输入应该是屏幕图像，输出应该是三个动作：左，右和发射球。如下图：

我们可能想到的是，这个问题可以作为一个分类问题，每个游戏屏幕对应一个动作。但是这样我们就需要大量的训练样本。当然我们可以找高手来玩并且录制游戏，但是这样不是人类真正如何学习的。我们不需要别人上百万次的告诉我们，哪个屏幕应该如何应对。我们只需要偶尔有点反馈说我们做对了，然后我们自己就可以搞明白怎么玩了。

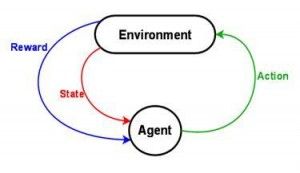
这就是强化学习要解决的问题。强化学习介于监督学习和非监督学习之间。监督学习需要每个训练数据都被标注，而非监督学习完全不需要标注。强化学习有稀疏的时延的标注，即奖励（Reward）。Agent从这些奖励中，学习如何与环境（Environment）互动。

这个概念是很直观的，但是在实践中有很多挑战。例如当我们击中了某个砖块并拿到了一个分数奖励，它通常跟刚刚拿到奖励之前的动作没有关系，所有需要的工作都已经完成了。这被称为功劳分配问题（credit assignment problem），例如，之前的哪些动作（actions）是获得奖励的原因，并且在多大程度上。

当使用某个策略得到了一些奖励，我们应该继续使用这个策略，还是应该尝试一些新的可能产生更好结果的策略？这被称为探索和开发困境（exploration-exploitation dilemma）：我们应该继续开发并且最大化已知策略，还是应该探索可能的更好策略。

###马尔科夫决策过程（MDP）

如何表示一个强化学习问题，使得我们可以推演它呢？最通用的方法是MDP。假定有一个Agent，被至于一个环境中（例如Breakout游戏）。环境被至于一个确定的状态（挡板的位置，球的位置和方向，存在的砖块等等）。Agent在Environment中可以执行一些Action（例如移动挡板到左边或者右边）。这些Action可能产生Reward（例如分数增加）。Action使得Environment发生State迁移，Agent可以执行另外一个Action，如此往复。选择这些Action的规则被成为策略。Environment通常是随机的，意味着下一个State可能是随机的（例如，当我们损失了一个球，发射一个新的球，它会飞向一个随机的方向）。

State和Action的合集，加上从一个State转换到另一个State，以得到Reward的策略，构成了MDP。一段这个过程（例如一局游戏）组成了有限的State，Action和Reward的序列。

\\(s_0, a_0, r_1, s_1, a_1, r_2, s_2, …, s_{n-1}, a_{n-1}, r_n, s_n\\)

这里\\(s_i\\)代表State，\\(a_i\\)是Action，\\(r_{i+1}\\)是执行Action之后的Reward。这段序列结束于最终状态\\(s_n\\)（例如游戏结束屏幕）。马尔科夫决策过程依赖于马尔科夫假设，即下一个State \\(s_{i+1}\\)只依赖于当前State \\(s_i\\)，与之前的State和Action无关。

折扣的未来奖励

为了能有好的长期结果，我们需要考虑的不仅仅是当前的Reward，并且还有将会得到的Reward。但是如何做到呢？

在一个马尔科夫过程中，我们可以很容易的计算一段序列的全部Reward：

\\(R=r_1+r_2+r_3+…+r_n\\)

同理，\\(t\\)之后所以的Reward，可以表示为：

\\(R_t=r_t+r_{t+1}+r_{t+2}+…+r_n\\)

但是因为环境是随机的，我们永远也没有办法保证，即使我们执行了相同的Action序列，我们还可以得到相同的Reward。序列进行的越远，分歧可能会越大。因此，通常都会使用折扣的未来奖励：

\\(R_t=r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}…+\gamma^{n-t} r_n\\)

这里\\(\gamma\\)是折扣系数，取值在0和1之间：越远的Reward，我们越少考虑。容易看出，\\(t\\)之后的折扣的未来奖励，可以用\\(t_{+1}\\)表示：

\\(R_t=r_t+\gamma (r_{t+1}+\gamma (r_{t+2}+…))=r_t+\gamma R_{t+1}\\)

如果设置\\(\gamma=0\\)，那么我们的策略是短视的，只依赖于当前的Reward。如果想平衡当前和将来Reward，一般设置\\(\gamma=0.9\\)。如果我们的环境是确定的，同样的Action序列总是得到相同的Reward，那么可以设置\\(\gamma=1\\)。

Agent的一个好的策略，是总去选择折扣的未来奖励最大的Action。

Q-learning算法

Q-learning算法中，定义了一个函数\\(Q(s,a)\\)，表示在状态\\(s\\)，采取动作\\(a\\)之后的折扣的未来奖励，然后在此基础上继续优化。

\\(Q(s_t,a_t)=max_{\pi} R_{t+1}\\)

对于\\(Q(s,a)\\)，应该这样理解：在状态\\(s\\)采取动作\\(a\\)之后，游戏结束时能拿到的最好分数。它被称为\\(Q\\)函数（Q-function），因为它表示了在某个State下面，某个Action的质量。这听起来有点令人费解。我们知道当前的State和Action，但是不知道下面的State和Action，如何才能估计游戏结束时候的分数？我们确实不能。但是理论上，我们可以假定有这样一个函数。

那么这个函数应该是什么样子呢？假定在状态\\(s\\)，要决定是采取动作\\(a\\)还是\\(b\\)，我们想选择一个动作，使得游戏结束时候的分数最高。当使用Q-function时，答案就很简单：取Q-value最大的动作：

\\(\pi(s) =argmax_a Q(s,a)\\)

这里\\(\pi(s) \\)代表策略，即我们在每个State，选择Action的规则。

但是我们如何得到Q-function？让我们先看一下一个状态转移的情况：\\(\\)，我们可以用下一个状态\\(s’\\)的Q-value，来表示状态\\(s\\)和动作\\(a\\)的Q-value：

\\(Q(s,a)=r + \gamma max_{a’}Q(s’,a’)\\)

这个方程被称为贝尔曼方程：当前State和Action的最大的未来奖励，等于现在的奖励加上下一个状态的最大未来奖励。

Q-learning主要的思想是，我们可以用贝尔曼方程，迭代逼近Q-function。最简单的实现是把Q-function函数实现为一个表格（Q-table），State是行，Action是列。那么Q-learning算法的伪代码如下：

initialize Q[numstates,numactions] arbitrarily
observe initial state s
repeat
	select and carry out an action a
	observe reward r and new state s'
    Q[s,a] = Q[s,a] + α(r + γmaxa' Q[s',a'] - Q[s,a])
    s = s'
until terminated

即从初始状态\\(s\\)开始，从Q-table中遍历所以的行动\\(a\\)，查看\\(a\\)对应的新状态\\(s’\\)，用新状态\\(s’\\)最大的奖励\\(r\\)，更新当前\\(Q[s,a]\\)。\\(α\\)是学习率。当学效率为1时，上面伪代码的等式，就完全和贝尔曼方程一样了。\\(maxa’ Q[s’,a’]\\)在初始阶段只是一个估计值，可能完全是错误的，但是随着迭代的进行，这个估计值会越来越精确。已经被证明，当迭代足够多次以后，\\(Q\\)函数会收敛，并且得到真实的值（Q-value）。

Deep Q Network(DQN)

上面的模型中，打砖块游戏的环境State，是由挡板的位置，球的位置和方向，还有每个砖块的位置定义的。但是这种直观的定义是游戏相关的（记得前面说过DeepMind只需要一个模型就可以玩49个游戏吗？）。那么我们能不能给出更加通用的，适合所有游戏的模型哪？一个明显的选择是用屏幕像素：隐含了所有的游戏状态，除了球的速度和方向，但是用两个连贯的屏幕就可以解决。

如果我们使用DeepMind论文中相同的预处理方法，截取四个最新的屏幕图像，将大小调整为84x84，并且转换成256级灰度，那么我们有\\(256^{84 \times 84 \times 4} \approx 10^{{67970}\\)个状态。相当于上面的Q-table有\\(10}{67970}\\)行。这个数目实在是太大了，并且某些状态可能永远也不能被访问到。因此这个方法不可行。

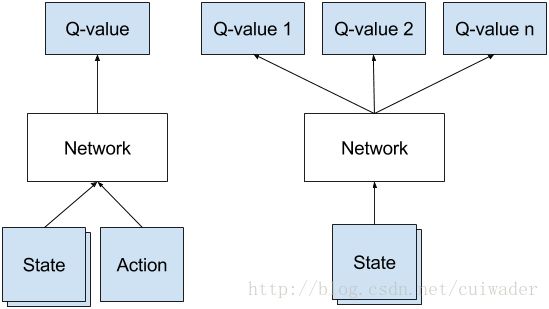
这里就需要用到深度学习了。神经网络（NN）特别适合结构化数据的特征提取
。我们可以用NN来表示Q-function，将state（四个游戏屏幕）和action作为输入，输出为相应的Q-value。我们也可以将一个游戏屏幕作为输入，输出为每个可能action的Q-value。后面这种方法更有优势，因为如果我们想更新Q-value，或者选择Q-value最大的action，我们只需要对网络前向传播一次，所有action的Q-value就都有了。下图是两种方法的区别：

DeepMind使用的网络结构如下：

这是一个包含了3个卷积层和两个连接层的CNN，不过没有池化层。这个也很好理解，因为池化层提供了平移不变性（translation invariance）：网络对对象在图像中的位置不敏感。但是对于游戏来说，小球的位置对于我们决定reward是至关重要的！我们不能丢弃这个信息！

网络的输入是84x84灰度的游戏屏幕，输出是每个可能状态的Q-value，可以是实数。这是一个回归任务，可以用简单的平方误差损失作优化。

经历重放

现在我们可以在每个状态下面，使用CNN，逼近Q-function，并用Q-learning估算每个state的未来reward。但是实际上，用非线性函数去逼近Q-value不是很稳定。使Q-value收敛，有很多技巧，并且还需要很长的时间（在一个GPU上面，可能需要一周）。

一个最重要的技巧是经历重放。在玩游戏的过程中，所有经历过的\\(\\)都被存储在重放内存中。当训练网络的时候，重放内存中会被随机采样，来替代最近的状态转换。这样就打破了其后训练样本的相关性，从而避免了网络进入一个局部最小值。并且经历重放使得训练变得和通常的监督学习类似，这样可以简化调试和测试。其实人类玩游戏也是这样的。

探索和开发困境

Q-learning解决了功劳分配问题：倒流时光反向传播reward，直到到达真正引起reward的决策点（通过折扣的未来奖励）。现在来看看怎么解决探索和开发困境。

首先，Q-table或者Q-network是随机初始化的，随后初始的预测也是随机的。如果我们选择了最高的Q-value，那么这个选择也是随机的，相当于Agent在进行探索。当Q-function收敛的时候，它会返回稳定的Q-value，探索随之减少。所以我们可以认为，探索是Q-learning算法的一部分。但是这个探索是贪婪的：探索停止于找到的第一个可用策略。

ε-greedy exploration可以简单有效的修正这个问题。ε是随机选择一个Action的概率，否则用贪婪的办法选择Q-value最高的Action。即按照一定概率，选择随机的Action。

深度Q-learning算法

前面给出了基于Q-table的Q-learning算法的伪代码，现在看看带经历重放的深度Q-learning的算法：

initialize replay memory D
initialize action-value function Q with random weights
observe initial state s
repeat
    select an action a
        with probability ε select a random action
        otherwise select a = argmaxa’Q(s,a’)
    carry out action a
    observe reward r and new state s’
    store experience  in replay memory D

    sample random transitions  from replay memory D
    calculate target for each minibatch transition
        if ss’ is terminal state then tt = rr
        otherwise tt = rr + γmaxa’Q(ss’, aa’)
    train the Q network using (tt - Q(ss, aa))^2 as loss

    s = s'
until terminated

从伪代码可以看到，经历重放就是从重放内存中，随机采样，用采样的State的Q-value去训练网络。

除了这个算法，DeepMind还使用了很多其它的技巧，超出了本文的介绍范围。这个算法最神奇之处在于，它确实学习了。想想看，Q-function是随机初始化的。它一开始的输出都是垃圾，没有任何意义。我们把这个垃圾（下一个State的最大Q-value）作为网络的目标，偶尔加入一点Reward。听起来很愚蠢，它怎么能学到点有意义的东西呢？实际上，它学到了。

和最早的版本相比，Q-learning已经有了很大的发展，包括 Double Q-learning, Prioritized Experience Replay, Dueling Network Architecture和 extension to continuous action space等。不过请注意，深度Q-learning已经被Google申请了专利。

公式看的头晕，还是看看代码吧：CNTK与深度强化学习笔记之二： Cart Pole游戏示例