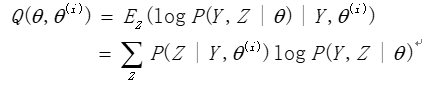EM算法详解
极大似然估计
极大似然的本质是找出与样本分布最接近的概率分布模型,它是一种用样本来估计概率模型参数的方法。下面以二项分布和高斯分布为例。
1.二项分布
例如,进行抛硬币实验,十次抛硬币的结果是: 正 正 反 正 正 正 反 反 正 正 正正反正正正反反正正 正正反正正正反反正正假设p是每次抛硬币结果为正的概率,则,得到实验结果的概率是,
P = p p ( 1 − p ) p p p ( 1 − p ) ( 1 − p ) p p = p 7 ( 1 − p ) 3 \begin{array}{l} P = pp(1 - p)ppp(1 - p)(1 - p)pp\\\\ \;\;\;\; = {p^7}{(1 - p)^3} \end{array} P=pp(1−p)ppp(1−p)(1−p)pp=p7(1−p)3
而极大似然估计的原理就是让得到实验结果的概率最大,即求得一个参数p使得整个式子最大。
那么对上式求导,得, P ′ = 7 − 10 p = 0 {P^{'}} = 7 - 10p = 0 P′=7−10p=0,所以求得的p=0.7,即在极大似然估计下求得的正面朝上的概率是0.7。这是一个符合样本分布的结果,因为在10次实验中,有7次是朝上的。
有人说这可能与平常我们认为的不同,对于抛硬币正反的概率不应该是0.5吗?即,每次出现正反的概率都一样才对。那么,这里算出的正面朝上的概率为0.7其实是在极大似然估计下的参数,这完全是基于样本获得的,样本有7次朝上,总共做了10次实验,那么显然,通过样本计算出的正面朝上的概率就是0.7,这就体现了极大似然估计以样本来算参数的原理。
对上述问题进行抽象。在抛硬币的实验中,进行N次独立的实验,n次朝上,N-n次朝下,假设朝上的概率为p,则其似然函数为,
f = p n ( 1 − p ) N − n f = {p^n}{(1 - p)^{N - n}} f=pn(1−p)N−n
一般,似然函数为连乘的形式,不好求导,所以,一般对似然函数取对数,即对数似然函数,
log ( f ) = log ( p n ( 1 − p ) N − n ) = n log ( p ) + ( N − n ) log ( 1 − p ) \log (f) = \log ({p^n}{(1 - p)^{N - n}}) = n\log (p) + (N - n)\log (1 - p) log(f)=log(pn(1−p)N−n)=nlog(p)+(N−n)log(1−p)
对上式求导,即, ∂ ( log f ) ∂ p = n p − N − n 1 − p = 0 \frac{{\partial (\log f)}}{{\partial p}} = \frac{n}{p} - \frac{{N - n}}{{1 - p}} = 0 ∂p∂(logf)=pn−1−pN−n=0,求得, p = n N p = \frac{n}{N} p=Nn。这个结果很显然是符合实验结果分布的。
2.高斯分布
给定一组样本 x 1 , x 2 , ⋯ , x n {x_1},{x_2}, \cdots ,{x_n} x1,x2,⋯,xn,已知它们服从高斯分布 N ( u , σ ) N(u,\sigma ) N(u,σ),试用极大似然估计估计它们的参数 u , σ u,\sigma u,σ。
已知高斯分布的概率密度函数为,
f ( x ) = 1 2 π σ e − ( x − u ) 2 2 σ 2 f(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(x - u)}^2}}}{{2{\sigma ^2}}}}} f(x)=2πσ1e−2σ2(x−u)2
将样本带入,建立极大似然函数,
L ( x ) = ∏ i = 1 n 1 2 π σ e − ( x i − u ) 2 2 σ 2 L(x) = \prod\limits_{i = 1}^n {\frac{1}{{\sqrt {2\pi } \sigma }}} {e^{ - \frac{{{{({x_i} - u)}^2}}}{{2{\sigma ^2}}}}} L(x)=i=1∏n2πσ1e−2σ2(xi−u)2
取对数似然函数,
l ( x ) = log ( L ( x ) ) = log ( ∏ i = 1 n 1 2 π σ e − ( x − u ) 2 2 σ 2 ) = ∑ i = 1 n log ( 1 2 π σ e − ( x − u ) 2 2 σ 2 ) = ∑ i = 1 n log ( 2 π σ 2 ) − 1 2 + ∑ i = 1 n − ( x − u ) 2 2 σ 2 = − n 2 log ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x − u ) 2 \begin{array}{l} l(x) = \log (L(x)) = \log (\prod\limits_{i = 1}^n {\frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(x - u)}^2}}}{{2{\sigma ^2}}}}}} )\\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \; = \sum\limits_{i = 1}^n {\log (\frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(x - u)}^2}}}{{2{\sigma ^2}}}}})} \\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \; = {\sum\limits_{i = 1}^n {\log (2\pi {\sigma ^2})} ^{ - \frac{1}{2}}} + \sum\limits_{i = 1}^n { - \frac{{{{(x - u)}^2}}}{{2{\sigma ^2}}}} \\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \; = - \frac{n}{2}\log (2\pi {\sigma ^2}) - \frac{1}{{2{\sigma ^2}}}\sum\limits_{i = 1}^n {{{(x - u)}^2}} \\ \end{array} l(x)=log(L(x))=log(i=1∏n2πσ1e−2σ2(x−u)2)=i=1∑nlog(2πσ1e−2σ2(x−u)2)=i=1∑nlog(2πσ2)−21+i=1∑n−2σ2(x−u)2=−2nlog(2πσ2)−2σ21i=1∑n(x−u)2
对 u , σ u,\sigma u,σ求偏导,
∂ l ( x ) ∂ u = 1 σ 2 ∑ i = 1 n ( x i − u ) = 1 σ 2 ( ∑ i = 1 n x i − n u ) = 0 \frac{{\partial l(x)}}{{\partial u}} = \frac{1}{{{\sigma ^2}}}\sum\limits_{i = 1}^n {({x^i} - u)} = \frac{1}{{{\sigma ^2}}}(\sum\limits_{i = 1}^n {{x^i} - } nu) = 0 ∂u∂l(x)=σ21i=1∑n(xi−u)=σ21(i=1∑nxi−nu)=0 ∂ l ( x ) ∂ σ = − n σ + 1 σ 3 ∑ i = 1 n ( x i − u ) 2 = 0 \frac{{\partial l(x)}}{{\partial \sigma }} = - \frac{n}{\sigma } + \frac{1}{{{\sigma ^3}}}\sum\limits_{i = 1}^n {{{({x_i} - u)}^2}} = 0 ∂σ∂l(x)=−σn+σ31i=1∑n(xi−u)2=0
求得的结果如下,
u = 1 n ∑ i = 1 n x i σ 2 = 1 n ∑ i = 1 n ( x i − u ) 2 \begin{array}{l} u = \frac{1}{n}\sum\limits_{i = 1}^n {{x^i}} \\\\ {\sigma ^2} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - u)}^2}} \end{array} u=n1i=1∑nxiσ2=n1i=1∑n(xi−u)2
上述结论与矩估计是一致的,并且意义很直观:样本的均值即高斯分布的均值,样本的伪方差(不说方差,是因为无偏估计的方差是除以n-1的,而不是这里的n)为高斯分布的方差。
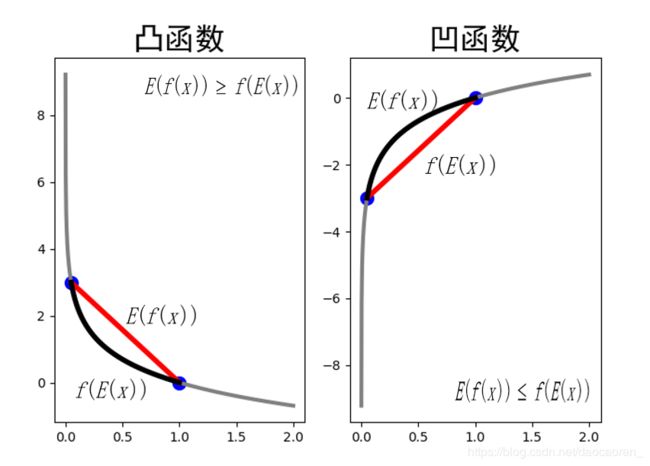
Jensen不等式
- 若f函数为凸函数:
- 基本的Jensen不等式 :
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x + (1 - \theta )y) \le \theta f(x) + (1 - \theta )f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) - k维的Jensen不等式 :
若 θ 1 , ⋯ , θ k ≥ 0 , θ 1 + ⋯ + θ k = 1 {\theta _1}, \cdots ,{\theta _k} \ge 0,{\theta _1} + \cdots + {\theta _k} = 1 θ1,⋯,θk≥0,θ1+⋯+θk=1,则,
f ( θ 1 x 1 + ⋯ + θ k x k ) ≤ θ 1 f ( x 1 ) + ⋯ + θ k f ( x k ) f({\theta _1}{x_1} + \cdots + {\theta _k}{x_k}) \le {\theta _1}f({x_1}) + \cdots + {\theta _k}f({x_k}) f(θ1x1+⋯+θkxk)≤θ1f(x1)+⋯+θkf(xk)
换一个看待的方式,把 θ \theta θ看作随机变量,则上式的含义就是对于凸函数而言,期望的函数小于等于函数值得期望,即,
f ( E ( x ) ) ≤ E ( f ( x ) ) f(E(x)) \le E(f(x)) f(E(x))≤E(f(x))
- 基本的Jensen不等式 :
- 若f函数为凹函数: 结论恰好相反,即,
f ( θ 1 x 1 + ⋯ + θ k x k ) ≥ θ 1 f ( x 1 ) + ⋯ + θ k f ( x k ) f({\theta _1}{x_1} + \cdots + {\theta _k}{x_k}) \ge {\theta _1}f({x_1}) + \cdots + {\theta _k}f({x_k}) f(θ1x1+⋯+θkxk)≥θ1f(x1)+⋯+θkf(xk)
三硬币例子——隐变量
先看一个抛三硬币例子,假设有A,B,C这3枚硬币,它们正面向上的概率分别是 π , p 和 q \pi ,p和q π,p和q。进行如下的抛硬币实验:先抛硬币A,根据其结果选出硬币B和硬币C,正面选择硬币A,反面选C;然后抛选出的硬币,出现正面记作1,出现反面记作0;独立重复n次实验,假设n=10,观测结果如下:1,1,0,1,0,0,1,0,1,1。若只知道观测到的硬币结果,而不知道抛硬币的过程,那么,如何来估计这三枚硬币正面朝上的概率。
上例中,一次实验结果是能直接观测到的(即B或C的结果),这就是观测变量(observable variable),这里记作随机变量y;而上例中硬币A的结果是观测不到的,这就是隐变量(latent variable),用随机变量z表示; θ = ( π , p , q ) \theta = (\pi ,p,q) θ=(π,p,q)是模型参数,即A,B,C这三枚硬币正面朝上的概率。
对上例进行建模,则模型可以写作,
P ( y ∣ θ ) = ∑ z P ( y , z ∣ θ ) = ∑ z P ( z ∣ θ ) P ( y ∣ z , θ ) = π p y ( 1 − p ) 1 − y + ( 1 − π ) q y ( 1 − q ) y \begin{array}{l} P(y|\theta ) = \sum\limits_z {P(y,z|\theta )} = \sum\limits_z {P(z|\theta )P(y|z,\theta )} \\ \;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \pi {p^y}{(1 - p)^{1 - y}} + (1 - \pi ){q^y}{(1 - q)^y} \end{array} P(y∣θ)=z∑P(y,z∣θ)=z∑P(z∣θ)P(y∣z,θ)=πpy(1−p)1−y+(1−π)qy(1−q)y
若将观测数据用 Y = { Y 1 , Y 2 , ⋯ , Y n } Y = \{ {Y_1},{Y_2}, \cdots ,{Y_n}\} Y={Y1,Y2,⋯,Yn}表示,未观测数据用 Z = { Z 1 , Z 2 , ⋯ , Z n } Z = \{ {Z_1},{Z_2}, \cdots ,{Z_n}\} Z={Z1,Z2,⋯,Zn}表示,则观测数据的似然函数为,
P ( Y ∣ θ ) = ∑ z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) P(Y|\theta ) = \sum\limits_z {P(Z|\theta )} P(Y|Z,\theta ) P(Y∣θ)=z∑P(Z∣θ)P(Y∣Z,θ)
对数似然函数为,
l ( y ) = log ( P ( Y ∣ θ ) ) = log ( ∑ z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) ) l(y) = \log (P(Y|\theta )) = \log (\sum\limits_z {P(Z|\theta )P(Y|Z,\theta )} ) l(y)=log(P(Y∣θ))=log(z∑P(Z∣θ)P(Y∣Z,θ))
因为log函数里有求和,又含有隐变量,所以不好求解导数,对于上述含有隐变量的极大似然估计,可以用EM算法求解。
EM算法推导
那么,EM算法其实就是对于上述含有隐变量的概率模型极大似然估计。
当面对一个含有隐变量的概率模型时,当然,目标还是极大化观测数据Y关于 θ \theta θ的似然函数,即,
l ( θ ) = log P ( Y ∣ θ ) = log ∑ z ( Y , Z ∣ θ ) = log ( ∑ z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) \begin{array}{l} l(\theta ) = \log P(Y|\theta ) = \log \sum\limits_z {(Y,Z|\theta )} \\ \;\;\;\;\;\;\ = \log (\sum\limits_z {P(Y|Z,\theta )P(Z|\theta )} ) \end{array} l(θ)=logP(Y∣θ)=logz∑(Y,Z∣θ) =log(z∑P(Y∣Z,θ)P(Z∣θ))
既然上式不好直接求解,那么就考虑迭代法求解。假设在第i次迭代后 θ \theta θ的估计值为 θ ( i ) {\theta ^{(i)}} θ(i)。那么,下次就希望新估计的 θ \theta θ值,可以使 l ( θ ) l(\theta ) l(θ)增加,即 l ( θ ( i + 1 ) ) > l ( θ ( i ) ) l({\theta ^{(i + 1)}}) > l({\theta ^{(i)}}) l(θ(i+1))>l(θ(i))。这样一步步迭代下去,就能达到极大值,为此,可以考虑两者之差,
l ( θ ) − l ( θ ( i ) ) = log ( ∑ z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) − log P ( Y ∣ θ ( i ) ) = log ( ∑ z P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) ≥ ( 凹 函 数 的 J e n s e n 不 等 式 ) ∑ Z P ( Z ∣ Y , θ ( i ) ) log ( P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) \begin{array}{l} l(\theta ) - l({\theta ^{(i)}}) = \log (\sum\limits_z {P(Y|Z,\theta )} P(Z{\rm{|}}\theta )){\rm{ - }}\log P(Y|{\theta ^{(i)}})\\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ = \log (\sum\limits_z {P(Z|Y,{\theta ^{(i)}})\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}}} ){\rm{ - }}\log P(Y|{\theta ^{(i)}})\\\\ \;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} \mathop \ge \limits^{(凹函数的Jensen不等式)} \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log (\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}})} {\rm{ - }}\log P(Y|{\theta ^{(i)}})\\ \;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array} l(θ)−l(θ(i))=log(z∑P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i)) =log(z∑P(Z∣Y,θ(i))P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))≥(凹函数的Jensen不等式)Z∑P(Z∣Y,θ(i))log(P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))
令,
B ( θ , θ ( i ) ) = l ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log ( P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) B(\theta ,{\theta ^{(i)}}) = l({\theta ^{(i)}}) + \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log (\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}})} {\rm{ - }}\log P(Y|{\theta ^{(i)}}) B(θ,θ(i))=l(θ(i))+Z∑P(Z∣Y,θ(i))log(P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))
则,
l ( θ ) ≥ B ( θ , θ ( i ) ) l(\theta ) \ge B(\theta ,{\theta ^{(i)}}) l(θ)≥B(θ,θ(i))
此时,函数 B ( θ , θ ( i ) ) B(\theta ,{\theta ^{(i)}}) B(θ,θ(i))是 l ( θ ) l(\theta ) l(θ)的一个下界函数。
则,任何可以使 B ( θ , θ ( i ) ) B(\theta ,{\theta ^{(i)}}) B(θ,θ(i))增大的 θ \theta θ,也可以使 l ( θ ) l(\theta ) l(θ)增大,为了使 l ( θ ) l(\theta ) l(θ)有尽可能大的增长,那么在第i+1次迭代中,应选择 θ ( i + 1 ) {\theta ^{(i + 1)}} θ(i+1)使得 B ( θ , θ ( i ) ) B(\theta ,{\theta ^{(i)}}) B(θ,θ(i))达到极大,即,
θ ( i + 1 ) = arg max θ B ( θ , θ ( i ) ) {\theta ^{(i + 1)}} = \arg \mathop {\max }\limits_\theta B(\theta ,{\theta ^{(i)}}) θ(i+1)=argθmaxB(θ,θ(i))
省去对 θ \theta θ的极大化而言是常数的项,有,
θ ( i + 1 ) = arg max θ l ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log ( P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) = arg max θ ∑ Z P ( Z ∣ Y , θ ( i ) ) log ( P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) = arg max θ ∑ Z P ( Z ∣ Y , θ ( i ) ) log ( P ( Y , Z ∣ θ ) ) = arg max θ Q ( θ , θ ( i ) ) \begin{array}{l} {\theta ^{(i + 1)}} = \arg \mathop {\max }\limits_\theta l({\theta ^{(i)}}) + \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log (\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}})} {\rm{ - }}\log P(Y|{\theta ^{(i)}})\\\\ \;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \arg \mathop {\max }\limits_\theta \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log } (P(Y|Z,\theta )P(Z{\rm{|}}\theta ))\\\\ \;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \arg \mathop {\max }\limits_\theta \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log } (P(Y,Z|\theta ))\\\\ \;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \arg \mathop {\max }\limits_\theta Q(\theta ,{\theta ^{(i)}}) \end{array} θ(i+1)=argθmaxl(θ(i))+Z∑P(Z∣Y,θ(i))log(P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))=argθmaxZ∑P(Z∣Y,θ(i))log(P(Y∣Z,θ)P(Z∣θ))=argθmaxZ∑P(Z∣Y,θ(i))log(P(Y,Z∣θ))=argθmaxQ(θ,θ(i))
算法描述如下,
EM算法的另一种推导
基于上述的分析过程,建立对数似然函数如下,
l ( θ ) = ∑ i = 1 N log P ( x ∣ θ ) = ∑ i = 1 N log ∑ z P ( x , z ∣ θ ) l(\theta ) = \sum\limits_{i = 1}^N {\log P(x|\theta )} = \sum\limits_{i = 1}^N {\log \sum\limits_z {P(x,z|\theta )} } l(θ)=i=1∑NlogP(x∣θ)=i=1∑Nlogz∑P(x,z∣θ)
若 Q i {Q_i} Qi是z的某一个分布,则有,
l ( θ ) = ∑ i = 1 N log ∑ z P ( x , z ∣ θ ) = ∑ i = 1 N log ∑ z i P ( x i , z i ∣ θ ) = ∑ i = 1 N log ∑ z i Q i ( z i ) P ( x i , z i ∣ θ ) Q i ( z i ) ≥ ∑ i = 1 N ∑ z i Q i ( z i ) log P ( x i , z i ∣ θ ) Q i ( z i ) \begin{array}{l} l(\theta ) = \sum\limits_{i = 1}^N {\log \sum\limits_z {P(x,z|\theta )} } \\\\ \;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{i = 1}^N {\log \sum\limits_{{z_i}} {P({x_i},{z_i}|\theta )} } \\\\ \;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{i = 1}^N {\log \sum\limits_{{z_i}} {{Q_i}({z_i})\frac{{P({x_i},{z_i}|\theta )}}{{{Q_i}({z_i})}}} } \\\\ \;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ge \sum\limits_{i = 1}^N {\sum\limits_{{z_i}} {{Q_i}({z_i})\log \frac{{P({x_i},{z_i}|\theta )}}{{{Q_i}({z_i})}}} } \end{array} l(θ)=i=1∑Nlogz∑P(x,z∣θ)=i=1∑Nlogzi∑P(xi,zi∣θ)=i=1∑Nlogzi∑Qi(zi)Qi(zi)P(xi,zi∣θ)≥i=1∑Nzi∑Qi(zi)logQi(zi)P(xi,zi∣θ)

因为要找到尽量靠近的下界(图像性质可知),所以就要使Jensen不等式的等号成立,则,
P ( x i , z i ∣ θ ) Q i ( z i ) = c ( c 是 常 数 ) \frac{{P({x_i},{z_i}|\theta )}}{{{Q_i}({z_i})}} = c(c是常数) Qi(zi)P(xi,zi∣θ)=c(c是常数)
进一步分析,
Q i ( z i ) ∝ P ( x i , z i ∣ θ ) ∑ z Q i ( z i ) = 1 } ⇒ Q i ( z i ) = P ( x i , z i ∣ θ ) ∑ z P ( x i , z i ∣ θ ) = P ( x i , z i ∣ θ ) P ( x i ∣ θ ) = P ( z i ∣ x i , θ ) \begin{array}{l} \left. {\begin{array}{l} {{Q_i}({z_i}) \propto P({x_i},{z_i}|\theta )}\\\\ {\sum\limits_z {{Q_i}({z_i}) = 1} } \end{array}} \right\}\\\\ \Rightarrow {Q_i}({z_i}) = \frac{{P({x_i},{z_i}|\theta )}}{{\sum\limits_z {P({x_i},{z_i}|\theta )} }}\\\\ \;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({x_i},{z_i}|\theta )}}{{P({x_i}|\theta )}}\\\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} = P({z_i}|{x_i},\theta ) \end{array} Qi(zi)∝P(xi,zi∣θ)z∑Qi(zi)=1⎭⎪⎬⎪⎫⇒Qi(zi)=z∑P(xi,zi∣θ)P(xi,zi∣θ)=P(xi∣θ)P(xi,zi∣θ)=P(zi∣xi,θ)
所以,当且仅当 Q i {Q_i} Qi取上式的条件概率时,推导过程中的Jensen不等式才能取等号。
此时,EM算法描述为,
| EM算法 |
|---|
| E步:对于每一个i,求, M步:更新 θ \theta θ 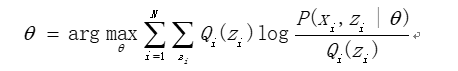 |
高斯混合模型(Gaussian Mixture Model,GMM)下的EM算法
首先,高斯混合分布如下,
p ( x ) = ∑ i = 1 K π i p ( x ∣ u i , Σ i ) p(x) = \sum\limits_{i = 1}^K {{\pi _i}p(x|{u_i},{\Sigma _i})} p(x)=i=1∑Kπip(x∣ui,Σi)
该分布总共由K个高斯分布组成,这里的 p ( x ∣ u i , Σ i ) p(x|{u_i},{\Sigma _i}) p(x∣ui,Σi)是多元高斯分布,
p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e − 1 2 ( x − u ) T Σ − 1 ( x − u ) p(x) = \frac{1}{{{{(2\pi )}^{\frac{n}{2}}}{{\left| \Sigma \right|}^{\frac{1}{2}}}}}{e^{ - \frac{1}{2}{{(x - u)}^T}{\Sigma ^{ - 1}}(x - u)}} p(x)=(2π)2n∣Σ∣211e−21(x−u)TΣ−1(x−u)
而高斯混合分布中的 π i {\pi _i} πi为第i个混合成分的“混合系数”,且 ∑ i = 1 K π i = 1 \sum\limits_{i = 1}^K {{\pi _i} = 1} i=1∑Kπi=1。
那么估计GMM的问题如下:已知随机变量X是由K个高斯分布混合而成,取各个高斯分布的概率为 π 1 , π 2 , ⋯ , π K {\pi _1},{\pi _2}, \cdots ,{\pi _K} π1,π2,⋯,πK,第i个高斯分布的均值为 u i {u_i} ui,方差为 Σ i {\Sigma _i} Σi。若观测到随机变量的一系列样本为 x 1 , x 2 , ⋯ , x N {x_1},{x_2}, \cdots ,{x_N} x1,x2,⋯,xN,试估计参数 θ = ( π , u , Σ ) \theta = (\pi ,u,\Sigma ) θ=(π,u,Σ)。
应用EM算法来估计GMM的参数。
1.E步:
Q i ( z i ) = P ( z i ∣ x i , θ ) = P ( z i , x i , θ ) P ( x i , θ ) = P ( x i ∣ z i , θ ) P ( z i , θ ) P ( x i , θ ) = P ( x i ∣ z i , θ ) P ( z i ) P ( x i ) = π k N ( x i ∣ u k , Σ k ) ∑ j = 1 K π j N ( x i ∣ u j , Σ j ) \begin{array}{l} {Q_i}({z^i}) = P({z_i}|{x_i},\theta )\\\\ \;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({z_i},{x_i},\theta )}}{{P({x_i},\theta )}}\\\\ \;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({x_i}|{z_i},\theta )P({z_i},\theta )}}{{P({x_i},\theta )}}\\\\ \;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({x_i}|{z_i},\theta )P({z_i})}}{{P({x_i})}}\\\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{\pi _k}N({x_i}|{u_k},{\Sigma _k})}}{{\sum\limits_{j = 1}^K {{\pi _j}N({x_i}|{u_j},{\Sigma _j})} }} \end{array} Qi(zi)=P(zi∣xi,θ)=P(xi,θ)P(zi,xi,θ)=P(xi,θ)P(xi∣zi,θ)P(zi,θ)=P(xi)P(xi∣zi,θ)P(zi)=j=1∑KπjN(xi∣uj,Σj)πkN(xi∣uk,Σk)
上式的含义为,样本 x i {x_i} xi由第k个高斯分布生成的概率,记作 γ i k {\gamma _{ik}} γik,则,
γ i k = π k N ( x i ∣ u k , Σ k ) ∑ j = 1 K π j N ( x i ∣ u j , Σ j ) {\gamma _{ik}} = \frac{{{\pi _k}N({x_i}|{u_k},{\Sigma _k})}}{{\sum\limits_{j = 1}^K {{\pi _j}N({x_i}|{u_j},{\Sigma _j})} }} γik=j=1∑KπjN(xi∣uj,Σj)πkN(xi∣uk,Σk)
2.M步:将高斯分布带入计算,
∑ i = 1 N ∑ z i Q i ( z i ) log P ( x i , z i ∣ π , u , Σ ) Q i ( z i ) = ∑ i = 1 N ∑ j = 1 K Q i ( z i = j ) log P ( x i ∣ z i = j , θ ) P ( z i = j ∣ θ ) Q i ( z i = j ) = ∑ i = 1 N ∑ j = 1 K γ i j log 1 ( 2 π ) n 2 ∣ Σ j ∣ 1 2 exp ( − 1 2 ( x i − u j ) T Σ j − 1 ( x i − u j ) ) ⋅ π j γ i j \begin{array}{l} \sum\limits_{i = 1}^N {\sum\limits_{{z_i}} {{Q_i}({z_i})\log \frac{{P({x_i},{z_i}|\pi ,u,\Sigma )}}{{{Q_i}({z_i})}}} } \\\\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{Q_i}({z_i} = j)} } \log \frac{{P({x_i}|{z_i} = j,\theta )P({z_i} = j|\theta )}}{{{Q_i}({z_i} = j)}}\\\\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\gamma _{ij}}\log \frac{{\frac{1}{{{{(2\pi )}^{\frac{n}{2}}}{{\left| {{\Sigma _j}} \right|}^{\frac{1}{2}}}}}\exp ( - \frac{1}{2}{{({x_i} - {u_j})}^T}\Sigma _j^{ - 1}({x_i} - {u_j})) \cdot {\pi _j}}}{{{\gamma _{ij}}}}} } \end{array} i=1∑Nzi∑Qi(zi)logQi(zi)P(xi,zi∣π,u,Σ)=i=1∑Nj=1∑KQi(zi=j)logQi(zi=j)P(xi∣zi=j,θ)P(zi=j∣θ)=i=1∑Nj=1∑Kγijlogγij(2π)2n∣Σj∣211exp(−21(xi−uj)TΣj−1(xi−uj))⋅πj
对均值求偏导,
∇ u l = ∑ i = 1 N γ i l Σ l − 1 ( x i − u l ) = 0 {\nabla _{{u_l}}} = \sum\limits_{i = 1}^N {{\gamma _{il}}\Sigma _l^{ - 1}({x_i} - {u_l})} = 0 ∇ul=i=1∑NγilΣl−1(xi−ul)=0则其均值为,
u l = ∑ i = 1 N γ i l x i ∑ i = 1 N γ i l {u_l} = \frac{{\sum\limits_{i = 1}^N {{\gamma _{il}}{x_i}} }}{{\sum\limits_{i = 1}^N {{\gamma _{il}}} }} ul=i=1∑Nγili=1∑Nγilxi
对方差求偏导
∇ Σ l = − 1 2 ∑ i = 1 N γ i l ( 1 Σ l − ( x i − u l ) ( x i − u l ) T Σ l 2 ) = 0 {\nabla _{{\Sigma _l}}} = - \frac{1}{2}\sum\limits_{i = 1}^N {{\gamma _{il}}(\frac{1}{{{\Sigma _l}}} - \frac{{({x_i} - {u_l}){{({x_i} - {u_l})}^T}}}{{\Sigma _l^2}})} = 0 ∇Σl=−21i=1∑Nγil(Σl1−Σl2(xi−ul)(xi−ul)T)=0则其方差为,
Σ l = ∑ i = 1 N γ i l ( x i − u l ) ( x i − u l ) T ∑ i = 1 N γ i l {\Sigma _l} = \frac{{\sum\limits_{i = 1}^N {{\gamma _{il}}({x_i} - {u_l}){{({x_i} - {u_l})}^T}} }}{{\sum\limits_{i = 1}^N {{\gamma _{il}}} }} Σl=i=1∑Nγili=1∑Nγil(xi−ul)(xi−ul)T
对 π \pi π的求解,使用拉格朗日乘子法,考虑 ∑ j = 1 K π j = 1 \sum\limits_{j = 1}^K {{\pi _j} = 1} j=1∑Kπj=1, L ( π ) = ∑ i = 1 N ∑ j = 1 K γ i k log π j + β ( ∑ j = 1 K π j − 1 ) L(\pi ) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\gamma _{ik}}\log {\pi _j} + \beta (\sum\limits_{j = 1}^K {{\pi _j} - 1} )} } L(π)=i=1∑Nj=1∑Kγiklogπj+β(j=1∑Kπj−1)
对 π j {\pi _j} πj求导,
∂ L ∂ π j = ∑ i = 1 N γ i j π j + β = 0 π j = ∑ i = 1 N γ i j − β ∑ j = 1 K π j = ∑ j = 1 K ∑ i = 1 N γ i j − β = 1 − β ∑ i = 1 N ∑ j = 1 K γ i j = 1 − β ∑ i = 1 N 1 = 1 − β N = 1 − β = N π j = ∑ i = 1 N γ i j − β = ∑ i = 1 N γ i j N \begin{array}{l} \frac{{\partial L}}{{\partial {\pi _j}}} = \sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{{\pi _j}}} + \beta = 0} \\\\ {\pi _j} = \sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{ - \beta }}} \\\\ \sum\limits_{j = 1}^K {{\pi _j} = \sum\limits_{j = 1}^K {\sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{ - \beta }}} } } \\\\ \;\;\;\;\;\;\;\;\;\; = \frac{1}{{ - \beta }}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\gamma _{ij}}} } \\\\ \;\;\;\;\;\;\;\;\;\; = \frac{1}{{ - \beta }}\sum\limits_{i = 1}^N 1 \\\\ \;\;\;\;\;\;\;\;\;\; = \frac{1}{{ - \beta }}N = 1\\\\- \beta = N\\\\{\pi _j} = \sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{ - \beta }}} = \frac{{\sum\limits_{i = 1}^N {{\gamma _{ij}}} }}{N} \end{array} ∂πj∂L=i=1∑Nπjγij+β=0πj=i=1∑N−βγijj=1∑Kπj=j=1∑Ki=1∑N−βγij=−β1i=1∑Nj=1∑Kγij=−β1i=1∑N1=−β1N=1−β=Nπj=i=1∑N−βγij=Ni=1∑Nγij
3. 重复以上的计算,直到对数似然函数不再有明显变化为止。
总结估计GMM参数的EM算法如下:
高斯混合模型(Gaussian Mixture Model,GMM)下的EM算法——举例说明
下面举个例子来说明一下,
已知男生和女生的身高服从高斯分布,其中男生身高服从参数为 ( u 1 , σ 1 2 ) ({u_1},\sigma _1^2) (u1,σ12)的高斯分布,女生身高服从参数为 ( u 2 , σ 2 2 ) ({u_2},\sigma _2^2) (u2,σ22)的高斯分布,现在已知N个样本的观测值为 x 1 , x 2 , ⋯ , x N {x_1},{x_2}, \cdots ,{x_N} x1,x2,⋯,xN,但是不知道这些身高值代表的是男还是女,如果用 π 1 {\pi _1} π1表示这些数据来自高斯分布 N ( u 1 , σ 1 2 ) N({u_1},\sigma _1^2) N(u1,σ12)的概率,用 π 2 {\pi _2} π2表示这些数据来自高斯分布 N ( u 2 , σ 2 2 ) N({u_2},\sigma _2^2) N(u2,σ22)的概率。那么用观测样本来估计参数 θ k = ( π k , u k , σ k 2 ) , k = 1 , 2 {\theta _k} = ({\pi _k},{u_k},\sigma _k^2),k = 1,2 θk=(πk,uk,σk2),k=1,2的值。
那么这其实就是一个一元的高斯混合模型。可采用如下方式来求解。
1.先猜测参数值
男 : u 1 = 1.75 , σ 1 2 = 50 , π 1 = 0.5 女 : u 2 = 1.62 , σ 2 2 = 30 , π 2 = 0.5 \begin{array}{l} 男:{u_1} = 1.75,\sigma _1^2 = 50,{\pi _1} = 0.5\\\\ 女:{u_2} = 1.62,\sigma _2^2 = 30,{\pi _2} = 0.5 \end{array} 男:u1=1.75,σ12=50,π1=0.5女:u2=1.62,σ22=30,π2=0.5
这一步相当于EM算法中的第一步,设置参数的初始值。
2.
2.1假设 x 1 = 1.84 {x_1} = 1.84 x1=1.84,那么使用高斯概率密度函数可以算出 p 1 , p 2 {p_1},{p_2} p1,p2,此时又已知 π 1 , π 2 {\pi _1},{\pi _2} π1,π2(第一步猜测的值),所以,可以算出该样分别属于男生和女生的概率,即,
P ( 1 , 男 ) = p 1 π 1 p 1 π 1 + p 2 π 2 P ( 1 , 女 ) = p 2 π 2 p 1 π 1 + p 2 π 2 \begin{array}{l} P(1,男) = \frac{{{p_1}{\pi _1}}}{{{p_1}{\pi _1} + {p_2}{\pi _2}}}\\\\ P(1,女) = \frac{{{p_2}{\pi _2}}}{{{p_1}{\pi _1} + {p_2}{\pi _2}}} \end{array} P(1,男)=p1π1+p2π2p1π1P(1,女)=p1π1+p2π2p2π2
其实这一步就是EM算法里求 γ i k {\gamma _{ik}} γik,即相当于EM算法中的E步。
这里假设算出来 P ( 1 , 男 ) = 0 . 8 , P ( 1 , 女 ) = 0.2 P(1,男) = {\rm{0}}{\rm{.8,}}P(1,女) = 0.2 P(1,男)=0.8,P(1,女)=0.2。
2.2那么再来算一个值,即 x 1 = 1.84 {x_1} = 1.84 x1=1.84这个样本属于男性和女性的数据
x 1 ( 男 ) = 0 . 8 ∗ 1 . 84 = 1 . 472 x 1 ( 女 ) = 0 . 2 ∗ 1 . 84 = 0 . 368 \begin{array}{l} {x_1}(男) = {\rm{0}}{\rm{.8*1}}{\rm{.84 = 1}}{\rm{.472}}\\\\ {x_1}(女) = {\rm{0}}{\rm{.2*1}}{\rm{.84 = 0}}{\rm{.368}} \end{array} x1(男)=0.8∗1.84=1.472x1(女)=0.2∗1.84=0.368
对于上面结果的解释,可以认为 x 1 = 1.84 {x_1} = 1.84 x1=1.84这个样本其中有1.472的部分属于男性,有0.368的部分属于女性,当然这仅仅是从数学层面上来解释。
2.3 重复上述过程,直到第N个样本,这样就能得到一系列如下的值,
P ( i , 男 ) P ( i , 女 ) , x i ( 男 ) , x i ( 女 ) , i = 1 , 2 , ⋯ , N P(i,男)P(i,女),{x_i}(男),{x_i}(女),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;\;i = 1,2, \cdots ,N P(i,男)P(i,女),xi(男),xi(女),i=1,2,⋯,N
3.更新参数
这里的均值为
u 1 = x 1 ( 男 ) + x 2 ( 男 ) + ⋯ + x N ( 男 ) P ( 1 , 男 ) + P ( 2 , 男 ) + ⋯ + P ( N , 男 ) {u_1} = \frac{{{x_1}(男){\rm{ + }}{x_2}(男){\rm{ + }} \cdots {\rm{ + }}{x_N}(男)}}{{P(1,男) + P(2,男){\rm{ + }} \cdots {\rm{ + }}P(N,男)}} u1=P(1,男)+P(2,男)+⋯+P(N,男)x1(男)+x2(男)+⋯+xN(男) u 2 = x 1 ( 女 ) + x 2 ( 女 ) + ⋯ + x N ( 女 ) P ( 1 , 女 ) + P ( 2 , 女 ) + ⋯ + P ( N , 女 ) {u_2} = \frac{{{x_1}(女){\rm{ + }}{x_2}(女){\rm{ + }} \cdots {\rm{ + }}{x_N}(女)}}{{P(1,女) + P(2,女){\rm{ + }} \cdots {\rm{ + }}P(N,女)}} u2=P(1,女)+P(2,女)+⋯+P(N,女)x1(女)+x2(女)+⋯+xN(女)
方差为,
σ 1 2 = P ( 1 , 男 ) ∑ j = 1 N P ( j , 男 ) ( x 1 − u 1 ) 2 + P ( 2 , 男 ) ∑ j = 1 N P ( j , 男 ) ( x 2 − u 1 ) 2 + ⋯ + P ( N , 男 ) ∑ j = 1 N P ( j , 男 ) ( x N − u 1 ) 2 σ 2 2 = P ( 1 , 女 ) ∑ j = 1 N P ( j , 女 ) ( x 1 − u 2 ) 2 + P ( 2 , 女 ) ∑ j = 1 N P ( j , 女 ) ( x 2 − u 2 ) 2 + ⋯ + P ( N , 女 ) ∑ j = 1 N P ( j , 女 ) ( x N − u 2 ) 2 \begin{array}{l} \sigma _{\rm{1}}^{\rm{2}}{\rm{ = }}\frac{{P({\rm{1,男}})}}{{\sum\limits_{j = 1}^N {P(j,男)} }}{({x_1} - {u_1})^2}{\rm{ + }}\frac{{P({\rm{2,男}})}}{{\sum\limits_{j = 1}^N {P(j,男)} }}{({x_{\rm{2}}} - {u_1})^2}{\rm{ + }} \cdots {\rm{ + }}\frac{{P(N{\rm{,男}})}}{{\sum\limits_{j = 1}^N {P(j,男)} }}{({x_N} - {u_1})^2}\\\\ \sigma _2^{\rm{2}}{\rm{ = }}\frac{{P({\rm{1,女}})}}{{\sum\limits_{j = 1}^N {P(j,女)} }}{({x_1} - {u_{\rm{2}}})^2}{\rm{ + }}\frac{{P({\rm{2,女}})}}{{\sum\limits_{j = 1}^N {P(j,女)} }}{({x_{\rm{2}}} - {u_{\rm{2}}})^2}{\rm{ + }} \cdots {\rm{ + }}\frac{{P(N{\rm{,女}})}}{{\sum\limits_{j = 1}^N {P(j,女)} }}{({x_N} - {u_{\rm{2}}})^2} \end{array} σ12=j=1∑NP(j,男)P(1,男)(x1−u1)2+j=1∑NP(j,男)P(2,男)(x2−u1)2+⋯+j=1∑NP(j,男)P(N,男)(xN−u1)2σ22=j=1∑NP(j,女)P(1,女)(x1−u2)2+j=1∑NP(j,女)P(2,女)(x2−u2)2+⋯+j=1∑NP(j,女)P(N,女)(xN−u2)2
混合系数为,
π 1 = ∑ i = 1 N P ( i , 男 ) ∑ i = 1 N P ( i , 男 ) + ∑ i = 1 N P ( i , 女 ) = ∑ i = 1 N P ( i , 男 ) N π 2 = ∑ i = 1 N P ( i , 女 ) ∑ i = 1 N P ( i , 男 ) + ∑ i = 1 N P ( i , 女 ) = ∑ i = 1 N P ( i , 女 ) N \begin{array}{l} {\pi _{\rm{1}}}{\rm{ = }}\frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} }}{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} + \sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }} = \frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} }}{N}\\\\ {\pi _2}{\rm{ = }}\frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }}{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} + \sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }} = \frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }}{N} \end{array} π1=i=1∑NP(i,男)+i=1∑NP(i,女)i=1∑NP(i,男)=Ni=1∑NP(i,男)π2=i=1∑NP(i,男)+i=1∑NP(i,女)i=1∑NP(i,女)=Ni=1∑NP(i,女)
这一步其实就是EM算法中的M步,参数更新式。