机器学习基础03-概率论与数理统计
文章目录
- 概率论基础
- 概率论基础要点
- 随机试验
- 样本空间与样本点
- 随机事件
- 事件的性质与运算
- 频率与概率
- 频率学派和贝叶斯学派?
- 概率的性质
- 古典概型
- 几何概型
- 条件概率
- 条件概率
- 加法公式
- 乘法公式
- 排列组合
- 全概率公式
- 概率分布
- 要点
- 离散型分布与连续型分布
- 伯努利分布(又叫两点分布或01分布)
- 二项分布
- 数学期望
- 期望的性质
概率论基础
概率论基础要点
-
概率论基础概念
-
事件与概率
-
古典概型与几何概型
-
确定性现象:条件完全决定结果
-
随机性现象:条件不能完全决定结果,在一定条件下,可能出现这样的结果,也可能出现那样的结果,我们预先无法断言,这类现象称为随机现象
-
概率论与数理统计是研究什么的?
- 随机现象:不确定性与统计规律性
- 概率论:从数量上研究随机现象的统计规律性的科学
- 数理统计:从应用角度研究处理随机性数据,建立有效的统计方法,进行统计推理
随机试验
定义1:概率论中,将具有以下三个特点的试验称为随机试验,简称试验。随机试验常用 E E E表示。
- 在相同的情况下试验可以多次重复进行
- 一次试验结果不止一个,且试验之前无法确定具体是哪种结果
- 全部试验结果预先是确定的,且每次试验有且仅有一个结果出现
例如: E 1 E_1 E1抛一枚硬币,观察正面 H H H、反面 T T T出现的情况
E 2 E_2 E2掷一颗骰子,观察出现的点数
都是随机试验
样本空间与样本点
定义2 样本空间:试验的所有结果所组成的集合称为试验 E E E的样本空间,记为 Ω \Omega Ω。
试验的每个可能的结果(样本空间中的元素)称为试验 E E E的一个样本点
例如:
E 1 E_1 E1:抛一枚硬币,观察正面 H H H、反面 T T T出现的情况; Ω 1 = { H , T } \Omega_1=\{H,T\} Ω1={H,T};
E 2 E_2 E2:掷一颗骰子,观察出现的点数; Ω 2 = { 1 , 2 , 3 , 4 , 5 , 6 } \Omega_2=\{1,2,3,4,5,6\} Ω2={1,2,3,4,5,6};
随机事件
定义3 随机事件样本空间的任意一个子集称为随机事件,简称“事件”,记作 A , B , C A,B,C A,B,C等。
例如在试验 E 2 E_2 E2中,令 A A A表示“出现奇数点”, A A A就是一个随机事件。
A A A还可以用样本点的集合形式表示 ,即 A = { 1 , 3 , 5 } A=\{1,3,5\} A={1,3,5},它是样本空间 Ω \Omega Ω的一个子集
基本事件: 随机事件仅包含一个样本点 ω \omega ω,单点子集 { ω } \{\omega\} {ω}。
复合事件: 包含两个或两个以上样本点的事件。
事件的性质与运算
(随机)事件的材质就是集合,集合的一切性质和运算都适用于事件
频率与概率
定义4 在相同的条件下,进行了 n n n次试验,在这 n n n次试验中,事件 A A A发生的次数 n A n_A nA称为事件 A A A发生的频数。比值 n A n \frac{n_A}{n} nnA称为事件发生的频率,并记为 f n ( A ) f_n(A) fn(A)
在相同的条件下进行 n n n次重复试验,当 n n n趋于无穷大时,事件 A A A发生的频率 f n ( A ) f_n(A) fn(A)稳定于某个确定的常数 p p p,称此常数 p p p为事件 A A A发生的概率,记作 P ( A ) = p P(A)=p P(A)=p
频率学派和贝叶斯学派?
概率的性质
- 0 ≤ P ( A ) ≤ 1 , P ( ∅ ) = 0 0\le{P}(A)\le{1}, P(\varnothing)=0 0≤P(A)≤1,P(∅)=0
- 互补性: P ( A ˉ ) = 1 − P ( A ) P(\bar{A})=1-P(A) P(Aˉ)=1−P(A)
- P ( A − B ) = P ( A ) − P ( A B ) P(A-B)=P(A)-P(AB) P(A−B)=P(A)−P(AB)
- 加法公式:对于任意事件A,B,有 P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) P(A+B)=P(A)+P(B)-P(AB) P(A+B)=P(A)+P(B)−P(AB)
例:设 A , B A,B A,B为两个随机事件, P ( A ) = 0.5 , P ( A ∪ B ) = 0.8 , P ( A B ) = 0.3 , 求 P ( B ) P(A)=0.5, P(A\cup{B})=0.8,P(AB)=0.3,求P(B) P(A)=0.5,P(A∪B)=0.8,P(AB)=0.3,求P(B)
因为: P ( A ∪ B ) P(A\cup{B}) P(A∪B)=P(A)+P(B)-P(AB)
得 P ( B ) = P ( A ∪ B ) − P ( A ) + P ( A B ) = 0.8 − 0.5 + 0.3 = 0.6 P(B)=P(A\cup{B})-P(A)+P(AB)=0.8-0.5+0.3=0.6 P(B)=P(A∪B)−P(A)+P(AB)=0.8−0.5+0.3=0.6
古典概型
定义5:理论上,具有下面两个特点的随机试验的概率模型,称为古典概型(或等可能概型):
1、有限性:基本事件是总数是有限的,换句话说样本空间仅包含有限个样本点
2、等可能性:每个基本事件发生的可能性是相同的。
古典概型的概率计算公式:
设事件 A A A中所含的样本点个数为 r r r,样本空间 Ω \Omega Ω中样本点总数为 n n n,则有
P ( A ) = r n = A 中 样 本 点 数 Ω 中 样 本 点 总 数 P(A)=\frac{r}{n}=\frac{A中样本点数}{\Omega中样本点总数} P(A)=nr=Ω中样本点总数A中样本点数
P ( A ) = r n = A 所 包 含 的 基 本 事 件 数 基 本 事 件 总 数 P(A)=\frac{r}{n}=\frac{A所包含的基本事件数}{基本事件总数} P(A)=nr=基本事件总数A所包含的基本事件数
例2:从1-9个数字中有放回的抽取两次,这两次数字相同的概率是多少?
完备事件组= { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } \{1,2,3,4,5,6,7,8,9\} {1,2,3,4,5,6,7,8,9}
P ( 两 次 数 字 一 样 ) P(两次数字一样) P(两次数字一样)=1- P ( 两 次 数 字 不 一 样 ) P(两次数字不一样) P(两次数字不一样)
第一次是任意抽取,第二次是在不包括第一次的数中取数即可,因此 r 1 = 9 , r 2 = 8 r_1=9,r_2=8 r1=9,r2=8
P ( A ) = 8 ∗ 9 9 ∗ 9 = 8 9 P(A)=\frac{8*9}{9*9}=\frac{8}{9} P(A)=9∗98∗9=98
几何概型
把有限个样本点推广到无限个样本点的场合,人们引入了几何概型,由此形成了确定概率的另一方法-几何方法
定义6:若对于一随机试验,每个样本点出现是等可能的,样本空间 Ω \Omega Ω所含的样本点个数为无穷多个,且具有非零的,有限的几何度量,即 0 < m ( Ω ) < ∞ 0<m(\Omega)<\infty 0<m(Ω)<∞,则称这一随机试验是一几何概型。
当随机试验的样本空间是某个区域,并且任意一点落在度量(长度、面积、体积)相同的子区域是等可能的,则事件 A A A的概率可定义为
P ( A ) = m ( A ) m ( Ω ) P(A)=\frac{m(A)}{m(\Omega)} P(A)=m(Ω)m(A)
其中, m ( Ω ) m(\Omega) m(Ω)是样本空间的度量, m ( A ) m(A) m(A)是构成事件 A A A的子区域的度量,这样借助于几何上的度量来合理规定的概率称为几何概率
条件概率
条件概率
概率加法公式:若事件 A A A与 B B B互斥,则 P ( A ∪ B ) = P ( A ) + P ( B ) P(A\cup{B})=P(A)+P(B) P(A∪B)=P(A)+P(B),那么怎么求 A A A与 B B B的积事件 A B AB AB呢?
note:
- 事件 A A A发生对事件 B B B发生的概率没有影响,则称两事件是相互独立的
- 事件 A A A与 B B B至少有一个发生的事件叫 A A A与 B B B的和事件,记为 A ∪ B A\cup{B} A∪B或 A + B A+B A+B
- 事件 A A A与 B B B都发生的事件叫做 A A A与 B B B的积事件,记为 A ∩ B 或 A B A\cap{B}或AB A∩B或AB
- 若 A B AB AB是不可能事件,则说事件 A A A与 B B B互斥
条件概率:一般地,设 A A A, B B B为两个事件,且 P ( A ) > 0 P(A)>0 P(A)>0,称:
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
为在事件 A A A发生的条件下,事件 B B B发生的条件概率 P ( B ∣ A ) P(B|A) P(B∣A)
读作: A A A发生的条件下 B B B的概率
在 A A A事件已经发生的情况下, P ( B ∣ A ) P(B|A) P(B∣A)相当于是 A = Ω A=\Omega A=Ω的。,因此
P ( B ∣ A ) = P ( A B ) P ( A ) ( P ( A ∩ B = P ( A B ) Ω ) ) P(B|A)=\frac{P(AB)}{P(A)}(P(A\cap{B}=\frac{P(AB)}{\Omega})) P(B∣A)=P(A)P(AB)(P(A∩B=ΩP(AB)))
分子 P ( A ∩ B ) = P ( A B ) P(A\cap{B})=P(AB) P(A∩B)=P(AB),仍然是下图中深蓝色的部分,面积不变。因为 A A A事件确定已经发生,因此分母 Ω \Omega Ω变成了 P ( A ) P(A) P(A)
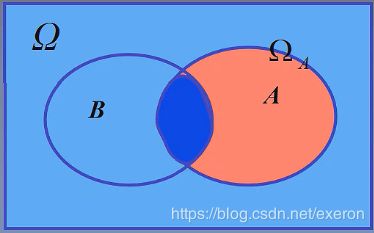
- 0 ≤ P ( B ∣ A ) ≤ 1 0\le{P(B|A)}\le{1} 0≤P(B∣A)≤1
- 几何解释见上图
- 可加性:如果 B 和 C B和C B和C互斥,那么 P [ ( B ∪ C ) ∣ A ] = P ( B ∣ A ) + P ( C ∣ A ) P[(B\cup{C})|A]=P(B|A)+P(C|A) P[(B∪C)∣A]=P(B∣A)+P(C∣A)
加法公式
对于事件空间 Ω \Omega Ω,事件 A A A和 B B B的加法公式是 P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) P(A\cup{B})=P(A)+P(B)-P(A\cap{B}) P(A∪B)=P(A)+P(B)−P(A∩B),若 A , B A,B A,B事件相互独立,那么: P ( A ∩ B ) = 0 P(A\cap{B})=0 P(A∩B)=0
例:设 A , B A,B A,B为两个随机事件, P ( A ) = 0.6 , P ( B ) = 0.4 , P ( A B ) = 0.3 P(A)=0.6, P(B)=0.4, P(AB)=0.3 P(A)=0.6,P(B)=0.4,P(AB)=0.3,求 P ( A ∪ B ) P(A\cup{B}) P(A∪B)。若 A , B A,B A,B相互独立,求 P ( A ∪ B ) P(A\cup{B}) P(A∪B)
0.6+0.4-0.3=0.7
1
乘法公式
若 P ( B ) > 0 P(B)>0 P(B)>0,
- P ( B ∣ A ) P ( A ) = P ( A B ) P(B|A)P(A)=P(AB) P(B∣A)P(A)=P(AB)
- P ( A ∣ B ) P ( B ) = P ( A B ) P(A|B)P(B)=P(AB) P(A∣B)P(B)=P(AB)
上式称为条件事件的乘法公式
若 A , B A,B A,B事件相互独立,那么: P ( A B ) = P ( A ) P ( B ) = 0 ? ? ? P(AB)=P(A)P(B)=0??? P(AB)=P(A)P(B)=0???
上式可能推广到 A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An个独立事件,且 P ( A 1 A 2 . . . A n ) > 0 P(A_1A_2...A_n)>0 P(A1A2...An)>0,则 P ( A 1 A 2 . . . A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) . . . P ( A n ∣ A 1 A 2 . . . A n − 1 ) P(A_1A_2...A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_n|A_1A_2...A_{n-1}) P(A1A2...An)=P(A1)P(A2∣A1)P(A3∣A1A2)...P(An∣A1A2...An−1)
上式就是条件概率下的链式法则
排列组合
组合:从n个元素中抽取m个元素组成一组:(不考虑其顺序)的组合方式个数,记 C n m C_n^m Cnm
C n m = A n m A m m = n ! m ! ( n − m ) ! , 其 中 C n 0 = 1 C_n^m=\frac{A_n^m}{A_m^m}=\frac{n!}{m!(n-m)!},其中C_n^0=1 Cnm=AmmAnm=m!(n−m)!n!,其中Cn0=1
排列:从n个元素中抽取m个元素的所有不同的排列数,记作 A n m , 其 中 m ≤ n A_n^m,其中m\le{n} Anm,其中m≤n
A n m = n ( n − 1 ) . . . ( n − m − 1 ) A_n^m=n(n-1)...(n-m-1) Anm=n(n−1)...(n−m−1)
例:求 C 4 2 和 A 5 2 C_4^2和A_5^2 C42和A52
全概率公式
当求某一事件 A A A的概率比较困难,而求条件概率比较容易时,可先设法将这个事件 A A A分成几个互不相容事件的和,再利用加法公式和乘法公式解之。
定义3,样本 B 1 , B 2 … B n B_1,B_2…B_n B1,B2…Bn为一系列互不相容的事件,且
⋃ i = 1 n B i = Ω \bigcup_{i=1}^nB_i=\Omega i=1⋃nBi=Ω
则对任一事件 A A A,有 P ( A ) = P ( B 1 ) P ( A ∣ B 1 ) + P ( B 2 ) P ( A ∣ B 2 ) + . . . + P ( B n ) P ( A ∣ B n ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+...+P(B_n)P(A|B_n)=\sum_{i=1}^nP(B_i)P(A|B_i) P(A)=P(B1)P(A∣B1)+P(B2)P(A∣B2)+...+P(Bn)P(A∣Bn)=i=1∑nP(Bi)P(A∣Bi)
例1,某工厂有3个车间生产同一种产品,根据以往的记录有以下数据:请问现从出厂产品中任取一件,问取到次品的概率?
| 车间 | 次品率 | 提供份额 |
|---|---|---|
| 1 | 0.02 | 30% |
| 2 | 0.01 | 55% |
| 3 | 0.03 | 15% |
由题意可知,取到次品分别是3个车间的3种不同的概率是互不相容事件。
设取到次品的概率为 A A A,次品是1车间的概率为 A B 1 AB_1 AB1,次品是2车间的概率为 A B 2 AB_2 AB2,次品是3车间的概率为 A B 3 AB_3 AB3,有 A = A B 1 + A B 2 + A B 3 A=AB_1+AB_2+AB_3 A=AB1+AB2+AB3
P ( A ) = P ( A B 1 ) + P ( A B 2 ) + P ( A B 3 ) P(A)=P(AB_1)+P(AB_2)+P(AB_3) P(A)=P(AB1)+P(AB2)+P(AB3)
= P ( B 1 ) P ( A ∣ B 1 ) + P ( B 2 ) P ( A ∣ B 2 ) + P ( B 3 ) P ( A ∣ B 3 ) =P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+P(B_3)P(A|B_3) =P(B1)P(A∣B1)+P(B2)P(A∣B2)+P(B3)P(A∣B3)
= 0.30 ∗ 0.02 + 0.55 ∗ 0.01 + 0.15 ∗ 0.03 = 0.016 =0.30*0.02+0.55*0.01+0.15*0.03=0.016 =0.30∗0.02+0.55∗0.01+0.15∗0.03=0.016

概率分布
要点
- 概率分布类型(离散型分布与连续型分布)
- 期望与方差(概念与计算方法)
- 高斯分布(最常用的连续型分布)
离散型分布与连续型分布
离散型分布:变量只能取离散值,即有限可列举的值;表达形式是分布列或语言描述
连续型分布:变量取一个或多个区间,不可列举;表达形式是函数表达式:概率密度函数
伯努利分布(又叫两点分布或01分布)
如果随机变量只有0和1两种可能的取值,并且相应的概率为:
P ( X = 1 ) = p , P ( X = 0 ) = 1 − p P(X=1)=p, P(X=0)=1-p P(X=1)=p,P(X=0)=1−p
则称随机变量 X X X服从参数为 p p p的伯努利分布。
二项分布
二项分布又叫 n n n重伯努利试验(白努力试验), X X X的取值为 0 , 1 , . . . , n 0,1,...,n 0,1,...,n。因为白努力试验的结果是0或1,设一次白努力试验结果为1的概率为 p p p,则 n n n次白努力试验之后,结果中有 k 个 1 k个1 k个1的概率为:
P ( X = k ) = C n k p k ( 1 − p ) n − k , k = 0 , 1 , . . . , n P(X=k)=C_n^kp^k(1-p)^{n-k},k=0,1,...,n P(X=k)=Cnkpk(1−p)n−k,k=0,1,...,n
例:临床上用针灸治疗某种头痛,有效的概率为60%,现用该方法治疗3个病例,其中两例有效的概率是多少?
C 3 2 ∗ 0. 6 2 ∗ 0. 4 1 = 3 ∗ 0.36 ∗ 0.4 = 0.432 C_3^2*0.6^2*0.4^1=3*0.36*0.4=0.432 C32∗0.62∗0.41=3∗0.36∗0.4=0.432
再例:扔硬币10次都向上的概率是?
C 10 10 ∗ 0. 5 10 ∗ 0. 5 0 = ( 1 2 ) 10 = 1 1024 = 0.0009765625 C_{10}^{10}*0.5^{10}*0.5^{0}=(\frac{1}{2})^{10}=\frac{1}{1024}=0.0009765625 C1010∗0.510∗0.50=(21)10=10241=0.0009765625
10次中6次向上的概率是?
C 10 6 ∗ 0. 5 6 ∗ 0. 5 4 = 210 ∗ 1 64 ∗ 1 16 = C_{10}^6*0.5^6*0.5^4=210*\frac{1}{64}*\frac{1}{16}= C106∗0.56∗0.54=210∗641∗161=
数学期望
期望的性质
E ( C ) = C E(C)=C E(C)=C
E ( a X ) = a E ( X ) E(aX)=aE(X) E(aX)=aE(X)
E ( X + Y ) = E ( X ) + E ( Y ) E(X+Y)=E(X)+E(Y) E(X+Y)=E(X)+E(Y)
当 X Y XY XY相互独立时, E ( X Y ) = E ( X ) E ( Y ) E(XY)=E(X)E(Y) E(XY)=E(X)E(Y)