哈夫曼树及哈夫曼编码
哈夫曼树
哈夫曼树,最优二叉树,带权路径长度(WPL)最短的树。它没有度为1的点,是一棵严格的二叉树(满二叉树)。
何谓‘带权路径长度’
了解哈夫曼树,我们首先要知道树的几个相关术语,并了解什么是WPL。
- 路径:从树中一个结点到另一个结点之间的分支构成两个结点之间的路径
- 路径长度:路径上的分支数目
- 树的路径长度:从树根到每一个结点的路径长度之和
- 树的带权路径长度:树中所有叶子结点的带权路径之和 W P L = ∑ k = 1 n w k l k WPL=\sum_{k=1}^n{w_kl_k} WPL=∑k=1nwklk,其中 w k w_k wk为第k个结点的权值
- 最优二叉树(哈夫曼树):WPL最小的二叉树
注:树的WPL这个概念非常重要,这个公式直接产生了哈夫曼编码数据压缩的应用
哈夫曼算法
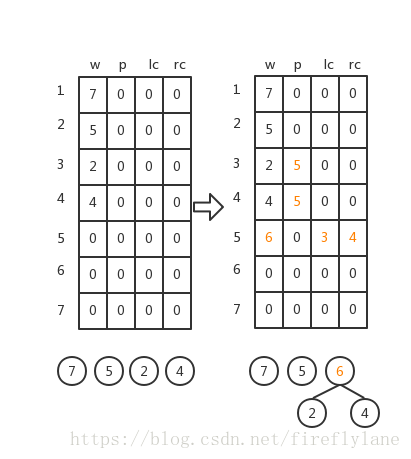
- 根据给定的n个权值{ w 1 w_1 w1, w 2 w_2 w2,···, w n w_n wn}构成n棵二叉树的集合F={ T 1 T_1 T1, T 2 T_2 T2,···, T n T_n Tn},其中每棵二叉树 T i T_i Ti中只有一个带权为 w i w_i wi的根结点,其左右子树均空
- 在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左。右子树上根结点的权值之和。
- 在F中删除这两棵树,同时将新得到的二叉树加入F中。
- 重复(2)(3),直到F只含一棵树为止。这棵树即为哈夫曼树
哈夫曼编码
在谈论哈夫曼编码之前,我们先来了解一下编码的相关概念。
等长的二进制编码
对于一个无记忆离散信源中每一个符号,若采用相同长度的不同码字代表相应的符号,就称为等长编码。如:A/B/C/D采用00/01/10/11编码就是一个等长的编码。
不等长的二进制编码
在数据传输过程中,我们需要压缩文件,就可以通过不等长编码的方式。
哈夫曼编码就是一种不等长的编码,它根据字频分析结果决定每个字符的编码长度,出现概率高的字符编码短,出现概率低的编码长。哈夫曼研究这种最优树的目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题。
但是文件压缩了之后我们需要解压才能得到想要的文件,编码了之后我们还需解码。下面我们来看一下一个不等长编码的二进制编码的示例:同样我们给对A/B/C/D编码,分别为0/00/1/01,很容易看出如果我们收到电文0000,我们则无法得到唯一的译文(0000可以翻译成AAAA、BB等等)
一般来说,若要实现无失真的编码,这不但要求信源符号与码字是一一对应的,而且要求码符号序列的反变换也是唯一的。也就是说,一个码的任意一串有限长的码符号序列(码字)只能被唯一地翻译成所对应的信源符号序列。不然我们的译文就会有二义性,这样的编码是没有意义的。
为了解决不等长二进制编码译码的二义性问题,我们需要引入一个概念前缀码
前缀码是一种不等长的编码,它保证任何一个字符的编码都不是另一个编码的前缀。比如A(0),B(10),C(110),D(1111)就是一组前缀码。
哈夫曼树构造哈夫曼编码
在编写一个具体的算法之前,我们总要先思考算法的载体——数据如何被存储。哈夫曼算法的关键数据结构为哈夫曼树,所以接下来我们来思考哈夫曼树的存储。
哈夫曼树的存储
我们采用孩子双亲表示法存储哈夫曼树
typedef struct{
unsigned int weight;
unsigned int parent, lchild, rchild;
} HTNode, *HuffmanTree; //动态分配数组存储哈夫曼树
定义一个char型二级指针存储哈夫曼编码
typedef char **HuffmanCode;
哈夫曼树的构造
哈夫曼树的构造思想就是利用二叉树的非叶子结点来实现二叉树的结构(:我在说什么
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n)
{
if(n<=1) return;
// 初始化哈夫曼树
m = 2*n-1;
HT = (HuffmanTree)malloc((m+1)*sizeof(HTNode));
HuffmanTree p;
int i;
for(p = HT, i = 1; i <= n; ++i, ++p, ++w) *p = {*w, 0, 0, 0};
for(; i <= m; ++i; ++p) *p = {0, 0, 0, 0};
// 构造哈夫曼树
for(i = n+1; i <= m; ++i)
{
select(HT, i-1, s1, s2); //选择parent为0且权值最小的两个结点s1,s2
HT[s1].parent = i; HT[s2].parent = i;
HT[i].lchild = s1; HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s1].weight;
}
}
下面对这段代码的一些细节略加解释:
- 传参时使用引用实现了直接对函数外变量的修改,解决了C函数按值传递且只有单返回值的弊端
- *w表示待编码的字符数组,n表示字符个数,m=2n-1表示哈夫曼树的结点个数,至于
分配m+1个结点的空间,则是为了将结点标号和数组下标对应起来,数组的0号元素弃置不用(树的常见存储) - malloc函数的返回值为void*,需要将其强转成HTNode的指针,即HuffmanTree类型
HuffmanTree p是为遍历并初始化动态分配的内存块而设的HTNode指针,int i是为了循环而设的辅助变量
哈夫曼编码
以下代码依据从叶子到根逆向求每个字符的哈夫曼编码
// 哈夫曼编码
HC = (HuffmanCode)malloc((n+1)*sizeof(char *));
cd = (char*)malloc(n*sizeof(char));
cd[n-1] = "\0";
for(int i = 1; i <= n; ++i)
{
start = n-1;
for(int c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
if(HT[f].lchild == c) cd[--start] = "0";
else cd[--start] = "1";
HC[i] = (char*)malloc((n-start)*sizeof(char));
strcpy(HC[i], &cd[start]);
}
free(cd);
注记:
- 同理,开辟 n+1个char* 的空间为了将数组下标i与第i个待编码的字符对应起来
- cd为辅助数组,用于给单个字符编码,由于一开始不知道每个字符的编码长度,所以使用cd开足够大的编码空间n,最后将编码完成后就将确定长度的编码串拷贝到
哈夫曼表HC中
最后献上Huffman编码算法的完整代码
typedef struct{
unsigned int weight;
unsigned int parent, lchild, rchild;
} HTNode, *HuffmanTree; //哈夫曼树结点和根结点
typedef char **HuffmanCode; //哈夫曼编码表
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n)
{
if(n<=1) return;
// 初始化哈夫曼树
m = 2*n-1;
HT = (HuffmanTree)malloc((m+1)*sizeof(HTNode));
HuffmanTree p;
int i;
for(p = HT, i = 1; i <= n; ++i, ++p, ++w) *p = {*w, 0, 0, 0};
for(; i <= m; ++i; ++p) *p = {0, 0, 0, 0};
// 构造哈夫曼树
for(i = n+1; i <= m; ++i)
{
select(HT, i-1, s1, s2); //选择parent为0且权值最小的两个结点s1,s2
HT[s1].parent = i; HT[s2].parent = i;
HT[i].lchild = s1; HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s1].weight;
}
// 哈夫曼编码
HC = (HuffmanCode)malloc((n+1)*sizeof(char *));
cd = (char*)malloc(n*sizeof(char));
cd[n-1] = "\0";
for(int i = 1; i <= n; ++i)
{
start = n-1;
for(int c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
if(HT[f].lchild == c) cd[--start] = "0";
else cd[--start] = "1";
HC[i] = (char*)malloc((n-start)*sizeof(char));
strcpy(HC[i], &cd[start]);
}
free(cd);
}
习题
例1 电文的译码:分解电文中字符串,从根结点出发,按字符0/1确定左、右孩子,直到叶子结点。
char text[maxn] = "101110110111";
for(int i = 0; i < text.length(); i++)
{
HuffmanTree p; // 辅助变量指向哈夫曼树首地址
HuffmanCoding(p, HC, text, text.length()); //HC为哈夫曼编码表
p += text.length(); // 将指针指向哈夫曼树头结点
while(p->lchild || p->rchild)
{
if(text[i] == 0) p = p->lchild;
else p = p->rchild;
j += 1;
}
}
例2 已知某系统在通信联络中只可能出现8种字符,其概率分布为0.05, 0.29, 0.07, 0.08, 0.14, 0.23, 0.03, 0.11, 试设计哈夫曼编码。
分析:首先设8个字符的权分别为w={5, 29, 7, 8, 14, 23, 3, 11}, n = 8, 则m = 15, 即在有8个叶子结点的哈夫曼树上有15个结点,然后构造一棵哈夫曼树,最后就得到哈夫曼编码。
哈夫曼树的应用场景
其实哈夫曼树使用场景还真不少,例如apache负载均衡的按权重请求策略的底层算法、咱们生活中的路由器的路由算法、利用哈夫曼树实现汉字点阵字形的压缩存储、快速检索信息等等底层优化算法,其实核心就是因为目标带有权重、长度远近这类信息才能构建赫夫曼模型。
ps:哈夫曼树最优子结构性质的证明可以详见这篇博文算法学习之哈夫曼编码算法