如何以最快的速度计算出一个二进制数中1的个数

题目：如何以最快的速度计算出一个二进制数中1的个数
重点在于，这里有十亿或万亿个int数字，怎样做才能优化算法呢？

解答：

统计一个字节序列中1的个数，我首先想到的是最简单，把这个数每次右移一位，然后与0x01逻辑与进行统计，相当于总共将真个字节序列遍历了一遍。然而仔细想想，一个十亿或万亿的字节序列，能存到一个数（或称为变量）中？必然不可以，因此这是陷阱所在。

while(num)
{
    if(num & (0x1 ) == 0x1)
    { 
        count ++; 
        num >>= 1;
    }
}

深入思考，既然是字节序列，那我解释成任何数据类型都是可以的啊，我可以按照32位机器的int大小，比如4个字节来把这么长的字节序列读到一个个的Int值中，然后统计每个int值的位中1的个数，加起来就可以了。

方法1：

    8bit静态表查找法 Precompute_8bit

    static int bits_in_char [256] = {             

    0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2,

    3, 3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3,

    3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3,

    4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4,

    3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5,

    6, 6, 7, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4,

    4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5,

    6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 2, 3, 3, 4, 3, 4, 4, 5,

    3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 3,

    4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 4, 5, 5, 6, 5, 6, 6, 7, 5, 6,

    6, 7, 6, 7, 7, 8

    };

    int bitcount (unsigned int n)

    {

        // works only for 32-bit ints

        return bits_in_char [n & 0xffu]

             + bits_in_char [(n >>8) & 0xffu]

             + bits_in_char [(n >> 16) & 0xffu]

             + bits_in_char [(n >> 24) & 0xffu] ;

     }

    使用静态数组表，列出所有8bit(256个)无符号数含有Bit1的个数。将32Bit 的n分4部分，直接在表中找到对应的Bit1的个数，然后求和。

    显然，牺牲了时间换取了空间。

方法2：

//源自 微软 的一道面试题

int GetNumOfOne(int x)
{
    int count = 0;
    while (x)
    {
        count++;
        x = x & (x - 1);
    }
    return count;
}
//原理：一个数减去1，则这个数的二进制数中最后一个1及其后的数字取反。
//     x & (x - 1) 为它的二进制数中少一个1

方法3：
//以32位为例子:
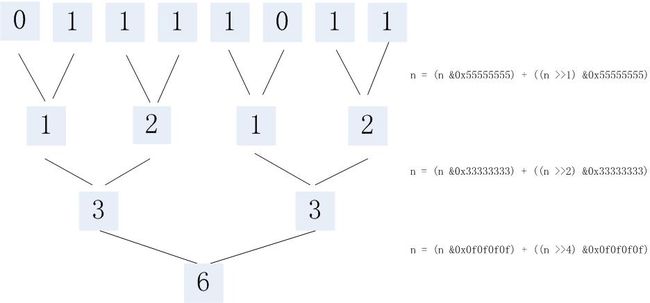
//将n写成二进制形式，然后相邻位相加，重复这个过程，直到只剩下一位。以123为例，二进制为1111101，如下图：
void find32One(int n) 
{

        const int MASK1 = 0x55555555;
        const int MASK2 = 0x33333333;
        const int MASK4 = 0x0f0f0f0f;
        const int MASK8 = 0x00ff00ff;
        const int MASK16 = 0x0000ffff;

        n = (n & MASK1) + ((n >> 1) & MASK1);
        n = (n & MASK2) + ((n >> 2) & MASK2);
        n = (n & MASK4) + ((n >> 4) & MASK4);
        n = (n & MASK8) + ((n >> 8) & MASK8);
        n = (n & MASK16) + ((n >> 16) & MASK16);

        cout << n << " number of 1." << endl;
}

//图解：