【Think Python】Python笔记(二十一)算法分析
算法分析的实际目的是分析预测不同算法的性能,用于指导设计决策;
- 有时候算法分析面临一些问题:
- 算法的性能依赖于硬件的特性:指定一个机器模型并分析一个算法在一个给定的模型下所需的步骤或者运算的数目;
- 相对性能可能依赖于数据集的细节:分析最坏情况;
- 相对性能依赖于问题的规模:将运行时将表示成问题规模的函数;
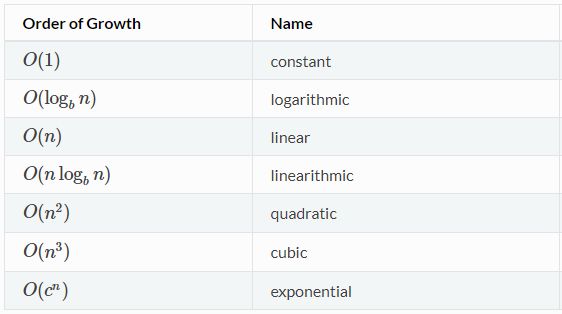
(一)增长量级
**首项:**最高指数的项;一般来说具有较小首项的算法对于规模比较大的问题是好的算法;
通常来讲,具有相同首项的算法被认为是相当的;
下面的算法的增量级从低到高:
-
对于对数来讲,对数的基数并不影响增量级,改变基数等价于乘以一个常数
-
虽然我们通常使用增量级来描述算法的性能,但是:
- 有时候系数和非首选项产生巨大的影响
- 有时候硬件的细节、编程语言、输入的特性会造成巨大的影响
(二)python基本运算操作分析
- python中大部分算数运算的开销是常数级的;乘法比加减法用更长的时间,除法则会更长;
- 索引操作——在序列中或者字典中读写元素的增量级是常数级的;
- 一层循环是线性的,嵌套的循环增量级要相乘;
- 大部分字符串和元组运算是线性的,除了索引和
len;- 切片运算与输出的长度成正比,但是和输入的大小无关;
- 所有的字符串方法都是线性的,比如
join;
大部分列表操作是线性的,例外:
- 列表尾部增加元素是常数级;
- 结尾删除元素是常数级
- 排序是O(nlogn);
大部分租店运算和方法是常数时间,例外:
update的运算时间与作为形参被传递的字典大小成正比;
keys,values,items是常数级的时间,因为返回迭代器;
(三)搜索算法分析
搜索 (search)算法,接受一个集合以及一个目标项,并判断该目标项是否在集合中,通常返回目标的索引值;
- 序列的
in操作符使用的是线性搜索,即顺序查找; - 字符串中
find和count方法使用的也是线性搜索;
如果是已经排序好的序列,可以使用二分查找,时间复杂度是O(logn);
另一个检索速度非常快的数据结构是哈希表(hashtable)
- 可以在常数的时间内检索结果,并不依赖于序列是不是已经排序;
- python中的字典是采用的哈希表技术实现的;因此大多数字典操作时间复杂度都是常数级的;
(四)哈希表
下面的过程用python说明哈希表的实现过程:
- 首先必须实现的两个操作:
add(k, v)增加新项;get(k)查找并返回值;
使用元组列表:
class LinearMap:
def __init__(self):
self.items = []
def add(self, k, v):
self.items.append((k, v))
def get(self, k):
for key, val in self.items:
if key == k:
return val
raise KeyError
上面的查找是顺序查找,另外的方案是将列表按照键值进行排序,使用二分查找,时间复杂度是对数级,但是添加一个元素是线性的;
- 另一种解决方案是将键值对列表分成小列表:
class BetterMap:
def __init__(self, n=100):
self.maps = []
for i in range(n):
self.maps.append(LinearMap())
def find_map(self, k):
index = hash(k) % len(self.maps)
return self.maps[index]
def add(self, k, v):
m = self.find_map(k)
m.add(k, v)
def get(self, k):
m = self.find_map(k)
return m.get(k)
__init__会生成一个由 n 个 LinearMap 组成的列表;find_map使用内建函数hash,这个内建函数接受几乎所有的python对象并返回一个整数【被认为相等的可哈希对象对应相同的哈希值】;
- **使得哈希表变快的关键:**如果能保证
LiearMap的最大长度是有上限的,则LinearMap.get的时间复杂度的增长量级是常数的;这样跟踪每个LinearMap的项数,当超过某个阈值的时候,增加更多的LinearMap来调整哈希表的大小:
class HashMap:
def __init__(self):
self.maps = BetterMap(2)
self.num = 0 //用于跟踪项的数量
def get(self, k):
return self.maps.get(k)
def add(self, k, v):
if self.num == len(self.maps.maps):
self.resize()
self.maps.add(k, v)
self.num += 1
def resize(self):
new_maps = BetterMap(self.num * 2)
for m in self.maps.maps:
for k, v in m.items:
new_maps.add(k, v)
self.maps = new_maps
resize生成一个新的BetterMap,是之前的两倍大,之后从旧表重新"哈希"到新的表【重新哈希是必要的的,因为哈希表变大以后,其中每个键对应的哈希值会变化】
- 这个算法的一个特性是,当我们调整
HashTable大小的时候,是几何式增长