遗传算法解决八皇后问题（java源码）

本文源码下载链接：https://download.csdn.net/download/goulvjiang3176/11221063
另有贪心算法解决八皇后问题的源码下载链接：https://download.csdn.net/download/goulvjiang3176/11221066
以及深度优先和广度优先遍历解决八皇后问题源码下载链接：https://download.csdn.net/download/goulvjiang3176/11219489
由于上述两种方法比较容易实现，就不赘述了，本文详细介绍遗传算法解决八皇后问题的解决方案

1. N皇后问题描述

N皇后问题描述如下：在n×n格棋盘上放置彼此不互相攻击的N个皇后。按国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。N皇后问题等价于在以下三个约束条件：任何2个皇后不放在同一行；任何2个皇后不放在同一列；任何2个皇后不放在同斜线。
我们把n×n的棋盘看作二维方阵，其行号从上到下列号从左到右依次编号为0，1，…，7。设任意两个皇后，皇后1和皇后2的坐标分别是（i，j）和（k，l），则如果这两个皇后在从棋盘左上角到右下角的主对角线及其平行线（斜率为-1的线）上，有i-j=k-l；如果这两个皇后在斜率为＋1的每一斜线上，有i+j=k+l；以上两个方程分别等价于i-k=j-l和i-k=l-j因此任两皇后的在同一斜线上的充要条件是|i-k|=|j-l|。
满足两个皇后不在同一斜线上的条件表示为：|i-k|≠|j-l|
两皇后不在同一行用式表示为：i≠k
两皇后不在同一列用式表示为：j≠l
在本文中，我们主要针对n=8的八皇后问题进行研究。

2. 遗传算法

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的一种计算模型，是一种通过模拟自然进化过程搜索最优解的方法。其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成遗传算法的核心内容。

3.编码方案

遗传算法的常用编码方案有排列编码、二进制编码、实值编码等，考虑到编码方案需要较好地对应一种棋盘皇后排列顺序，同时八皇后问题需要解决的是实体目标（即皇后）的排列问题，不涉及到浮点数层面的逼近问题，本程序采用排列编码作为编码方案，具体描述如下：
用一维n元数组x0,1…,n-1来表示一个个体，其中x[i]∈{0,1…,n-1}，x[i]表示皇后i放在棋盘的第i行第x[i]列，即第i行第x[i]列放置一个皇后。例如，x[0]=0表示棋盘的第0行第0列放一个皇后。数组第i个元素表示第i行的放置情况，可以看作一个基因。这种编码可以自然的解决了某一行只能放一个皇后的约束，如果数组的每一个元素x[i]都不重复，可以看成0 — 7的一种排列，就自然保证每一列只能放一个皇后。在编码方案实现过程中，我们对染色体编码是否可重复问题进行了讨论，经实验发现不允许染色体编码重复的方案，即每一个编码必须为0-7排列的编码方案的搜索空间为8！种，而允许编码出现重复的方案搜索空间为8^8种，在实验运行过程中第一种编码方案运行所需代数平均值比第二种方案要小一个数量级，因此最终决定采用了不允许染色体编码重复的方案，n元数组x[0,1…,n-1]中，每一个x[i]不允许重复，在程序运行过程中，无论是初始种群生成，选择，交叉，变异阶段都会维护这一编码准则。

4.初始种群

初始化种群的主要工作为：确定种群的大小及产生初始种群.种群的大小能够对遗传算法的收敛性产生很大的影响，种群较小算法收敛速度较快，但它的搜索面不够广，容易导致局部收敛；而种群较大算法收敛全局最优的概率也大，但是算法的收敛速度较慢。根据N皇后问题的特点，默认初始种群大小一般为N ~ 2N (N为皇后数)。经多次实验，初始种群大小的设置从8、12、16、24没有较大区别，对遗传代数没有突出影响，因此将默认初始种群大小设为12，界面中提供了用户自行设定初始种群大小的方法。除此之外，程序提供了两种初始种群的生成方法，第一种是随机生成，程序将自动生成用户设定数量的随机个体作为初始种群，第二种是用户输入，程序初始种群一栏提供了用户自行输入每一个个体基因编码的接口。值得注意的是，以上无论哪种方法，生成的都是0-7不含重复的8位随机排列。系统不会接受任何编码出现重复的非法个体。

5.适应度的计算

在本文中，考虑到遗传算法中优秀个体应该具有较大的适应度值，我们小组采用八皇后棋盘中不相互攻击的皇后对数作为适应度值，基于这个设定计算适应度值，易知，适应度值的最大值为28，当一个个体的适应度值为28时，说明该个体是目标解，算法停止迭代。适应度值的计算方式如下：
设a_ij表示皇后i和皇后j之间的相互不攻击系数，即：
皇后i和j的非攻击度：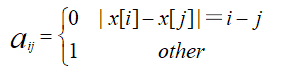
第i个皇后的非攻击度a_i表示皇后i在除自身外其余n-1个皇后中与皇后i不相冲突的数目，即有几个皇后与皇后i不攻击。如果皇后i和所有皇后都不冲突则不攻击度为n-1，与所有的皇后都冲突攻击度为0。因此，得到
同理，皇后i的攻击度表示和皇后i冲突的皇后数目，设b_i表示i的攻击度，则。
我们根据非攻击度计算：用f_i表示基因i的适应度，即第i个皇后的非攻击度，则 。如果某一个皇后i和所有其余的n-1个皇后都互不攻击，则f_i=n-1。
个体的适应度是指所有皇后的非攻击度之和，适应度函数可表示如下： 。对于一个符合解法的放置方案每一个基因的适应度都是n-1，需要指出的是，在以上推导过程没有考虑到重复计算问题，对一对由皇后i和皇后j组成的（i，j）关系，在计算皇后i和皇后j的不攻击度的时候都会计算这一对关系，为了便于理解，对上式得出的适应度
，
我们需要进行去重复计算，即

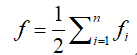
所以一个可行解的染色体的适应度是1/2 * n *（n-1） = 28（本题中，n=8）。

6.遗传算子

6.1选择算子

目前常用的选择方法有三种：比例选择、排序选择、竞技选择。
比例选择的基本思想是根据每一个个体的适应度按比例分配选择概率，适应度越大的个体选择概率越大，越容易被选择到下一代，越是优越的个体基因越容易被保留下来。比例选择实现简单，且满足遗传算法的需求，缺点在于容易产生出超级个体，另外适应度的大小有时候并不能够完全反映目标解的实际距离，易导致算法局部收敛。常用的比例选择算子有轮盘赌选择和繁殖池选择。
排序选择的基本思想是对种群中所有个体按其适应度的大小进行排序，然后根据每个个体的排列顺序，为其分配相应的选择概率，最后基于这个设定的选择概率，采用相应的比例选择方法产生下一代种群。排序选择的主要优点是消除了个体适应度差别悬殊所产生的影响，使得每个个体的选择概率仅按其在种群中的排序有关，而与其适应度的具体值无关。主要缺点是忽略了适应度值之间的实际差别，使得选择算子较少体现了个体的遗传信息，另外选择概率和序号的关系确定较麻烦。
竞技选择的基本思想是首先在种群中随机地选择k个个体进行竞标赛式比较。适应度大的个体将胜出，作为下一代种群中的个体，重复以上过程，直至下一代种群中的个体数目达到种群规模为止。参数k被称为竞赛规模，通常取k=2。这种方法实际上是将局部竞争引入到选择过程中，它既能使好的个体有较多的繁殖机会，又可避免某个个体因其适应度过高而在下一代中繁殖较多的情况。
在本程序中，我们实现了三种可选的选择算法，即轮盘赌选择，繁殖池选择，竞技选择（k=2）。实际测试中发现设计的适应度不能很好地应用于轮盘赌选择算子，原因是轮盘赌选择和繁殖池适应度按比例产生选择概率的规则即使是种群中较差的个体也具有较高的选择概率，导致算法收敛性较差，需要更多的迭代次数找到目标解，因此在参考文献之后，提出了一种针对比例选择方法提高选择概率差异的适应度改进方法，即线性标定适应度。该方法实际操作如下，对基于上节提到的适应度值（简称为传统适应度值），每一代生成的适应度值列表 （m为种群规模）找到其中最小值 ，对适应度列表中的每一个值都减去（ 产生的新的适应度列表 即为线性标定适应度。这种适应度加大了每一个基因选择概率的差异，实际测试中有效降低了所需的迭代次数。

6.2交叉算子

编码方案一定程度上决定了可操作的交叉方法，在编码方案一节中决定了本程序采用了排列编码，每一个个体由不可重复的0-7 8位排列表示，这种编码方案决定了个体从搜索空间的基因型变换到解空间的表现型时的解码方法，也影响到交叉算子的运算方法。常用的针对由排列组合问题产生的遗传算法以及基于这种基于排列的编码方案的交叉算子有Cycle Crossover (CX)，Cycle Crossover (CX)， Subtour Exchange Crossover，Order-Based Crossover (OBX)，Position-based Crossover (PBX)，Order Crossover (OX)，Partial-Mapped Crossover (PMX)等多种，这里主要介绍本程序实现的两种交叉方法OX和PMX
OX，即顺序交叉，主要原理是对于一对进行交叉的染色体parent1 和 parent2随机生成两个随机位置s，t（s < t )作为选中基因的的起始位置，生成一个子代child1 ，child1中被选中的位置（s-t）上的基因与parent1相同，然后将parent2中与第一步parent1中被选中基因不同的基因按找原来的前后顺序插入到child1中的空位中，最终产生一个符合编码方案的子代child1，用相同的方法从parent2中取出选定位置的基因并插入parent1中与被选定基因不同的基因即可产生child2，相应图示如下：
parent1：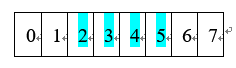
Parent2：

Child1：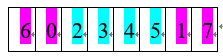
产生的另一个子代是：23560147
PMX，即部分匹配交叉，主要原理是选择一对交叉染色体中几个基因的起止位置（两染色体被选位置相同），并交换选中位置两组基因的位置，第三步做冲突检测，根据交换的两组基因建立映射关系，将生成的子代中重复基因按照映射关系处理成两个不含重复基因的子代，过程图示如下：

对产生的子代做基因映射得（1<->6<->3,2<->5,9<->4），因此处理后的子代为：

以上两种方法在交叉过程中都注保持父代中基因的相对位置，有助于遗传父代中优良的基因信息，并且维护编码方案要求。

6.3变异算子

为了保证每个个体中皇后列位置不重复，维护编码方案中行列都不重复的要求，最终方案中的变异不能使用普通遗传算法二进制编码的单点变异或者两点变异方法，通过查阅资料，我们设计了三种变异方法。
操作的基础在于编码方案要求本程序采用的编码方案要求运行中的每一个个体都必须为0-7的一个不重复8位排列。因此本文设计的变异方法对每个个体的编码排列进行变异，而不造成任何缺失和重复。
第一种，交换变异，对于给定个体编码，随机生成两位随机数k1 和 k2（0<=k1<=k2<=7)，交换个体k1和k2位置上的值，完成变异。对个体01234567，产生k1=2，k2 =5，因此变异后个体编码为01534267。
第二种，倒序变异，对于给定个体编码，随机生成两位随机数k1 和 k2（0<=k1<=k2<=7)，
将k1-k2之间共（k2+1-k1）位编码倒置顺序，完成变异。对个体01234567，产生k1=2，k2 =5，因此变异后个体编码为01543267。
第三种，插入变异，对于给定个体编码，随机生成两位随机数k1 和 k2（0<=k1<=k2<=7)，
将k1位置的编码插入到k2位置，完成变异。对个体01234567，产生k1=2，k2 =5，因此变异后个体编码为01345267。

7.终止策略

本算法采用的终止策略为：当群体中的最优个体的适应值为28时（即所有皇后都不冲突），即表示算法搜索到了一个有效解。

程序运行截图：