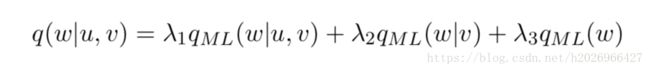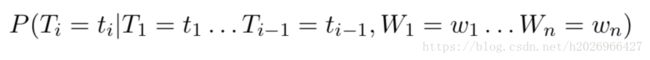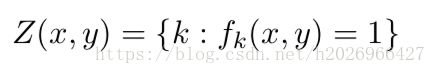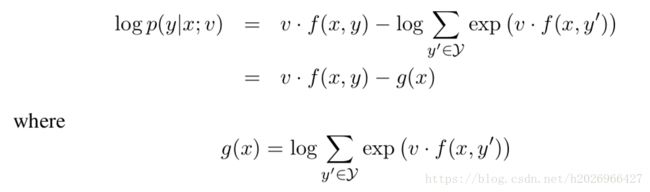Log-Linear Models
一,简介
引入
对数线性模型被广泛应用于NLP中,对数线性模型的一个关键优点在于它的灵活性:它允许非常丰富的特征集合被用于模型中。常见的对数线性模型有Logistic回归、最大熵模型、MEMMs和CRFs等。
目的
1,Trigram LM
Trigram LM还是比较有效的,但是它并没有充分使用上下文 w1,w2,...,wi−1的信息 w 1 , w 2 , . . . , w i − 1 的 信 息 。例如它在线性插值的平滑估计中只用到了三种上下文信息的特征trigram、bigram和unigram,如下式所示:
但实际上我们充分利用上下文信息的各种特征如skip bigram、词性特征、拼写特征、存在特征、搭配特征等等,如下所示:

前三个是trigram、bigram、unigram特征,剩余的分别是skip bigram、词性特征、拼写特征、存在搭配特征等。
2,POS tagging
POS tagging的目标是建模如下的条件分布:
显然在估计参数时也需要很好地合并上下文信息的各种特征。
例如下面的那些上下文特征:
总结:这种将上下文信息的各种特征通过线性插值的这种方式合并起来十分的笨重,但对数线性模型却可以非常好地将上下文的各种特征很好的合并起来!
二,对数线性模型
基本定义
特征
基本定义如下:
1,构造特征
每一个特征都会是一个指示函数,即当(x,y)符合某种条件时返回1,否则返回0。将指示函数表示成特征在NLP是及其常见的。
例如在language modeling中的特征向量的各个特征分量可以用如下指示函数来表示:
2,使用特征模板来定义特征
由于在实际中,每一个特征指示函数都是不一样的,而且它们的数量和训练语料成正比,所以,在定义它们的时候需要把那些相似的特征指示函数定义成一个特征类,即特征模版。
feature template的定义形式如下:
要注意的是所有特征模板中,特征指示函数的下标不能相同,所以需要用一个相同的哈希函数来将各种上下文信息的映射到一个不同的整数。
3,特征稀疏
由上面的定义可想而知,这个特征向量是十分稀疏的,即 fi(x,y)=1 f i ( x , y ) = 1 的数量相对于特征向量的维数d来说是十分小的!所以为了提高效率,我们需要定义一个集合:
这样在计算内积时,就可以这样计算来提高效率:
对数线性模型的形式
对数线性模型的形式如下:
内积 v⋅f(x,y) v ⋅ f ( x , y ) 是这个表达式的关键,因为它越大整个式子也越大。分母其实是一个规范化因子,保证了 ∑y∈Yp(y|x;v)=1 ∑ y ∈ Y p ( y | x ; v ) = 1 ,使输出能称为一个概率分布。
之所以叫它对数线性模型是因为:
对数线性模型的参数估计
1,最大似然估计
(1)对数似然函数如下:
(2)最大化:
但这样会出现一个问题!就是当某个特征指示函数 fk(x(m),y(m)) f k ( x ( m ) , y ( m ) ) 的值为1时,最大似然估计会促使该特征对应的权重v_k趋近于 +∞ + ∞ ,使得 p(y(m)|x(m;v)=1 p ( y ( m ) | x ( m ; v ) = 1 ,显然这会导致模型泛化能力的大大下降!
所以我们需要在对数似然函数中加入正则化來使模型有选择较小特征权重的偏好。
2,正则化的最大似然估计
(1)对数似然函数如下(此处加的是L2正则化项):
其中λ>0,可以通过验证集来选择较好的λ值。 其 中 λ > 0 , 可 以 通 过 验 证 集 来 选 择 较 好 的 λ 值 。
(2)最大化:
3,找到最优参数
由于 L(v)和L′(v) L ( v ) 和 L ′ ( v ) 都是凸函数,所以可以使用梯度下降法来求解:

其中梯度的形式如下:
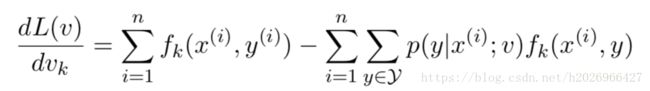
其中第一部分可以看做是训练集中 fk f k 特征出现的数量,而第二部分可以看做是训练集中 fk f k 特征出现数量的期望。
当然也可以使用改进的迭代尺度法、拟牛顿法等等,在实际中,对数线性模型的参数估计通常用的一种方法是L-BFGS,它属于拟牛顿法。