一文梳理推荐系统的中 EMBEDDING 的应用实践

“ 自Embedding的概念问世以来，Embedding的探索和应用就没有停止过，Word2Vec、Sentence2Vec、Doc2Vec、Item2Vec，甚至Everything2Vec。对，“万物皆可Embedding”。几年来，Embedding在推荐系统中的应用也越来越多，方式众多，技法新颖。”

作者：卢明冬，个人博客：https://lumingdong.cn/application-practice-of-embedding-in-recommendation-system.html

在之前的文章中，《文本内容分析算法》和《基于矩阵分解的推荐算法》文中都稍有提及Embedding的概念，由于Embedding太过重要，本文我们将详细讲解Embedding的相关知识，以及在推荐系统中的一些应用，因篇幅限制，关于Embedding在推荐系统中的应用实践我分为了两篇文章来讲述，本篇主讲Embedding以及相关延伸方法，另外一篇是大厂的Embedding实践应用，是更加偏tricks的一些应用实践总结。

Embedding的理解

Embedding，即嵌入，起先源自于NLP领域，称为「词嵌入（word embedding）」，主要是利用背景信息构建词汇的分布式表示，最终可以可以得到一种词的向量化表达，即用一个抽象的稠密向量来表征一个词。

从数学角度看，Embedding其实是一个映射（mapping），同时也是一个函数（function），即，该函数是injective（就是我们所说的单射函数，每个只有唯一的对应，反之亦然）和structure-preserving （结构保存，比如在X所属的空间上，那么映射后在所属空间上同理）的。那么对于Word Embedding，就是将单词映射到另外一个空间，这个映射也具有injective和structure-preserving的特点。

“嵌入”本身是一个数学概念。我们这里通俗理解，「如果将词看作是文本的最小单元，词嵌入本身是一种特别的映射过程，即将文本空间中的某个词，通过一定的方法，映射或者说嵌入到另一个数值向量空间，原来的整数全部变为实数，是用连续向量表示离散变量的方法。之所以称之为Embedding，是因为这种表示方法往往伴随着一种降维的意思，就像高维事物拍扁了嵌入到另一个低维空间中一样。」

Embedding这种向量化表达过程通常伴随以下变化：

• 高维——>低维

• 稀疏——>稠密

• 离散——>连续

• 整数——>实数

不难发现，「经过Embedding向量化表达后的数据，其实变得更加适合深度神经网络的训练和学习，也有利于工业界数据的工程化处理。」高维稀疏数据对于机器学习的参数学习和相关计算都不太友好（「高维易引发“维度之灾”，使空间距离很难有效衡量，另外高维经常使参数数量变得非常多，计算复杂度增加，也容易导致过拟合；稀疏容易造成梯度消失，导致无法有效完成参数学习」），因此通常特别稀疏的高维离散数据更适合使用Embedding代替传统One-Hot编码方式。

此外，「Embedding虽然是一种降维表示，但是却携带了语义信息，而且这种表示方式并不局限于词，可以是句子、文档、物品、人等等，Embedding能够很好地挖掘嵌入实体间的内部关联，即便降维也能保留这种潜在关系」，这简直就是“神来之笔”，怪不得说万物皆可Embedding。

词嵌入的维度表示某个隐含语义，一个词可能隐藏很多语义信息，比如北京，可能包含“首都、中国、北方、直辖市、大城市”等等，这些语义在所有文本上是有限的，比如 128 个，于是每个词就用一个 128 维的向量表达，向量中各个维度上的值大小代表了词包含各个语义的多少。

本质上来说，经过「Word Embedding」之后，各个单词就组合成了一个相对低维空间上的一组向量，这些向量之间的远近关系则由他们之间的语义关系决定。

因为上面提到的特性，使用Embedding可带来诸多好处：

• 不丢失信息的情况下降低维度

• 矩阵及向量运行便于并行

• 向量空间具有物理意义，比如可以根据距离比较相似性

• 可以在多个不同的维度上具有相似性

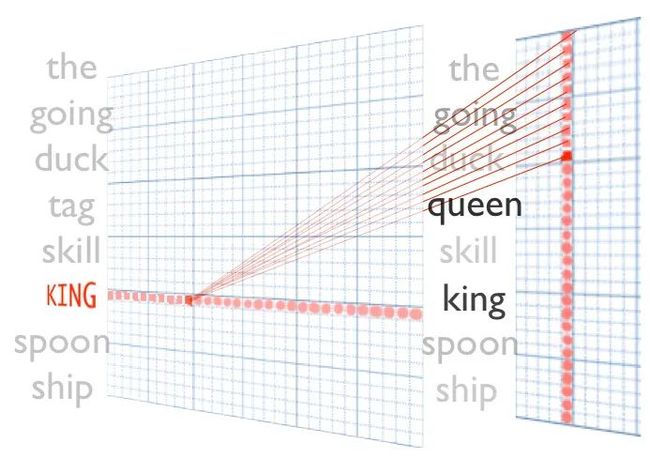
• 线性规则：king - man = queen - woman

Embedding的这种携带语义信息以及保留嵌入实体间的潜在关系的特性，使Embedding有了更多用武之地，例如：

• 「计算相似度」，比如「man」和「woman」的相似度比「man」和「apple」的相似度高

• 「在一组单词中找出与众不同的一个」，例如在如下词汇列表中：「[dog, cat, chicken, boy]」，利用词向量可以识别出「boy」和其他三个词不是一类。

• 「直接进行词的运算」，例如经典的：「woman + king-man = queen」

• 「表征文本」，如累加得到一个文本的稠密向量，或平均表征一个更大的主体；

• 「方便聚类」，会得到比使用词向量聚类更好的语义聚类效果。

• 「由于携带了语义信息，还可以计算一段文字出现的可能性」，也就是说，这段文字是否「通顺」。

上面的嵌入实体是单词，如果换成推荐物品（item），上面的一些用法，是不是让你眼前一亮呢？

Word2Vec

:books: Distributed Representations of Words and Phrases and their Compositionality

:books: word2vec Parameter Learning Explained

:books: word2vec Explained: deriving Mikolov et al.'s negative-sampling word-embedding method

词嵌入表示通常会用到谷歌提出的 Word2Vec工具库，另外fastText和TensorFlow中也可以实现Embedding的功能。这个小节我们借助Word2Vec工具的模型实现来更加深入理解Embedding。

Word2Vec的原理

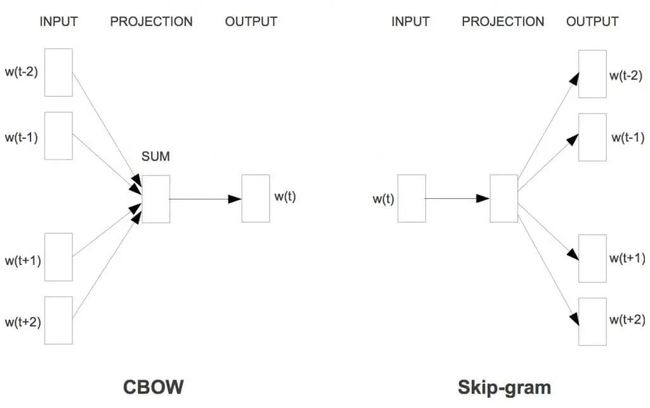
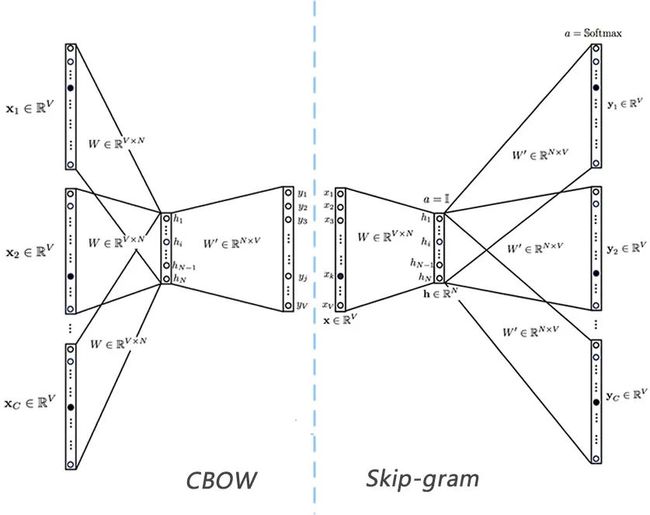
Word2Vec 是用浅层神经网络学习得到每个词的向量表达，而且在工程上进行了优化，使得百万词的规模在单机上可以几分钟轻松跑出来。它有两种网络结构，分别是CBOW（Continues Bag of Words）和Skip-gram，两种网络结构图见下图。

这两种结构都是假定每个词都跟其相邻的词的关系最密切，不同的是CBOW模型的动机是每个词都是由相邻的词决定的，所以CBOW的输入是  周边的词，预测的输出是  ，而Skip-gram模型的动机则是每个词都决定了相邻的词，输入是  ，输出是  周边的词。这里相邻的词通常由一个滑动窗口来获得，滑动窗口的长度为2c+1（目标词前后各选c个词），从句子左边滑倒右边，每滑一次，窗口中的词就形成了我们的一个正样本。如上图，这里的c设为2，其中是当前所关注的词，、、、是上下文中出现的词。

经验上讲Skip-gram的效果要更好一点，我们以Skip-gram为例，理解一下原理。上面讲到通过滑动窗口可以获取到训练样本，有了训练样本之后我们就可以着手定义优化目标了，既然每个词  都决定了相邻词，基于极大似然，我们希望所有样本的条件概率之积最大，于是有：

转为最大化对数似然：

其中，T是文本长度，即单词总数，c是窗口大小，另外单词一般需要先用One-Hot编码。

其实从上面的图中可以看出，在实际训练学习过程中，训练样本是由中心词和其上下文词组成一个个Pair对，那我们可以将目标函数写成一个更容易理解的的式子：

其中，表示中心词与其上下文词构成的样本对，是语料中所有单词及其上下文词构成的样本对集合，这里的 为「待定参数集」。

接下来的问题是怎么定义   ，作为一个多分类问题，最简单最直接的方法当然是直接用Softmax函数，同时我们希望用隐向量来表示每个词。

于是设为中心词w的词向量，为上下文词c向量，向量维度等于设置的隐藏层单元数量。整个语料共有V个单词，也就是词汇表单词数。

因此：

带入上面的目标函数，可以得到：

其中，参数是和，，是向量维度。

这两个单词的隐向量的点积表示语义的接近程度，其实点积的物理意义就是词之间的距离，点积越大，表明两个单词的语义越接近，向量点积展开如下：

（注：向量点积在不同的论文有不同的表示形式，本文为了推导后面的负例采样优化，写法与第三篇论文的写法保持一致。）

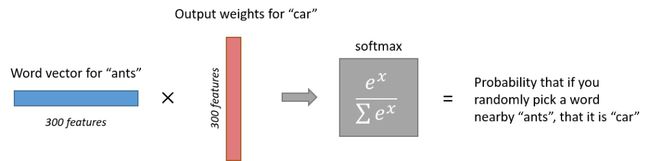
而Softmax的作用就是将点积转换成概率，下图的例子可以辅助理解[^1]：

Word2Vec的网络结构

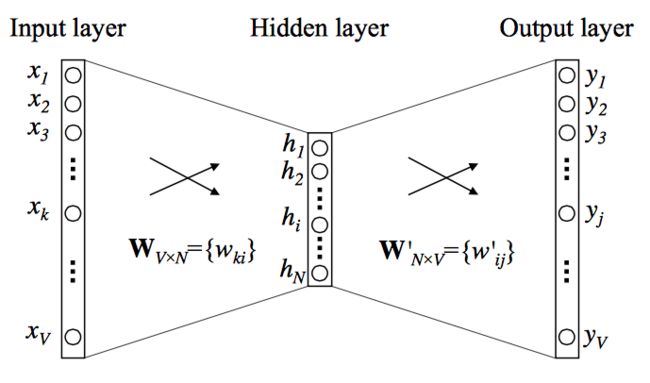
CBOW和Skip-gram都可以表示成由输入层（Input）、映射层（Projection）和输出层（Output）组成的神经网络。

输入层中的每个词通常由独热编码（One-Hot）方式表示，即所有词均表示成一个维向量，其中为词汇表中单词的总数。在向量中，每个词都将与之对应的维度置为1，其余维度的值均设为0。

在映射层（也就是隐含层）中，个隐含单元（Hidden Units）的取值可以由维输入向量以及连接输入和隐含单元之间的维权重矩阵计算得到。在CBOW中，还需要将各个输入词所计算出的隐含单元求和。需注意的是，「Word2Vec网络中的隐含层没有使用任何非线性激活函数，或者可以勉强说用的是线性激活函数（Linear Activation Function）。因为Word2Vec不是为了做语言模型，它不需要预测的更准，加入非线性激活函数没有什么实际意义，反而会降低Word2Vec的性能。」

同理，输出层向量的值可以通过隐含层向量，以及连接隐含层和输出层之间的  维权重矩阵计算得到。输出层也是一个维向量，每维与词汇表中的一个单词相对应。最后，对输出层向量应用Softmax激活函数，可以计算出每个单词的生成概率。

再之后，利用反向传播来训练神经网络的权重即可。

不过上图的网络结构是单个上下文的一个示例，即当前词预测下一个词，对于真正的多词上下文的CBOW和Skip-gram，通常是下面的结构：

以Skip-gram模型为例，其前向公式为：

因为输出层共享权重，所以都是一样的，输出向量 也是都一样的，即 。

如果想更详细地了解CBOW和Skip-gram的原理、后向传播、示例讲解等，推荐查看《The backpropagation algorithm for Word2Vec》 这篇文章。

「CBOW和Skip-gram的性能对比」

两种模型都有各自的优缺点，不过根据Mikolov的原论文，Skip-gram在处理少量数据时效果很好，可以很好地表示低频单词。而CBOW的学习速度更快，对高频单词有更好的表示。实际应用中，Skip-gram方式会更常见。

从权重矩阵到词向量

那么，到底什么才是我们想得到的Embedding向量化表示呢？

其实就是上面的「权重矩阵」和(对Skip-gram来说，分别对应损失函数公式中的中心词词向量和上下文词向量)，这「两个都可以作为最终的向量化表示矩阵」，只是一个靠近输入空间，一个靠近输出空间，具体选择哪个，理论上没有什么区别。不过我个人更倾向于选择靠近中心词一端的权重矩阵，比如CBOW选择，而Skip-gram选择，在Word2Vec使用的Skip-gram就是选的，「另外有些时候还可以尝试用两个矩阵的平均或者两个矩阵对应词向量的拼接作为最终Embedding」。

参考下图，训练完成的权重矩阵，一个维度是单词对应的维度，一个维度是隐含单元的维度，换个角度来看，它刚好就是每个词对应一个隐含特征向量，这不就是我们需要的词向量吗？因此由权重矩阵便可自然转化成Word2Vec的词向量查找表（Lookup Table）。

Word2Vec的优化方法

Word2Vec的最原本的算法在工程实现上会带来很多问题，以Skip-gram为例：

• Softmax函数中存在归一化项，因此需要对词汇表中的所有单词进行遍历，这会使得每次迭代过程非常缓慢；

• 一般情况下词汇表维度远大于词向量维度，也就是无论是输入层与隐藏层之间的权重还是隐藏层与输出层的权重，他们权重的数量都是由来决定的，而通常词表维度又是一个很大的值，也就是说，这个看似很简单的网络结构中却有大量的权重需要更新。举个例子，假设有10000个单词的词汇表，词向量维度是300，那么这两个权重矩阵的权重数量都是个，这么多的权重用梯度下降更新是非常慢的。

• 即便退一步讲，不考虑时间问题，因为权重数量越多就越容易过拟合，这时就需要大量的训练数据去调整权重以避免过拟合的发生，然而数据资源往往并没有那么容易获得。

因此，Word2Vec为了提高效率，提出了很多工程技巧对原始算法进行了优化，其中比较重要的有两个：

「层次Softmax（Hierarchical Softmax， H-Softmax）」

为了避免Softmax公式中对词汇表中所有单词遍历，「Hierarchical Softmax的思想是将原来Softmax进行拆解分层，将原Softmax的 N 分类问题转化成 logN 个二分类问题」。

这个分层转化的过程借助了「霍夫曼树（Huffman Tree）」，在网络结构中的作用是代替从隐藏层到输出Softmax层的映射，优化后，隐藏层到输出层的Softmax映射不是一下子完成的，而是沿着霍夫曼树一步步完成的，因此这种Softmax取名为"Hierarchical Softmax"。

我们先来回顾一下霍夫曼树的知识点。

霍夫曼树是带权路径长度最短的树，权值较大的结点离根较近，通常会作为一种高效的编码方式。

霍夫曼树的建立：

输入：权值为的n个节点

输出：对应的霍夫曼树

1）将看做是有n棵树的森林，每个树仅有一个节点。

2）在森林中选择根节点权值最小的两棵树进行合并，得到一个新的树，这两颗树分布作为新树的左右子树。新树的根节点权重为左右子树的根节点权重之和。

3） 将之前的根节点权值最小的两棵树从森林删除，并把新树加入森林。

4）重复步骤2）和3）直到森林里只有一棵树为止。

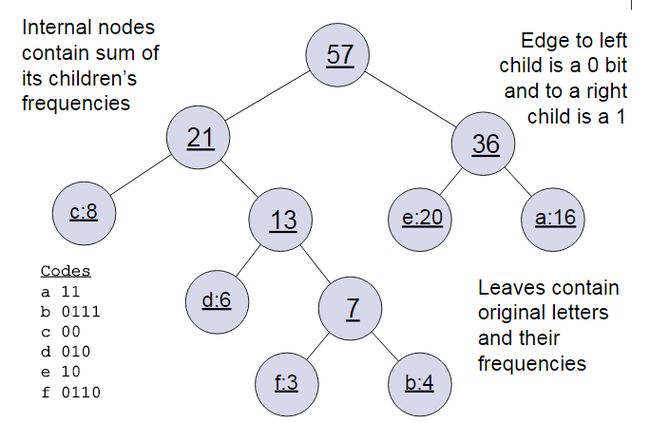
下面我们用一个具体的例子来说明霍夫曼树建立的过程：

我们有（a、b、c、d、e、f）共6个节点，节点的权值分布是（20、4、8、6、16、3）。首先是最小的b和f合并，得到的新树根节点权重是7，此时森林里5棵树，根节点权重分别是20、8、6、16、7。此时根节点权重最小的6、7合并，得到新子树，依次类推，最终得到下面的霍夫曼树。

那么霍夫曼树有什么好处呢？一般得到霍夫曼树后我们会对叶子节点进行霍夫曼编码，**霍夫曼树的构建方式决定了权重高的叶子节点越靠近根节点，而权重低的叶子节点会远离根节点，这样我们的高权重节点编码值较短，而低权重值编码值较长。这保证的树的带权路径最短，也符合我们的信息论，即我们希望越常用的词拥有更短的编码。**如何编码呢？一般对于一个霍夫曼树的节点（根节点除外），可以约定左子树编码为0，右子树编码为1。如上图，则可以得到c的编码是00。

而在word2vec中，约定编码方式和上面的例子相反，即约定左子树编码为1，右子树编码为0，同时约定左子树的权重不小于右子树的权重。

那霍夫曼树如何完成从隐藏层到输出Softmax层映射呢？

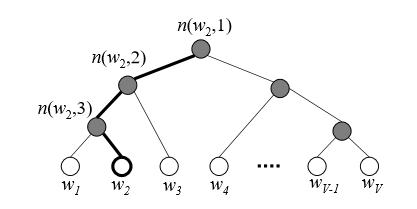
由于我们把之前所有都要计算的从输出Softmax层的概率计算变成了一颗二叉霍夫曼树，那么我们的Softmax概率计算只需要沿着树形结构进行就可以了。如下图所示，我们可以沿着霍夫曼树从根节点一直走到我们的叶子节点的词。

「这里使用霍夫曼树来代替隐藏层和输出层的神经元，霍夫曼树的叶子节点起到输出层神经元的作用，叶子节点的个数即为词汇表的小大， 而内部节点则起到隐藏层神经元的作用。」

• 叶子节点：树的每一个叶子节点都代表一个单词，所以通常词频越高离根节点越近；

• 内部节点：每一个内部节点都代表一次逻辑回归的过程，可以规定沿着左子树走是负类（霍夫曼编码1），沿着右子树走是正类（霍夫曼编码0）。假设是当前内部节点的词向量，而  则是需要学习的模型参数。对于 CBOW 模型， 初始化（根节点）为输入的词向量加和求平均后的向量，对于 Skip-gram 来说，就是  的词向量。判别正类和负类的方法是使用Sigmoid函数：

最终输出哪个单词是由 logN 次逻辑回归过程决定的，回到基于Hierarchical Softmax的word2vec本身，我们的目标就是找到合适的所有节点的词向量和所有内部节点, 使训练样本达到最大似然。如此经过一系列推导便可得到目标函数：

其中，从根节点到所在的叶子节点，包含的节点总数为, 在霍夫曼树中从根节点开始，经过的第个节点表示为，对应的霍夫曼编码为，其中。而该节点对应的模型参数表示为, 其中，没有是因为模型参数仅仅针对于霍夫曼树的内部节点。

之后利用梯度下降来更新参数：每个单词  的词向量和霍夫曼树每个内部结点的。

使用霍夫曼树有什么好处呢？首先，由于是二叉树，之前计算量为，现在变成了。第二，由于使用霍夫曼树是高频的词靠近树根，这样高频词需要更少的时间会被找到，这符合我们的贪心优化思想。可能存在的缺点是，如果训练样本里的中心词是一个很生僻的词，那么就得在霍夫曼树中辛苦的向下走很久了。[^2]

「负例采样（Negative Sampling，简称NEG，也称负采样）」

负例采样不再使用复杂的霍夫曼树，而是利用相对简单的随机负采样来大幅提高性能，并且在经过论证后发现，负例采样不但可以提高训练速度，还可以改善所得词向量的质量，因此，负例采样比层次Softmax使用率更高。

「负例采样的思想其实和层次Softmax很类似，也是将Softmax多分类问题转化成多次二分类问题，使用二元逻辑回归可以让一个训练样本每次仅仅更新一小部分的权重，不同于原本每个训练样本更新所有的权重，这样大大减少了梯度下降过程中的计算量。」

举例来讲，当我们用训练样本 (input word: "fox"，output word: "quick") 来训练我们的神经网络时，fox和quick都是经过One-Hot编码的。如果我们的单词表（vocabulary）大小为10000，在输出层，我们期望对应quick单词的那个神经元结点输出1，其余9999个都应该输出0。在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们称为“negative” word。当使用负例采样时，我们将随机选择一小部分的negative words（比如选5个negative words）来更新对应的权重。我们也会对我们的“positive” word进行权重更新（在我们上面的例子中，这个单词指的是quick）。

对于Skip-gram的输入层与隐藏层之间10000 x 300的权重矩阵，使用负例采样仅需要更新positive word即quick的和其他5个negative words的结点对应的权重，共计6个神经元，相当于每次只更新个权重，对于3百万的权重来说，相当于只计算了0.06%的权重，这样计算效率就大幅度提高。

当然，负例采样的具体过程和层次Softmax有很大区别。它的技术点会涉及两个关键的地方，一个是如何进行负例采样，另外一个是如何进行二元逻辑回归。

先来看采样方法，其实「采样方法并不是固定的」，后来很多论文中虽然使用负例采样的优化方法类进行Embedding，但是采样方法都是根据自己的业务来进行调整的，下面以原始论文中的采样方法作为参考。

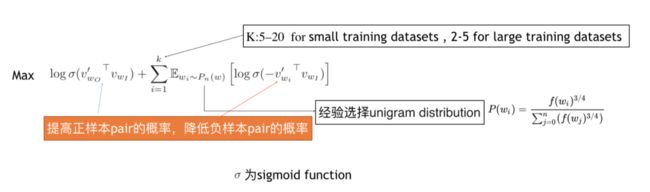
Word2Vec论文中给出的采样方式其实并不复杂，**首先采样的数量根据数据集的大小而定，一个经验是对于小数据集，选择5~20个负例，而对于较大的数据集，则只需要2~5个负例就可以。另外，采样会遵循一定的分布，这里用的是一元模型分布(unigram distribution)，它的特点是词频更高的词更有可能被选为负例，是一个加权采样。**假设我们要将整个语料库的单词作为单词表，并且从单词表中进行随机负例采样，则选取某个词的概率等于该词出现在语料库次数（词频）除以语料库出现的单词总数，用公式表示为：

其中，可以理解为计数，即得到词频。

论文中指出，作者在这个公式上尝试了很多变化，最后「表现比较好的是将单词词频提高到3/4次幂」。如下：

这个「改变后的公式会产生一个效果，就是稍微增加低频词的采样概率，降低高频词的采样概率」。可根据下图（google的搜索栏中输入“plot y = x^(3/4) and y = x”可以快速画图）的对比看出来：

「对高频词汇进行降采样避免对于这些低信息词汇的无谓计算，同时避免高频词汇对模型造成过大的影响」，注意这是一个很重要的思想，很多时候对于推荐算法中样本，都是过滤掉高频用户，保证每个用户出现的样本数近似，防止高频用户的样本对模型的过大影响，这和 CF 里面的高频用户惩罚系数一样。

然后再来看二元逻辑回归的目标函数，论文中给出了Skip-gram模型负采样的优化目标函数为：

其中就是采样用的概率分布。

原论文中并没有给出负例采样的推导过程，2014年，Yoav Goldberg在论文《word2vec Explained: Deriving Mikolov et al.’s Negative-Sampling Word-Embedding Method》里对上述目标函数给出了推导。

从本文前面的内容我们已知Skip-gram的最初的目标函数：

如果对上述目标函数进行优化，第二项需要对词典里的所有词进行优化，所以计算量比较大。如果换个角度考虑，如果我们将合理的上下文样本对看成是1，不合理的上下文样本对看成是0，那么问题转换为二分类问题，那么我们目标就是最大化下面的目标函数：

使用Softmax来定义 ：

带入目标函数：

不过这个目标函数存在问题，如果 且 足够大的话（论文中提到就能让概率接近1），就能取到最大值，这时所有的词向量都是一样的，因此最终得到的Embedding向量也就没了意义。我们需要一种机制，通过不允许某些，样本对的出现来防止所有向量具有相同的值。所以才考虑负例采样，加入负样本：

其中，是所有随机采样的负样本对，我们令，上式则可继续简化为：

这个式子基本与Mikolov提出的一样。和Hierarchical Softmax类似，接下来采用随机梯度上升法，逐步完成参数更新。

Word2Vec在推荐中的应用

Word2Vec本身就是处理文本内容的一把“利器”，因此它可以直接应用在基于内容的推荐算法中。内容推荐的一个常用方法是通过理解内容（挖掘内容属性）去挖掘用户的兴趣点来构建推荐模型，此时Embedding可以作为一个非常有效的方法来辅助理解内容，当然，这时的Embedding是依然是属于自然语言领域，也是它最本源的应用。

基于内容的推荐算法，从大多数业务的效果来看，这样的模型是有效的，也就是说用户行为与内容是相关的。不过有一点常被忽略的是：相关性是对称的！这意味着如果可以从内容属性去理解用户行为，预测用户行为，那么也可以通过理解用户行为去理解内容，预测内容属性。

Item2Vec

:books: Item2Vec: Neural Item Embedding for Collaborative Filtering

Embedding是一种很好的思想或方法，不仅仅局限于自然语言处理领域，因为嵌入式表示有众多优势，因此很快有人就尝试把这种嵌入式表示的思想应用到推荐系统中。最常见的就是构建实体的嵌入式表示，使得多种实体的嵌入式表示存在于同一个隐含空间内， 进而可以计算两个实体之间的相似性。

与Word2Vec对应，这种方法被称为Item2Vec，代表论文是微软研究人员在2016年发表《Item2Vec: Neural Item Embedding for Collaborative Filtering》。论文把Word2vec的**Skip-gram with Negative Sampling (SGNS)**的算法思路迁移到基于物品的协同过滤(Item-Based CF)上，以物品的共现性作为自然语言中的上下文关系，构建神经网络学习出物品在隐空间的向量表示。

从 Word2Vec 到 Item2Vec

首先，我们知道Word2Vec在构建样本时，需要一个个句子构成的序列。那么在推荐场景的数据集中，如何构建这个序列，或者说如何生成训练样本？

在Item2Vec中，样本数据可以有两种看待方式：

1. 基于时序

   认为item之间存在强时序关系，即前面item对后面item的产生有很大的影响，那么可以把一段时间内连续发生的item序列看作是句子，序列中的item看作是句子中的词，这样与Word2Vec的训练数据的构造就没什么区别了，因此可以直接按照Word2Vec的方法进行Embedding训练。

   基于时序的示例比如视频网站的用户观看的视频序列，音乐网站用户听的歌曲序列。

2. 基于集合

   认为item之间存在非常弱的时序关系，或者因为某种原因，我们无法获得item的序列。那么这种情况只能放弃考虑item间的时空信息，转而使用item集合来取代序列。通常我们把用户的行为序列视为一个集合（当然还有其他集合构造方式），我们假定一个静态的环境，在这个环境中，共现在同一个集合的item就可以认为它们是相似的，然后视为正样本，不管它们是以什么样的顺序产生的，如果某两个item频繁共现，二者的Embedding则可能也很相似。很明显，这种利用集合共现性构建样本的方式与Word2Vec的输入样本还是不一样的，因此无法直接应用Word2Vec的算法，这就需要对Word2Vec的过程进行调整。另外还需要注意的是，上面的这种的假设是有局限性的，不一定适用于其它场景。

   基于集合的示例比如电商网站订单中的商品集合。

到这里，再回想一下Embedding的本质是什么？是不是觉得有了更深的理解，个人理解，Embedding就是通过给定大量的关联信息，就比如上面的两种样本构建方式分别是给定上下文信息以及共现集合的关联信息，  然后通过最大似然估计的方式来计算这些关系发生概率最大时的参数，再借助于参数来赋予个体一种抽象的隐含属性并且对这些属性编码赋值的过程，到最后，这些编码过的隐含属性就能表征甚至替代这些个体，而且还保留了原始个体间的关联信息，其实这些关联信息就是通过给隐含属性编码的方式来体现的。

论文中讨论的样本构建方法是第二种，作者还提出了「两种相应的调整方式」：

1. 把Word2Vec的上下文窗口(window size)由定长的修改为变长的，窗口长度就是集合长度。其实也就是对整个item结合中的item进行两两组合构成正样本，此方法需要修改网络结构。

2. 不修改网络结构，而在训练神经网络时对物品集合做shuffle操作，变相地起到忽略序列带来对影响。

论文指出两种方法的实验效果基本一致。

Item2Vec的论文使用的是第一种调整方法，即给定一个iterm集合，SGNS的目标函数可以改为：

其中，K是集合长度，因为摒弃了序列中item的时空关系，在原来的目标函数基础上，其实已经不存在时间窗口的概念了，或者说窗口长度就是集合长度，取而代之的是item集合中两两之间的条件概率。

在论文中，作者把「中心词词向量」作为第个item的最终的向量表示，同时两个item的相似度是通过「余弦相似度」进行计算的。作者还指出，「最终的词向量也可以选用上下文词向量，甚至可以是和的向量和或和的连接来表示，后两种表示方式有时候能够产生更好的向量化表示。」

论文中将Word2Vecs模型从自然语言序列迁移到物品集合，丢失了时间和空间的序列信息，导致无法对用户行为程度建模（喜欢和购买是不同程度的行为，可以建模体现用户对不同item的喜欢程度高低）。好处是可以忽略用户－物品关系，即便获得的订单不包含用户信息，也可以生成物品集合。而论文的结论证明，在一些场景下序列信息的丢失是可忍受的。

最终论文的实验表明，使用Item2Vec对协同过滤中的item计算相应的向量化表示，在item的相似度计算上比起SVD方法要更加优越，也就是说「Item2Vec方法得到的item的向量化表示能够很好地提取item间的相似度特征」。从应用上说，Embedding也非常便于用于相似item主动检索，Item2vec甚至能够应用到错误标签的检测和纠正上，所以Item2vec具有很好的使用价值，这也使得Embedding在很多深度学习推荐系统模型中几乎成了“标配”。

「Item2Vec与MF有什么区别？」

首先，二者都应用了隐向量来表征实体特征，不同的是，传统的MF通常是user-item矩阵，而Item2Vec通过滑动窗口样本生成的方式构造出的则更像是item-item矩阵；另外，二者得到隐向量的方式也不同，MF利用均方差损失，使预测得分与已有得分之间的误差尽可能地小，而Item2Vec则是利用空间信息并借助了最大似然估计的思想，使用对数损失，使上下文关系或者共现关系构造出的正样本的item pair出现的概率可能地大；此外训练Item2Vec的时候还要引入负样本，这也是与MF不同的地方。

对于二者在推荐效果上的差异，一个经验是传统MF推荐会让热门内容经常性排在前面，而Item2vec能更好的学到中频内容的相似性。Iterm2Vec加上较短的时间窗口，相似推荐会比MF好很多。[^3]

「Embedding的在推荐下局限性」

在推荐算法中使用Embedding有个前提，item数目必须很庞大，如果item很小，估计效果就很不理想。也就是说，如果推荐的候选集很小（比如是供应商，供应商一般不会很大），此方法可能会失效。[^4]

端到端和非端到端的Embedding

Embedding的训练可以分为两种方法：「端到端（End-to-End）「和」非端到端」的训练。

「端到端（嵌入层）」

端到端的方法是将Embedding层作为神经网络的一部分，在进行BP更新每一层参数的时候同时更新Embedding，这种方法的好处是让Embedding的训练成为一个有监督的方式，可以很好的与最终的目标产生联系，使得Embedding与最终目标处于同一意义空间。（端到端的方法可参考TensorFlow中的tf.nn.embedding_lookup方法。）

将Embedding层与整个深度学习网络整合后一同进行训练是理论上最优的选择，因为上层梯度可以直接反向传播到输入层，模型整体是自洽和统一的。但这样做的缺点同样显而易见的，由于Embedding层输入向量的维度甚大，Embedding层的加入会拖慢整个神经网络的收敛速度。

❝

这里可以做一个简单的计算。假设输入层维度是，Embedding输出维度是，上层再加5层32维的全连接层，最后输出层维度是，那么输入层到Embedding层的参数数量是，其余所有层的参数总数是 。那么Embedding层的权重总数占比是 。

❞

也就是说Embedding层的权重占据了整个网络权重的绝大部分。那么训练过程可想而知，**大部分的训练时间和计算开销都被Embedding层所占据。**正因为这个原因，「对于那些时间要求较为苛刻的场景，Embedding最好采用非端到端，也就是预训练的方式完成。」

当然，端到端的Embedding层在深度模型中还是非常常见的，由于高维稀疏特征向量天然不适合多层复杂神经网络的训练，因此如果使用深度学习模型处理高维稀疏特征向量，几乎都会在输入层到全连接层之间加入Embedding层完成高维稀疏特征向量到低维稠密特征向量的转换。

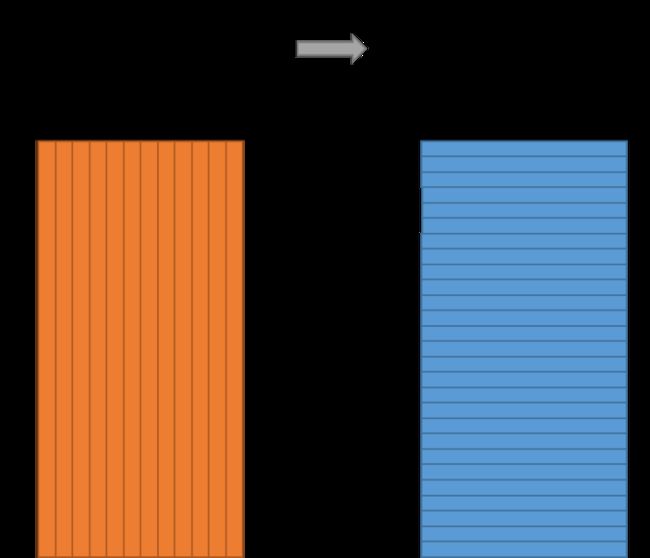
广义来说，Embedding层的结构可以比较复杂，只要达到高维向量的降维目的就可以了，但一般为了节省训练时间，深度神经网络中的Embedding层往往是一个简单的高维向量向低维向量的直接映射，如下图：

用矩阵的形式表达Embedding层，本质上是求解一个m（输入高维稀疏向量的维度）乘以 n（输出稠密向量的维度）维的权重矩阵的过程。如果「输入向量是One-Hot特征向量的话，权重矩阵中的列向量即为相应维度One-Hot特征的Embedding向量」。

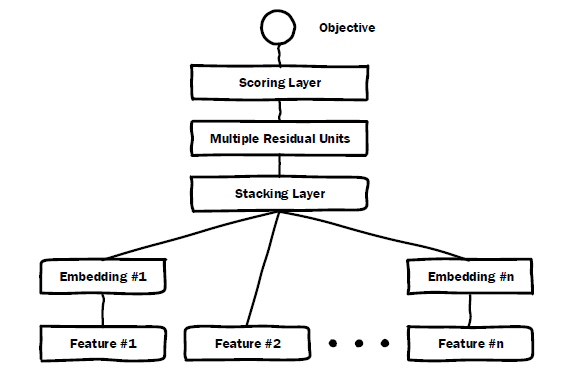
推荐系统应用实践中，使用端到端训练Embedding典型的例子，一个是微软的Deep Crossing模型：

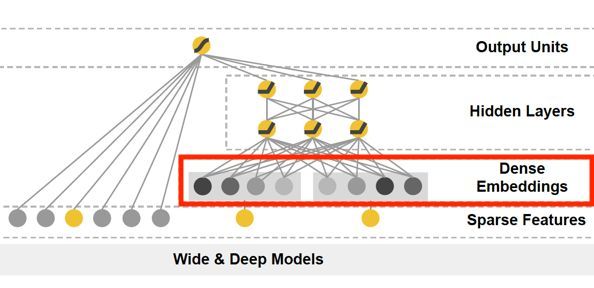
另外一个就是谷歌提出的著名的Wide&Deep模型（深度部分）：

「非端到端（预训练）」

也就是通过预训练获得Embedding，上一小节讲到的Word2Vec方法，通过语料库切分后的一堆词构建样本进行训练，其目的很纯粹，就是为了得到词向量。在真正的任务中，训练词向量并不是最终目的，而是一个预处理过程，只是为了提高最终任务模型的性能且缩短训练时间。在做其他任务时，将训练集中的词替换成事先训练好的向量表示放到网络中，就是一个非端到端的过程。在推荐场景也是一样，由于Embedding层的训练开销巨大，因此在一些时间要求比较高的场景下，Embedding的训练往往独立于深度学习网络进行，在得到稀疏特征的稠密表达之后，再与其他特征一起输入神经网络进行训练。

在自然语言中，非端到端很常见，因为学到一个好的的词向量表示，就能很好地挖掘出词之间的潜在关系，那么在其他语料训练集和自然语言任务中，也能很好地表征这些词的内在联系，预训练的方式得到的Embedding并不会对最终的任务和模型造成太大影响，但却能够「提高效率节省时间」，这也是预训练的一大好处。

但是在推荐场景下，根据不同目标构造出的序列不同，那么训练得到的Embedding挖掘出的关联信息也不同。所以，「在推荐中要想用预训练的方式，必须保证Embedding的预训练和最终任务目标处于同一意义空间」，否则就会造成预训练得到Embedding的意义和最终目标完全不一致。比如做召回阶段的深度模型的目标是衡量两个商品之间的相似性，但是CTR做的是预测用户点击商品的概率，初始化一个不相关的 Embedding 会给模型带来更大的负担，更慢地收敛。

「因此在推荐场景下，如果对于训练时间要求并不高的场景下，用端到端的训练方式可以得到更理想的效果。」

Word2Vec，Doc2Vec，Item2Vec都是典型的非端到端的方法，另外需要注意一点，「Embedding的本质是建立高维向量到低维向量的映射，而“映射”的方法并不局限于神经网络，实质上可以是任何异构模型，这也是Embedding预训练的另一大优势，就是可以采用任何传统降维方法，机器学习模型，深度学习网络完成Embedding的生成。」

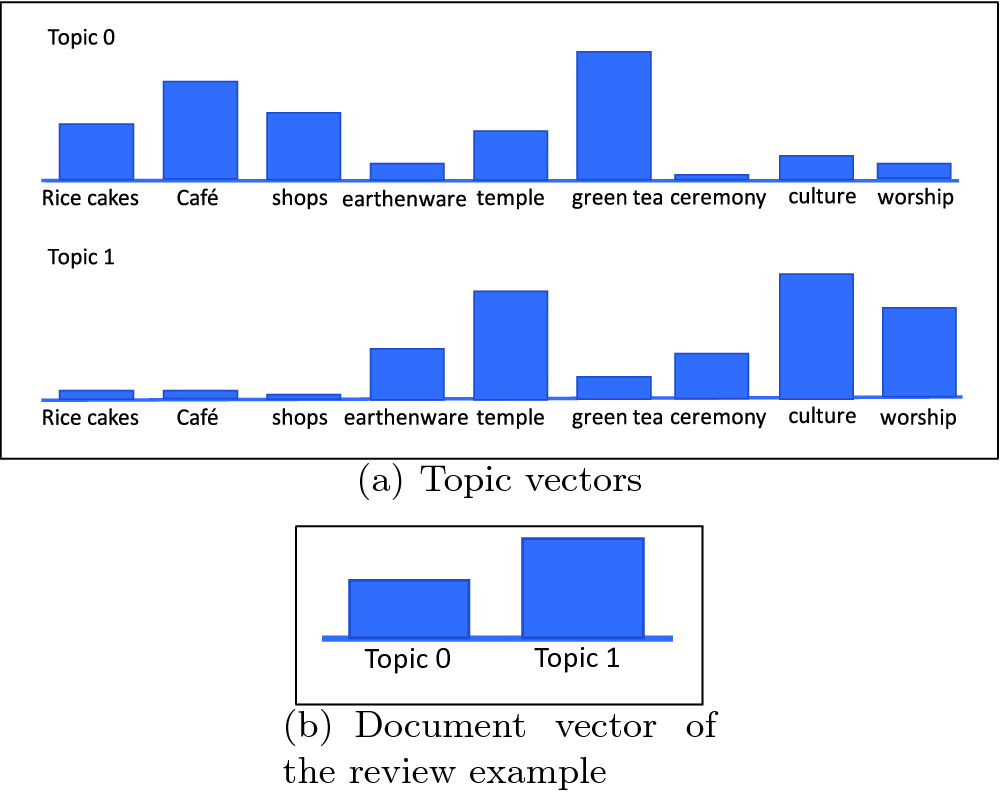
比如主题模型「LDA」可以给出每一篇文章下主题的分布向量，也可以看作是学习出了文章的Embedding：

LDA

在推荐系统应用实践中，「FNN」也可以看做是一种采用Embedding预训练方法的模型：

FNN利用了FM训练得到的物品向量，作为Embedding层的初始化权重，从而加快了整个网络的收敛速度。在实际工程中，直接采用FM的物品向量作为Embedding特征向量输入到后续深度学习网络也是可行的办法。

另外一种更加特别的例子，就是是2013年Facebook提出的著名的「GBDT+LR」的模型，其中GBDT的部分本质上也是完成了一次特征转换，可以看作是利用GBDT模型完成Embedding预训练之后，将Embedding输入单层神经网络进行CTR预估的过程。

2015年以来，随着大量Graph Embedding技术的发展，Embedding本身的表达能力进一步增强，而且能够将各类特征全部融合进Embedding之中，这使Embedding本身成为非常有价值的特征。这些特点都使Embedding预训练成为更被青睐的技术途径。

诚然，将Embedding过程与深度网络的训练过程割裂，必然会损失一定的信息，但训练过程的独立也带来了训练灵活性的提升。举例来说，由于物品或用户的Embedding天然是比较稳定的（因为用户的兴趣、物品的属性不可能在几天内发生巨大的变化），Embedding的训练频率其实不需要很高，甚至可以降低到周的级别，但上层神经网络为了尽快抓住最新的正样本信息，往往需要高频训练甚至实时训练。使用不同的训练频率更新Embedding模型和神经网络模型，是训练开销和模型效果二者之间权衡后的最优方案。[^5]

Embedding质量的评估

虽然目前Embedding的应用已经十分火热，但对其评价问题，即衡量该Embedding训练得是好是坏，并没有非常完美的方案。实际上，评价其质量最好的方式就是以Embedding对于具体任务的实际收益（上线效果）为评价标准。但是若能找到一个合适的方案，可以在上线前对得到的Embedding进行评估，那将具有很大的意义。

我们这里分Word Embedding和Item Embedding来分别讨论二者的度量方案。

Word Embedding有较多的比较成熟的度量方案，常用的有以下几种[^6]：

1. 「Relatedness」

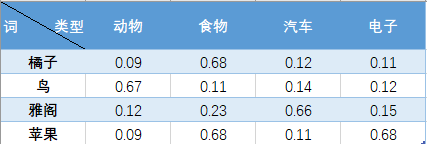
   Relatedness:task(相似度评价指标，看看空间距离近的词，跟人的直觉是否一致)目前大部分工作都是依赖wordsim353等词汇相似性数据集进行相关性度量，并以之作为评价Word Embedding质量的标准。这种评价方式对数据集的大小、领域等属性很敏感。Google在Word2Vec中给出的评估方案就是这个。示例如图：

   

2. 「Analogy」

   Analogy:task也就是著名 A - B = C - D 词汇类比任务（所谓的 analogy task，就是Embedding线性规则的体现，如 king – queen = man – woman）。

   示例如图：

   

3. 「Categorization」Categorization分类，看词在每个分类中的概率。

   示例如图：

   

4. 「聚类算法」例如 kmeans 聚类，查看聚类分布效果 。若向量维度偏高，则对向量进行降维，并可视化。如使用pca，t-sne等降维可视化方法，包括google的tensorboard以及Embedding Projector，python的matplotlib等工具，从而得到词向量分布。

   示例如图：

   

Item Embedding则基本上没有统一认可的方案，下面提供一些方案提供参考：

1. 一个常用的评估的办法就是采样看Top N的相似度，看是不是确实学习到了有意义的信息，下一节提到的阿里EGES论文中，用的就是这样的方法。

2. 从item2vec得到的词向量中随机抽出一部分进行人工判别可靠性。即人工判断各维度item与标签item的相关程度，判断是否合理，序列是否相关。

3. 也可以借鉴Word Embedding中聚类可视化的方法，抽样进行对比，查看效果如何。

4. 还有一种方案，就是用大量数据训练出一个相对新的类似于 wordsim353 标准的 item 类型的标准，之后进行相似度度量。但是实现难度主要在训练数据的质量和时效性方面，对于商品类还好，但对于新闻类这种更新率极快的 item 类型，时效性是很大问题。

5. 当然，也可通过观察实际效果来定，也可采用替换 Embedding 对应值为初始值来看预测效果是否有显著下降。

Graph Embedding

Word2Vec 通过序列（sequence）式的样本：句子，学习单词的真实含义。仿照 Word2Vec 思想而生的 Item2Vec 也通过商品的组合去生成商品的 Embedding，这里商品的组合也是序列式的，我们可以称他们为“Sequence Embedding”。然而，在更多场景下，数据对象之间更多以图（网络）的结构呈现，这种结构生成Embedding的方法，我们称之为图嵌入（Graph Embedding）。例如下图，由淘宝用户行为数据生成的物品关系图（Item Graph）：

从上图的例子中，我们已经能触碰到一些 Graph Embedding 的本质。Graph Embedding 之所以能好于 “Sequence Embedding”，是因为 Graph Embedding 能够生成一些“不存在”的序列。例如，上图数据中没有这样的用户行为数据：B-E-F、D-E-C等等。但是在物品关系图中，我们有机会生成这样的序列。

图结构比Item2Vec更能反映一些实际场景下的复杂关系网络，更能捕获Items间的高维相似性。如今 Graph Embedding 已经是推荐系统、计算广告领域非常流行的做法，并且在工业实践中也取得了非常不错的线上效果。

Graph Embedding有很多类似的称呼，图（Graph）有时会称为网络（Network），因此，有些地方还会称把Graph Embedding称为网络表示学习（Network Representation Learning）。类似的，我们还会经常看到 Network Embedding、Node Embedding、Graph Representation 等等 ，这些名词可能在定义上会有差异，大部分时间，我们可以在特定场合将他们视为同义词。

Graph Embedding的相关算法有很多，我们这里介绍几个关键的算法。

DeepWalk

:books: DeepWalk: Online Learning of Social Representations

训练Embedding的一个重要过程是构建含有关系的样本（我这里姑且称这种样本为关系样本），然后作为Skip-gram模型的输入，虽然从“一维”序列（sequence）变成了“二维”的图（graph），但训练Embedding的核心算法基本是没有变的，「关于Graph Embedding的相关研究，很大一部分其实是研究如何更好地构建这种关系样本，其中包括如何更合理地构造图，如何更合理地从图中采样得到关系样本，从而能够在Embedding中更好地保留这些关系」。DeepWalk其实就是这样，它并没有在训练Embedding的模型上动手，因此只有输入更合理的关系样本数据，才能得到更好的Embedding向量化结果，这也是图结构存在的意义之一。既然模型没有变，那么模型要求的输入也和原来一样，我们自然也需要提供和序列采样出的类似的关系样本数据，只不过现在高了一个维度，于是整个样本构建的流程就变成了先按照业务关系构造图，然后从图采样到序列，再从序列采样到样本，才能作为Embedding训练模型的输入，如下图：

其中各个环节的采样和转化都关系到最终效果的好坏，这也是大家研究和优化的重点内容。

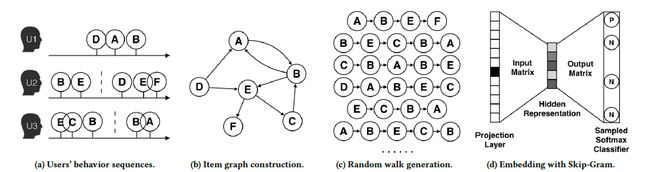
DeepWalk是2014年提出的影响力较大的Graph Embedding方法，也是最基础的Graph Embedding方法，它重点解决的就是如何从图采样到序列，其主要思想是在由物品组成的图结构上进行「随机游走（Random Walk）」，产生大量物品序列，然后将这些物品序列作为训练样本输入word2vec进行训练，得到物品的Embedding。

上图中展示的是阿里在淘宝上的DeepWalk的过程，在传统DeepWalk的基础上，阿里的还应用了会话切分和加权边，具体过程如下[^7]：

1. 图a展示了原始的用户行为序列，「这里设置了一个时间窗口，只选择用户在该窗口内的行为」，这样处理不但可以节省计算和存储开销，也符合一个用户的兴趣趋向于随时间迁移的实情。这种处理方法被称为是基于session的用户行为（session-based）。经验上，该时间窗口的区间是一个小时；

2. 图b基于这些用户行为序列构建了物品相关图，可以看出，物品A，B之间的边产生的原因就是因为用户U1先后购买了物品A和物品B，所以产生了一条由A到B的有向边。**如果后续产生了多条相同的有向边，则有向边的权重被加强。**在将所有用户行为序列都转换成物品相关图中的边之后，全局的物品相关图就建立起来了；

3. 「图c采用随机游走的方式随机选择起始点，重新产生物品序列」；

4. 图d最终将这些物品序列输入word2vec模型，生成最终的物品Embedding向量。

随机游走是一种路径搜索算法，用来从图上获得一条随机的路径。从一个节点开始，随机沿着一条边正向或者反向寻找到它的邻居，以此类推，直到达到设置的路径长度。不难发现随机游走有两个关键步骤，第一，起始节点的选择；第二，下一跳节点的选择。

其中，起始节点的选择有两种常见做法：

1. 按照一定的规则（比如均匀抽样）随机从图中抽取一定数量的节点；

2. 以图中所有节点作为起始节点。

一般来说我们选择第2种方法，以使所有节点都被选取到。[^8]

下一跳节点的选择，有很多方案，包括后面介绍的几种Graph Embedding算法，很多也是在下一跳的选择上进行优化研究，我们这里先列举几个简单的基础方法：

1. 对于无权图，无差别的从当前节点的邻居中随机采样节点作为下一个访问节点，重复此过程，直到访问序列长度满足预设条件。DeepWalk论文中的就是用的这种纯粹的随机游走方法；

2. 对于有权图，下一跳节点的选择最简单的方法是按照边的权重随机选择，阿里的论文在讲述DeepWalk的时候，给出了一个非常简单的「随机游走转移概率」的公式，也就是到达节点后，下一步遍历的临接点的概率。

   如果物品的相关图是有向有权图，那么从节点跳转到节点的概率定义如下：

   其中是节点所有的出边集合，是节点到节点边的权重，表示节点 到 没有边的情况。

   如果物品相关图是无向无权重图，那么跳转概率将是上面公式的一个特例，即权重将为常数1，且应是节点所有“边”的集合，而不是所有“出边”的集合。

使用随机游走带来的好处：

• 「并行化」，随机游走是局部的，图的规模比较大的时候，可以同时在不同的顶点开始进行一定长度的随机游走，多个随机游走同时进行，可以减少采样的时间。

• 「适应性」，可以适应图的局部的变化。图的的演化通常是局部的点和边的变化，这样的变化只会对部分随机游走路径产生影响，因此在图演化的过程中不需要每一次都重新计算整个图的随机游走。

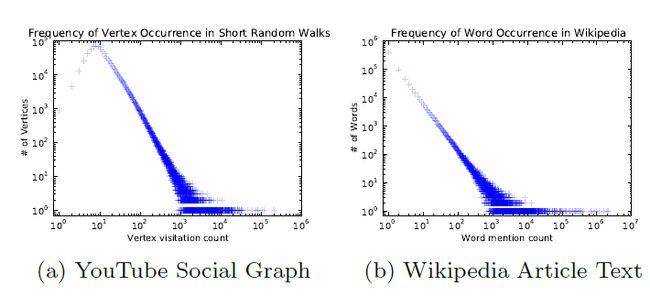
• 「解释性」，论文中提到，在图中通过随机游走得到序列的节点分布规律与NLP中句子序列在语料库中出现的词频规律有着类似的幂律分布特征，见下图。在自然语言里面，幂律分布特征可以理解为只有少量的单词出现频率非常高，而绝大部分的单词出现的频率较低，还可以理解为，在日常交流中，常用的词汇很少，而绝大部分的词汇并不常用，可以看出随机游走路径显然符合自然语言的特点，从某个角度说明随机游走采样生成序列的合理性。

  

DeepWalk的算法流程：

参数更新过程：

LINE

:books: LINE: Large-scale Information Network Embedding

DeepWalk 之后，比较重要的工作是微软亚洲研究院在 2015 年发布的 LINE（Large-scale Information Network Embedding）。LINE中定义了两种相似度来进一步深化“节点关系”，使训练出的Embedding既保留局部网络结构信息又保留了一定的全局网络结构信息。

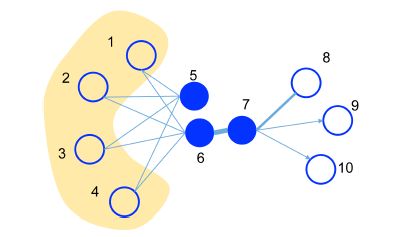
First-order proximity（一阶相似度）：用于描述图中成对顶点之间的局部相似度，形式化描述为若节点之间存在直连边，则边的权重即为两个顶点的相似度（权重可以是0-1这样的二进制表示，也可以是任意的非负数），若不存在直连边，则一阶相似度为0。如下图，节点 6 和 7 之间存在直连边，且边权较大，则认为两者相似且一阶相似度较高，而 5 和 6 之间不存在直连边，则两者间一阶相似度为 0。

Second-order proximity（二阶相似度）：网络中的很多相互关系其实不一定能够直接观察到，仅有一阶相似度并不能保留全局网络结构，因此作为补充，加入了二阶相似度。二阶相似度并不是通过直接观察到的连接来确定的，而是通过顶点的共享邻域结构来确定的。如下图，虽然节点 5 和 6 之间不存在直连边，但是他们有很多相同的相邻节点 （1,2,3,4），这其实也可以表明5和6是相似的，二阶相似度就是用来描述这种关系的，拥有相似邻居的顶点往往彼此相似。其实二阶相似度也是符合自然的直觉的，例如，在社交网络中，拥有相同朋友的人往往有相似的兴趣，从而成为朋友；在单词共现网络中，总是与同一组词同时出现的词往往具有相似的含义。二阶相似度形式化定义为，令表示顶点  与所有其他顶点间的一阶相似度，则  与  的二阶相似度可以通过  和  的相似度表示。若与之间不存在相同的邻居顶点，则2阶相似度为0。

LINE

相比 DeepWalk 纯粹随机游走的序列生成方式，LINE 可以应用于有向图、无向图以及边有权重的网络，并通过将一阶、二阶的邻近关系引入目标函数，能够使最终学出的 node embedding 的分布更为均衡平滑，避免 DeepWalk 容易使 node embedding 聚集的情况发生。下图是论文中的结果对比：

从图中可以看出，LINE 的效果最好，DeepWalk 对不同颜色的点分得也不错，但是图形中部很多点都挤在一块，而这些点都是出度很大的点，文章提了一句说对于这种点的处理 DeepWalk 会产生很大噪音，但没有详细对此分析。论文还指出，**DeepWalk 利用随机游走去捕获邻近关系，更像是深度优先搜索DFS；而LINE的方式更像是广度优先搜索BFS，相对而言更合理。**上图中的 GF 代表 graph factorization，这里不作介绍。[^9]

Node2Vec

:books: node2vec: Scalable Feature Learning for Networks

在 DeepWalk 和 LINE 的基础之上，斯坦福大学在 2016 年发布了 Node2Vec。Node2Vec是一种综合考虑DFS邻域和BFS邻域的Graph Embedding方法。简单来说，Node2Vec可以看作是DeepWalk的一种扩展，是可以控制随机游走呈现DFS还是BFS的DeepWalk，进而实现不同关系序列的均衡。

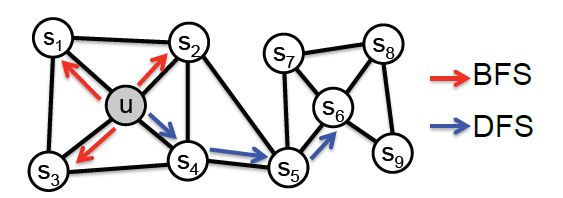
Node2Vec把领域的采样看作是局部搜索的一种形式，通常分为两种极端采样策略：广度优先采样（Breadth-first Sampling，BFS）和深度优先采样（Depth-first Sampling，DFS），下图能够明显看出这两种采样方式的不同。

广度优先抽样(BFS)：邻域被限制在起始节点的近邻节点上，与初始节点在同一社区内的节点更容易出现在一个路径里。在上图中，对于大小为k=3的领域采样，BFS采样节点s1、s2、s3。

深度优先抽样(DFS)：邻域由在距离起始点越来越远的连续采样的节点组成，发现能力更强。在上图中，对于大小为k=3的邻域采样，DFS采样节点s4、s5、s6。

论文指出，通常在网络中存在着两种相似性，即「同质性（homophily）「和」结构性（structural equivalence）」。

同质性通常是那些高度互联且属于类似网络集群或社区的节点，同质性表示内容相似，它们Embedding应该也尽量近似。如上图中，节点u与其相连的节点s1、s2、s3、s4的embedding表达应该是接近的，这就是“「同质性」“的体现。

结构性指的是在网络中具有类似结构作用的节点，结构性表示结构相似，它们的Embedding也应该尽量接近，需注意的是，结构相似并不强调连接性，即使节点在网络中可能相距很远，仍然可以具有相似的结构。如上图中节点u和节点s6都是各自局域网络的中心节点，结构上相似，其Embedding的表达也应该近似，这是“「结构性」”的体现。

「论文发现，BFS和DFS采样策略在产生反映上述两种对应关系的向量表示方面发挥着关键作用。DFS擅长学习网络的同质性，BFS擅长学习网络的结构性。」

这个结论特别容易理解反了，具体该怎样理解呢？[^10]

❝

知乎网友：（個人理解）如果把上面的Graph的某一个作为Root，然后画一个树状结构去搜索，BFS和DFS就好理解了。

❞

对于广度优先搜索（BFS）来说，其搜索往往是在当前节点（这里以节点u为例）的邻域进行的，特别是在node2vec中，由于存在所谓的“返回概率”，所以即使从u搜索到了s1，也有很大概率从s1再返回u，所以BFS产生的序列往往是在u附近的节点间进行来回的震荡，这就相当于对u周围的网络结构进行了一次「微观扫描（microscope view）」。

那么这个微观扫描当然更容易得到「微观结构」的观察，所以BFS就更容易使Embedding结果更多反应网络的“结构性”。这里我需要纠正一下大家对“结构性”的理解，正如上面所说的一样，这里的“结构”更多的指的是微观结构，而不是大范围内，甚至整个网络范围内的宏观结构，而是一阶、二阶范围内的微观结构。

再举个例子理解一下，比如对于节点u和节点s9这两个节点来说，节点u是局部网络的中心节点，节点s9是一个十分边缘的节点。那么在对这个网络进行多次BFS随机游走的过程中，节点u肯定会被多次遍历到，而且会与s1-s4等更多节点发生联系，而边缘节点s9无论从遍历次数，还是从邻接点的丰富程度来说都远不及节点u，因此两者的Embedding自然区别很大。

如果用DFS进行遍历，由于遍历存在更大的不确定性，因此s9有更大的可能被包含在更多的序列中，并跟更多的节点发生联系，这就减弱了局部结构性的信息。类似于平滑了结构性的信息，自然是不如BFS更能反应“微观结构”了。

另一方面，「为什么说DFS更能反应“同质性”呢」？

这里还要对“同质性”也进行一个纠正，这里的“同质性”不是指一阶、二阶这类非常局限的同质性，而是在相对较广范围内的，能够发现一个社区、一个群、一个聚集类别的“同质性”。要发现这类同质性，当然需要使用DFS进行更广范围内的探索。如果仅用BFS在微观范围内探索，如何发现一个社区的边界在哪里呢？

所以，「DFS相当于对网络结构进行了一次宏观扫描」（macroscope view），只有在宏观的视角，才能发现大的集团、社区的聚集性，和集团内部节点的“同质性”。

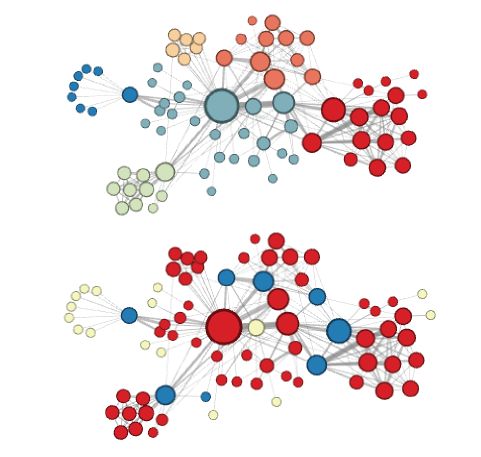
论文中最后通过实验的方式验证了DFS和BFS对于“同质性”和“结构性”的挖掘结果。颜色接近的节点代表其Embedding的相似性更强，节点也比较相似。

其中，上部分的参数 p = 1，q = 0.5，表现为更倾向于DFS的结果（详细控制公式和参数见下面内容），可以看到各聚类的内部节点相似，这是网络“同质性”的体现；而下部分参数 p = 1，q = 2，表现为更倾向于BFS的结果，结构类似节点的Embedding更为相似，这是“结构性”的体现。

同时，论文给出了一个可以控制广度优先或者深度优先的方法，进而进一步权衡控制同质性和结构性相似的Embedding关系的学习。

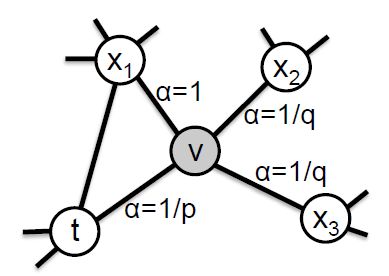
其实DFS还是BFS，主要还是通过节点间的跳转概率来控制的，以下图为例，我们假设第一步是从t随机游走到v后，这时候我们要确定下一步的邻接节点。

形式化来讲，从节点跳转到下一个节点的概率为：

其中，是边的权重，的定义如下：

其中，指的是节点到节点的距离，只有0，1，2三种取值。当时，表示就是本身，相当于下一节点选择的是，即往回走的情况；当，则表示和直接相连，比如下一节点选图中的，这种情况通常会将连接的三个结点构成一个三角形，如、、三个结点；当时，则下一节点和不直接相连，比如当为图中的或者时。

上式利用参数和共同控制着随机游走的倾向性，来选择BFS 还是 DFS，从而控制对结构性或同质性网络关系的学习。

参数被称为「返回参数（return parameter）」，控制跳回到前序节点的概率，越小，随机游走回退到节点的可能性越大，如果，则更倾向于搜索局部周边的节点，则产生的序列与宽度优先搜索（BFS）类似，更加擅长学习到网络的结构性；相反，越大，游走越不会访问到之前的节点，如果，刚刚访问过的节点不太可能被重复访问，则更倾向于搜索更大范围，产生的序列与深度优先搜索（DFS）类似，更加擅长学习到网络的同质性。

参数被称为「进出参数（in-out parameter）」，控制下一跳节点选择与不直接相连节点的概率，当  时，节点  之后更倾向于访问前序节点  的共同邻居，当前节点更可能在附近节点游走，产生的序列与宽度优先搜索（BFS）类似，更加擅长学习到网络的结构性；q < 1 时，节点  之后，更不倾向访问前序节点 t 的邻居，则随机游走到远方节点的可能性越大，产生的序列与深度优先搜索(DFS)类似，更加擅长学习到网络的同质性。

上面这种随机游走策略和当前节点，前序节点相关，其实是二阶马尔科夫。

一般来说，我们会从每个点开始游走5~10次，步长则根据点的数量N游走步。[^8]

Node2Vec的算法流程：

Node2Vec所体现的网络的同质性和结构性在推荐系统中也是可以被很直观的解释的。「同质性相同的物品很可能是同品类、同属性、或者经常被一同购买的物品」，而「结构性相同的物品则是各品类的爆款、各品类的最佳凑单商品等拥有类似趋势或者结构性属性的物品」。毫无疑问，二者在推荐系统中都是非常重要的特征表达。由于Node2Vec的这种灵活性，以及发掘不同特征的能力，甚至可以把不同Node2Vec生成的Embedding融合共同输入后续深度学习网络，以保留物品的不同特征信息。

EGES

:books: Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba

Graph Embedding能够保留一些CF忽略了的复杂的高阶相似网络关系，但是它有一个致命的弱点，就是“冷启动”问题。如果单纯使用用户行为生成的物品相关图，固然可以生成物品的Embedding，但是如果遇到新加入的物品，或者没有过多互动信息的长尾物品，推荐系统将出现严重的冷启动问题。「为了使“冷启动”的商品获得“合理”的初始Embedding，阿里团队通过引入了更多补充信息来丰富Embedding信息的来源，从而使没有历史行为记录的商品获得Embedding。」

这便是2018年阿里公布的其在淘宝应用的Embedding方法「EGES（Enhanced Graph Embedding with Side Information）」，其基本思想是在DeepWalk生成的Graph Embedding基础上引入Side Information。

「Side Information，可以简单理解为用户或物品的相关属性信息，我们通常会称之为用户侧信息、物品侧信息。」

「在推荐系统中常用的特征源有：用户对物品的历史行为交互信息、发生交互的上下文环境信息、用户侧或者物品侧的属性信息、通过属性信息连接的拓扑结构延伸出的知识图谱信息。」

接下来我们简单分析一下这种方法背后的思想是什么。

「生成 Graph Embedding 的第一步是生成物品关系图，我们通常只是通过用户行为序列来生成物品关系图。其实我们也可以通过物品侧信息（Side Information）的相似性来建立物品之间的边，比如利用相同品牌、相同类别等信息，这样就可以生成基于内容物品关系图，有了这个物品关系图，自然可以在没有用户行为的情况下也能够学习到 Embedding，也一定程度上缓解了冷启动问题。」

基于这种物品侧属性信息生成的物品 Embedding 向量可以被称为 Side Information Embedding 向量，当然，根据使用的物品侧信息类别的不同，可以有多个 Side Information Embedding 向量[^7]。比如对于淘宝的商品，这些 Side Information 可以是类目、店铺、价格、品牌等等，其实就是物品在某一个方面的属性内容信息，叫 Side Information 确实也形象，「Side Information 通常在排序阶段被广泛用作关键特征，但在召回阶段应用较少」。

「GES和EGES模型」

通过随机游走，我们可以得到 item 的游走序列，包括了之前有行为的item以及新加入的item，每个item都对应一组Side Information，也就意味着我们同时得到了Side Information序列，此时需要将item 和Side Information一起加入Skip-gram模型进行训练学习，否则不在一个向量空间，做运算无意义。

因此，对于每个 item，最后除了会得到它对应的 item Embedding，还有有各个Side Information产生的Embedding，那么如何融合一个物品的多个Embedding向量，使之形成物品最后的Embedding呢？最简单的方法是在深度神经网络中加入average pooling层将不同Embedding平均起来，用公式表示为：

其中，是item v的聚合Embedding，我们使用来表示items或者Side Information的Embedding Matrix。特别的， 表示item v的Embedding，表示绑定到item v上的第s个类型的Side Information的Embedding。因此，对于item v，使用n种类型的Side Information，我们将有n+1个向量，d是Embedding的维度。注意，「item Embeddings和Side Information Embeddings的维度，经验上设置为相同的值。」

在论文中上述方法称为GES（Graph Embedding With Side Information），「通过这种简单的方法将Side Information加了进来，从而使具有相近Side Information的item可以在Embedding空间内更接近。这会使冷启动item的Embedding表征更加精准，同时因为内容属性的加入，丰富了向量表达，进一步提升了在线和离线的效果。」

阿里团队在上述方法的基础上，将平均进一步改为加权平均的方式，也就是最终的EGES（增强型的EGS，Enhance Graph Embedding With Side Information）方法，这样的改动也更加符合实际情况，因为不同类型的Side Information对最终的Embedding的贡献是不可能相等的。例如，一个购买了IPhone的用户，趋向于会浏览Macbook或者Ipad，因为品牌都是”Apple”；而一个购买了多个不同品牌衣服的用户，出于便利和更低价格，还会在相同的淘宝店上继续购买。因此，「不同类型的Side Information对于在用户行为中的共现item的贡献各不相同」。

EGES使用了一个加权平均层（weighted average layer）来结合不同的Side Information，定义如下：

其中，设 v 是给定的一个item，是权重矩阵（weight matrix），是第个item、第个类型Side Information的权重。注意，，即A的首列，表示item v的自身权限。出于简洁性，我们使用来表示关于第v个item的第s个类型的Side Information的权重，表示item v自身的权重。另外**我们使用来替代，一是避免权重为0，二是因为在梯度下降过程中有良好的数学性质。**分母 被用于归一化不同类型Side Information的Embeddings的相关权重。

「EGES」的流程如下图：

该模型将传统Skip-gram模型进行了改进，加入Side Information以及加权平均层，成为Weighted Skip-gram模型，其中：

1. SI 表示Side Information，SI 0表示item本身，剩下的SI 1 ~ SI n 表示item对应的几种Side Information；

2. Sparse Features代表 item 和 Side Information 的ID信息，通常用One-Hot编码表示；

3. Dense Embeddings 表示 item 和 Side Information 的 Embedding 信息，并在Hidden Representation处进行加权平均聚合；

4. Sampled Softmax Classifier表示使用负例采样的优化方式，N代表采样的负样本，P代表正样本（某个item周边上下n个item均为正样本，在模型中表示时不区分远近）。

EGES的算法流程：

「Side Information带来的好处」

1. 「提升Embedding的表征力度」

   Side Information加入Embedding的训练，除了用到原本用户的行为信息，又加入了物品的内容属性信息，这样可以极大丰富 item Embedding的表征力度，因为用户的偏好跟这些物品内容属性也可能有很大的关联。

2. 「为解决item冷启动提供了便利」

   新的item是没有用户交互信息的，因此也就无法训练Embedding，没有Embedding也就无法有效推荐新物品，这是一个很棘手的问题。不过这个新item会有品牌、店铺、价格、类目等一系列内容属性信息，即Side Information，Side information都是有现成的训练好的Embedding。因此，「可以借用Side Information训练好的Embedding来解决item的冷启动问题，通常的做法是，根据item内容属性所关联的Side Information，将这些Side Information对应的Embedding计算向量平均值，作为冷启动item的Embedding向量。」

   下图是论文在获取到冷启动item的Embedding后，比较了与冷启动item的Embedding最相似的Top 4个物品，用来评估Embedding的质量。从结论来看，相似的Embedding确实有很多相似的Side Information，这种冷启动方法效果还不错。

总结

文本首先深入介绍Embedding的相关内容，然后介绍了Embedding在推荐系统中几种常见的应用方法，其中，Word2Vec可以直接作为文本解析工具来辅助完成一些基于内容的推荐，而Item2Vec则是Word2Vec在推荐系统领域的一个转化，也是最基本最常见的Embedding应用，Item2Vec借助基于物品的协同过滤，得到item的向量化表征，从而使item方便获得更深层次的关联信息。最后，我们介绍了当下流行的Graph Embedding，Graph Embedding比Item2Vec能够获得更加高阶的相似和关联信息，其中DeepWalk使用随机游走的方式从Graph中获取到序列，LINE方法则提出两种不同的相似度概念，并提出BFS和DFS的一些区别，Node2Vec则进一步提出一种控制方案，可以通过控制游走方式呈现BFS还是DFS来平衡学习“同质性”和“结构性”的相似关系，最后我们介绍了阿里的EGES，该方法引入了Side Information来缓解物品的冷启动，也通过加权平均将多种Side Information Embedding聚合成最终的Embedding，使得最后的Embedding除了保留了用户行为序列中物品的共现性，还加入了Side Information中的内容关联信息，使得item的Embedding表征更加丰富。

参考资料

[^1]: 天雨粟. 理解 Word2Vec 之 Skip-Gram 模型. 知乎
[^2]: 刘建平. word2vec原理. cnblogs[^3]: 王喆. 万物皆Embedding，从经典的word2vec到深度学习基本操作item2vec. 知乎
[^4]: 大海之中. Item2Vec笔记. 51CTO[^5]: 王喆. Embedding在深度推荐系统中的3大应用方向. 知乎
[^6]: rongzijing. 词向量怎么评估好坏[^7]: 王喆. 深度学习中不得不学的Graph Embedding方法. 知乎
[^8]: 黄昕等. 推荐系统与深度学习. 清华大学出版社
[^9]: 浅梦. LINE：算法原理，实现和应用. 知乎
[^10]: 王喆. 关于Node2vec算法中Graph Embedding同质性和结构性的进一步探讨. 知乎