《统计学习方法——第2章》
第2章: 感知机
感知机(perceptron)是二分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,去+1和-1二值。
感知机将输入空间中的实例划分为两类的分离超平面,属于判别模型。
学习一个统计学习方法都从第1章所说的三个要素出发:模型、策略、算法;
一、感知机模型
1、定义:什么是感知机?
简单来说,感知机就是下面一个函数f(x):
![]()
其中sign(x)是这样的函数:
通过上面可得,给定一个输入空间的实例,也就是给函数输入一个样本,感知机输出的结果要么是-1,要么是+1。对于二分类来说,比如预测一个样本是否合格,我们规定合格为+1,不合格为-1。这样就可以通感知机来实现了。
2、参数说明:
其中x是属于输入空间的实例,可以理解为输入的样本,是用一个向量来表示的。
w是感知机模型的参数,叫作权值或权值向量,也是一个向量来表示的。
b叫作偏置,也是一个向量来表示的。
3、感性理解什么是感知机?
假设输入的实例x的特征向量只有两个,人的身高和体重。通过感知机来判断其是否属于超重。要是超重的话就表示为+1,不超重就表示为-1。
将输入空间的全部实例在二维的坐标中画出来,假设以身高为X轴,体重为Y轴,那么全部的样本点就可以在二维坐标中表示出来了。
这个时候的感知机就是找到一条线,将全部的样本来区分开来。
比如在线的左边的样本就是表示+1,为超重;
在线的右边的样本就是表示为-1,为不超重,即合格;
如下图所示:
上面是两个特征向量的情况下,要是有三个特征向量的话,把全部的样本在三维空间中表示出来,这时感知机就是可以是一个片面了,用一个平面来将样本来区分开来。
4、对 w·x+b=0的理解;
我们说,统计学习方法的第一个要素就是找到一个合适的模型。对于感知机模型来说,它的假设空间是函数{f|f(x)=w·x+b},即是定义在特征空间中的所有线性分类模型或线性分类器;【注:这里的x,w,b都是向量,f(x)不是一元一次函数】;
对于线性方程 w·x+b=0:
对应于特征空间中的一个超平面S,其中w是超平面的法向量,b是超平面的截距,这个超平面将特征空间分为了两个部分,位于两部分的点(特征向量)分别被分为正、负两类。因此,超平面S称为分离超平面。如下所示: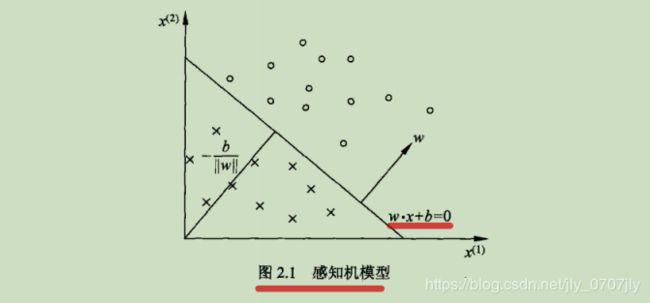
5、如何求得感知机模型?
求得感知机模型就是求得模型的参数w,b。当我么确定了模型之后,就可以选定合适的策略,加上实现的算法就可以求得了。
二、感知机学习策略
1、数据集的线性可分性
对于一个数据集T,如果存在某个超平面S(w·x+b=0)能够将数据集的正实例点和负实例点完全正确的划分到超平面的两侧,则层数据集T为线性可分数据集。
2、感知机学习策略
假设数据集T是线性可分的,感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。
为了找到一个学习策略,即定义一个损失函数并将损失函数极小化。
损失函数要是参数w,b的连续可导函数,这样的话易于优化损失函数。
感知机的损失函数:误分类点到超平面S的总距离。
三、感知机学习算法
感知机学习问题转化为求解损失函数式的最优化问题,最优化的方法是随机梯度下降法。
1、感知机学习算法的原始形式:
算法1:
解释:
当一个实例点被误分类,即位于分离超平面的错误一侧时,则调整w,b的值,使分离超平面向改误分类的一侧移动,以减少该误分类点与超平面间的距离。
【注】感知机学习算法由于采用不同的初始值或选取不同的误分类点,解可以不同。
2、算法的收敛性:
对于线性可分数据集感知机学习算法原始形式收敛,即经过有限不同次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。
【数学证明略:太多数学的公式了~~~。记住结果就好,就是线性可分的数据集T是存在一个将其完全划分的感知机模型的】
定理表明:误分类的次数k是有上界的,经过有限次搜索可以找到将训练数据完全正确分开的分离超平面。
上述也说了,对于不同的w和b的初始值或不同的误分类点的选择顺序,会得到不同的感知机,为了得到唯一的超平面,需要对分离超平面增加约束条件,这就是线性支持向量机。
3、感知机学习算法的对偶形式:
感知机学习算法的原始形式和对偶形式与支持向量机学习算法的原始形式和对偶形式相对应。
对偶形式的基本思想是,将w和b表示为实例x和标记y的线性组合的形式,通过求解其基本的系数而求得w和b。

