机器学习课程笔记【十三】- 独立成分分析
本节为吴恩达教授机器学习课程笔记第十三部份,独立成分分析(Independent Components Analysis,ICA),主要包括:ICA的动机,ICA的歧义问题,概率密度函数上的线性变换,ICA算法以及极大似然法得到的权重更新规则,三种降维技术FA、PCA、ICA的比较和sklearn实现。
与主成分分析类似,独立成分分析也希望找到一个能够表示数据的新基底,但是二者又存在很大的差别。一个典型的例子,n个人同时在一个房间说话,房间中放置的任何一个收音器都只能记录n个人重叠的声音,加入我们现在有n个不同的收音器,因为每个收音器距离说话的人的距离都不同,所以收音器记录的重叠的声音实际上是不同的,那么我们能否用这n个收音器的记录把n个说话者的声音分开?
我们将这一问题形式化,设想数据 s ∈ R n s\in R^n s∈Rn是由 n n n个独立的源合成的,我们观测到的数据为 x = A S x=AS x=AS,其中 A A A是一个未知的方阵称为混合矩阵,我们观测到的数据给出了这样一个数据集 { x ( i ) ; i = 1 , . . . , m } \{x^{(i)};i=1,...,m\} {x(i);i=1,...,m},我们的目标是从观测到的数据中还原 s ( i ) s^{(i)} s(i)。
对应于第一段的例子, s ( i ) s^{(i)} s(i)是一个 n n n维向量其中 s j ( i ) s_j^{(i)} sj(i)表示 i i i这个时间点说话人 j j j的声音, x ( i ) x^{(i)} x(i)也是一个 n n n维向量其中 x j ( i ) x^{(i)}_j xj(i)表示收音器 j j j在 i i i这个时间点的记录。
记 W = A − 1 W=A^{-1} W=A−1,称为分离矩阵,我们的目标变为找到 W W W从而根据 s ( i ) = W x ( i ) s^{(i)}=Wx^{(i)} s(i)=Wx(i)还原数据,为了记录方便,记 ω i T \omega^T_i ωiT表示矩阵 W W W的第 i i i行,这样:
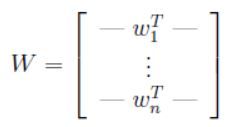
从而有 ω i ∈ R n \omega_i \in R^n ωi∈Rn,并且第 j j j个源可以通过计算 s j ( i ) = ω j T x ( i ) s_j^{(i)}=\omega_j^Tx^{(i)} sj(i)=ωjTx(i)来得到。
1. ICA算法的歧义问题
如果只给出 x ( i ) ’ s x^{(i)}’s x(i)’s而对源数据和混合矩阵缺乏先验知识,那么矩阵 A A A就会有歧义,不可能恢复。
令 P P P为一个 n × n n\times n n×n的置换矩阵,即 P P P的每一列只能有一个“1”,比如:
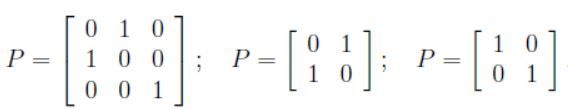
如果 z z z是一个向量,那么 P z Pz Pz就是另外一个包含 z ′ s z's z′s的坐标的置换版本的向量。仅给定 x ( i ) x^{(i)} x(i)’s并不能区分 W W W和 P W PW PW,也就是说源的置换的具有歧义的。
同样,也没有办法来正确的还原 ω i \omega_i ωi’s的缩放。例如,如果 A A A被 2 A 2A 2A替换,并且每一个 s ( i ) s^{(i)} s(i)就会被 ( 0.5 ) s ( i ) (0.5)s^{(i)} (0.5)s(i)替换,此时我们观测到的 x ( i ) = 2 A ⋅ ( 0.5 ) s ( i ) x^{(i)}=2A \cdot (0.5)s^{(i)} x(i)=2A⋅(0.5)s(i)未发生变化。更一般的,如果 A A A的某一行缩放因子为 α \alpha α,那么对应源的缩放因子为 1 / α 1/\alpha 1/α时,那么无法只根据 x ( i ) x^{(i)} x(i)’s来决定缩放情况。因此我们不能得到正确的源。但是在我们讨论的问题中,这种歧义其实影响不大,比如,对某个说话者的说话信号 s j ( i ) s_j^{(i)} sj(i)施加某个正的缩放因子 α \alpha α影响的仅仅是说话者说话的音量,同样正负符号也不影响, s j ( i ) 和 − s j ( i ) s_j^{(i)}和-s_j^{(i)} sj(i)和−sj(i)信号听起来一样。因此如果 ω i \omega_i ωi能够通过算法得到然后施加一个非0实缩放因子,对应分离出的源 s i = ω i T x s_i=\omega_i^Tx si=ωiTx也会包含相同的缩放因子,但是这对问题求解并无影响。
上述讨论中的情况是ICA算法唯一的模糊性来源,只要源 s i s_i si不是高斯分布。[接下来看看如果数据是高斯的,会有什么困难]设想这么一个例子,其中 n = 2 , s ∼ N ( 0 , I ) n=2,s\sim N(0,I) n=2,s∼N(0,I),其中 I I I是一个 2 × 2 2\times 2 2×2的单位矩阵。标准正态分布的密度函数的等值线是圆心在原点的圆,并且密度函数的图像中心对称。假设我们观测到某个 x = A s x=As x=As,其中 A A A是混合矩阵,那么得到的 x x x的分布也是高斯的,并且均值为0,协方差为 E [ x x T ] = E [ A s s T A T ] = A A T E[xx^T]=E[Ass^TA^T]=AA^T E[xxT]=E[AssTAT]=AAT,令 R R R为任意正交矩阵,也就是说 R R T = R T R = I RR^T=R^TR=I RRT=RTR=I,令 A ′ = A R A'=AR A′=AR,那么如果数据已经根据 A ′ A' A′混合,那么我们就会有 x ′ = A ′ s x'=A's x′=A′s, x ′ x' x′的分布也会是高斯,均值0,协方差为 E [ x ′ ( x ′ ) T ] = E [ A ′ s s T ( A ′ ) T ] = E [ A R s s T ( A R ) T ] = A R R T A T = A A T E[x'(x')^T]=E[A'ss^T(A')^T]=E[ARss^T(AR)^T]=ARR^TA^T=AA^T E[x′(x′)T]=E[A′ssT(A′)T]=E[ARssT(AR)T]=ARRTAT=AAT,也就是说无论混合矩阵是 A A A还是 A ′ A' A′,都会观测到数据来自一个 N ( 0 , A A T ) N(0,AA^T) N(0,AAT)的分布,这就没有办法来判别源使用的混合矩阵是哪一个了。即如果混合矩阵中有一个不能从数据中确定的旋转分量,那么就不能对数据进行还原。
综上所述,只要源数据不服从高斯分布,只要给出足够的数据,就可以将观测到的数据还原为 n n n个独立的源。
2. 密度函数上的线性变换
在推导ICA算法之前,我们先讨论一下在密度函数上做线性变换的效果。
设想我们有一个随机变量 s s s,它的密度函数为 p s ( s ) p_s(s) ps(s),为简单起见,令 s ∈ R s\in R s∈R表示一个实数,然后令随机变量 x = A s ( x ∈ R , A ∈ R ) x=As(x\in R,A\in R) x=As(x∈R,A∈R),令 p x p_x px表示 x x x的密度,那么如何求 p x p_x px呢?
令 W = A − 1 W=A^{-1} W=A−1,为了计算 x x x某个特定值的概率,看起来我们可以计算 s = W x s=Wx s=Wx,然后根据 p s p_s ps得出 p x ( x ) = p s ( W x ) p_x(x)=p_s(Wx) px(x)=ps(Wx),但是这并不正确,比如令 s ∼ U n i f o r m [ 0 , 1 ] s \sim Uniform[0,1] s∼Uniform[0,1],那么 s s s的概率密度 p s ( s ) = 1 { 0 ≤ s ≤ 1 } p_s(s)=1\{0 \leq s \leq 1\} ps(s)=1{0≤s≤1},令 A = 2 则 x = 2 s A=2则x=2s A=2则x=2s,显然 x x x在区间 [ 0 , 2 ] [0,2] [0,2]上服从均匀分布,可以给出 x x x的概率密度函数 p x ( s ) = ( 0.5 ) 1 { 0 ≤ s ≤ 2 } p_x(s)=(0.5)1\{0 \leq s \leq 2\} px(s)=(0.5)1{0≤s≤2},这与 p s ( W x ) p_s(Wx) ps(Wx)并不相等,因为 W = 0.5 = A − 1 W=0.5=A^{-1} W=0.5=A−1,正确的公式实际上是 p x ( x ) = p s ( W x ) ∣ W ∣ p_x(x)=p_s(Wx)|W| px(x)=ps(Wx)∣W∣。
更一般地,如果 s s s是一个概率密度为 p s p_s ps的向量值的分布,且存在一个可逆方阵 A A A使得 x = A s x=As x=As成立,那么 x x x的概率密度函数 ( W = A − 1 ) (W=A^{-1}) (W=A−1):
![]()
3. ICA算法
假定每一个源 s i s_i si的分布都是由概率密度函数 p s p_s ps给出,源 s s s的联合分布由下式给出:

也就是说把联合分布建模为边缘分布的乘积(因为各个源是互相独立的),根据我们之前的讨论, x = A s = W − 1 s x=As=W^{-1}s x=As=W−1s:

因为对于一个实数值随机变量 x x x,累积分布函数 F ( z 0 ) = P ( z ≤ z 0 ) = ∫ − ∞ z 0 p z ( z ) d z F(z_0)=P(z\leq z_0)=\int^{z_0}_{-\infty}p_z(z)dz F(z0)=P(z≤z0)=∫−∞z0pz(z)dz,同理 z z z的概率密度可以由分布函数求导得到 p ( z ) = F ′ ( z ) p(z)=F'(z) p(z)=F′(z)。
那么为了得到每一个 s i s_i si的密度,我们需要做的就是得到它的累积分布函数,累积分布函数必定是值域 [ 0 , 1 ] [0,1] [0,1]的单调增函数。根据之前的讨论,我们不能选择高斯分布的累积分布函数,因为ICA在服从高斯分布的数据上无效。我们可以选择一个缓慢从0增长到1的合理的默认函数sigmoid函数 g ( s ) = 1 / ( 1 + e − s ) g(s)=1/(1+e^{-s}) g(s)=1/(1+e−s),也就是有 p s ( x ) = g ′ ( s ) p_s(x)=g'(s) ps(x)=g′(s)。
方阵 W W W作为模型的参数,给定一个训练集 { x ( i ) ; i = 1 , . . . , m } \{x^{(i)};i=1,...,m\} {x(i);i=1,...,m},对数似然函数可以写为:
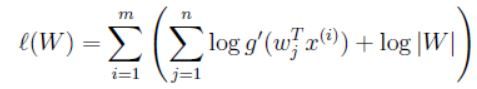
我们需要根据 W W W来最大化对数似然函数,通过求导并且利用 ▽ W ∣ W ∣ = ∣ W ∣ ( W − 1 ) T \bigtriangledown _W|W|=|W|(W^{-1})^T ▽W∣W∣=∣W∣(W−1)T,我们可以得到随机梯度更新规则,对于一个训练样本 x ( i ) x^{(i)} x(i),更新规则为:
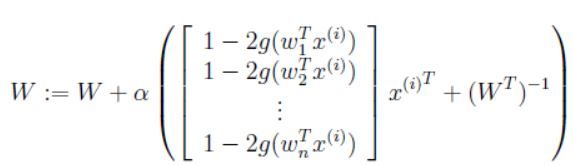
其中 α \alpha α为学习率,算法收敛之后,我们可以通过计算 s ( i ) = W x ( i ) s^{(i)}=Wx^{(i)} s(i)=Wx(i)还原源。
4. FA,PCA,ICA及其python实现
至此我们学习了三种数据降维技术,在因子分析技术中,变量按其相关性进行分组,即特定组内的所有变量之间具有高度相关性,但往往与其他组的变量之间相关性较低。在这里,每个组都被称为一个因子。与原始数据维度相比,这些因子的数量很少。但是,这些因子往往很难观察到。
from sklearn.decomposition import FactorAnalysis
# n_components将决定转换数据中的因子数量
FA = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)
主成分分析,可以帮助我们从现有的大量变量中提取一组新的变量。这些新提取的变量称为主成分,在PCA中:
- 主成分是原始变量的线性组合
- 提取主成分的方法是,第一主成分解释数据集中的最大方差
- 第二主成分试图解释数据集中的剩余方差,并与第一主成分不相关
- 第三主成分试图解释前两个主成分无法解释的方差等,以此类推
from sklearn.decomposition import PCA
# n_components将决定转换数据中的主要成分的数量
pca = PCA(n_components=4)
pca_result = pca.fit_transform(df[feat_cols].values)
我们添加到PCA技术中的每个额外维度获取模型中的方差越来越少。第一个部分是最重要的成分,其次是第二个成分,然后是第三个成分,依此类推。
谈到PCA不得不提SVD,SVD 相当于an implementation of PCA,避免了协方差矩阵的计算,其将原始变量分解为三个组成矩阵。它主要用于从数据集中删除冗余的特征。它使用特征值和特征向量的概念来确定这三个矩阵。
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=3, random_state=42).fit_transform(df[feat_cols].values)
独立成分分析(ICA)是基于信息理论的,也是最广泛使用的降维技术之一。PCA和ICA之间的主要区别在于PCA寻找不相关的因素,而ICA寻找独立因素。
如果两个变量不相关,则意味着它们之间没有线性关系。如果它们是独立的,则意味着它们不依赖于任何其他变量。例如,一个人的年龄与该人吃什么或他/她看多少电视无关。
该算法假设给定变量是一些未知潜在变量的线性混合。它还假设这些潜在变量是相互独立的,即它们不依赖于其他变量,因此它们被称为观察数据的独立成分。
from sklearn.decomposition import FastICA
ICA = FastICA(n_components=3, random_state=12)
X=ICA.fit_transform(df[feat_cols].values)
关于ICA和PCA,ICA认为观测信号是若干个统计独立的分量的线性组合,要做的是一个解混过程。而PCA是一个信息提取的过程,将原始数据降维,现已成为ICA将数据标准化的预处理步骤,能够大大降低ICA的计算量。
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]
![]()