python-指数分布介绍（scipy.stats.expon）
一、指数分布问题：
有一种品牌的路由器，据厂家统计知该路由器平均寿命是50000小时，现在有2个问题：
1、去年我买了一个这样的路由器，使用到现在已经8000小时了一点问题都没有，那我这台路由器还能用40000小时以上的概率是多少？
2、 我现在推荐邻居也买了一个这样的路由器，邻居这台路由器可以用40000小时以上的概率是多少？
二、 指数分布
泊松分布描述的是事件发生次数，而指数分布描述的是事件发生的时间间隔。
指数分布主要用于描述电子元器件的寿命，其为连续型分布，概率密度函数为：
分布函数为：
期望： 
， 方差： 
表示事件发生的频率，在这里路由器平均寿命是50000小时，那么可以认为路由器平均50000小时坏一次，那么路由器坏的频率是=1/50000。
此外，指数分布有一个十分重要的性质，无记忆性：
在上面问题中，路由器已使用时间与后续还能使用的时间无关，即我的路由器与邻居家的路由器后续使用寿命是没有差别的，即问题1和2的概率是一样的。
三、概率密度图
用python计算概率密度，可以直接使用公式计算，或者用scipy.stats.expon计算：
from scipy import stats
import math
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号
r = 1/50000
X = []
Y = []
for x in np.linspace(0, 1000000, 100000):
if x==0:
continue
# p = r*math.e**(-r*x) #直接用公式算
p = stats.expon.pdf(x, scale=1/r) #用scipy.stats.expon工具算,注意这里scale参数是标准差
X.append(x)
Y.append(p)
plt.plot(X,Y)
plt.xlabel("间隔时间")
plt.ylabel("概率密度")
plt.show()结果：
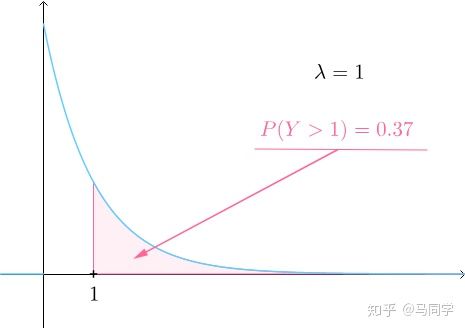
针对这个图该如何理解呢？连续型随机变量的概率密度在某个点的概率密度并不是在这一点发生的概率。这里引用一张图
这张图说明事件发生的时间间隔大于1的概率是0.37，那么时间间隔小于1的概率是0.63，这一点用下面的累积概率分布来看更直观。
四、累积概率分布（查表）
累积概率用stats.expon.cdf(x, scale=1/r)计算，当然也可以用公式计算。
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号
r = 1/50000
X = []
Y = []
for x in np.linspace(0, 1000000, 100000):
if x==0:
continue
p = stats.expon.cdf(x, scale=1/r) #用scipy.stats.expon工具算,注意这里scale参数是标准差
X.append(x)
Y.append(p)
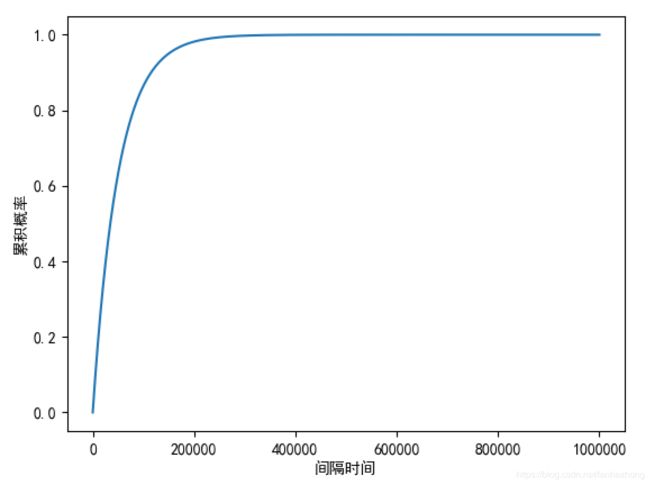
plt.plot(X,Y)
plt.xlabel("间隔时间")
plt.ylabel("累积概率")
plt.show()结果：
用累积概率查表x=40000的值:
p = stats.expon.cdf(40000, scale=50000)
print(p)结果是：0.5506710358827784
也就是说事件发生时间间隔小于40000的概率是0.55067，那么问题1和2路由器在40000小时内坏的概率是0.55067，相应的可以使用40000小时以上的概率是1-0.55067=0.44933。
五、再来2个问题
医院平均每小时出生3个婴儿，问：
1、接下来15分钟有婴儿出生的概率是多少？
2、在接下来的15~30分钟内有婴儿出生的概率是多少?
问题1：
这里婴儿出生频率
，查表
p = stats.expon.cdf(15/60, scale=1/3)
print(p)结果：0.5276334472589853
表明在15分钟内有婴儿出生的概率是0.5276。
注意这里只是表明有婴儿出生的概率是0.5276，并没有指定有多少个婴儿出生，更没有表明有1个婴儿出生的概率是0.5276。
问题2：
由于指数分布是无记忆的，在接下来的15~30分钟内一共15分钟，有婴儿出生的概率与问题1概率一样，都是0.5276。
有些人不理解这个意思，错误的用cdf(30/60)-cdf(15/60)
p15 = stats.expon.cdf(15/60, scale=1/3)
p30 = stats.expon.cdf(30/60, scale=1/3)
print(p30-p15)结果：0.2492363925925849
这个结果并不表明在接下来的15~30分钟内有婴儿出生的概率。
而是表明在0~15分钟内没有婴儿出生并且在15~30分钟内有婴儿出生的概率是0.2492，或者表明接下来出生的第一个孩子时间在15~30分钟的概率是0.2492。