数据结构算法入门--链表
2019 年第 76 篇文章,总第 100 篇文章
本文大约 3200 字,阅读大约需要 10 分钟
数据结构算法系列:
数据结构算法入门系列第三篇--链表,链表也是非常常见的数据结构,面试过程中也会经常考到相关的题目。
本文首先介绍链表的基本情况,比如单向链表、双向链表等,然后会介绍一些技巧。
今日推荐阅读:
链表也是一个非常常见的数据结构,和数组相比,它不需要连续的内存空间,对内存的要求不高。
链表结构非常多,这里介绍常见的三种结构:单链表、双向链表和循环链表。
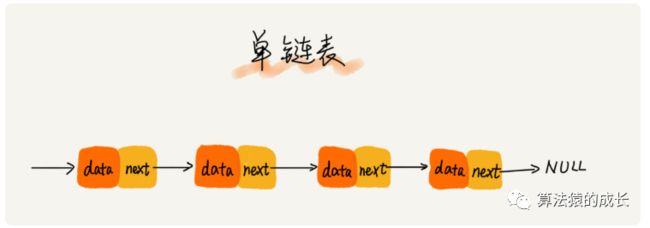
单链表
链表是通过指针将一组零散的内存块串联在一起,其中,内存块称为链表的 "结点",如下图所示,结点分为两个部分,存储数据以及记录下一个结点的地址的指针,这个指针也称为后继指针 next。
从图中可以看到有两个结点比较特殊,头结点和尾结点。其中,头结点保存链表的基地址,而尾结点的指针指向一个空地址 NULL。
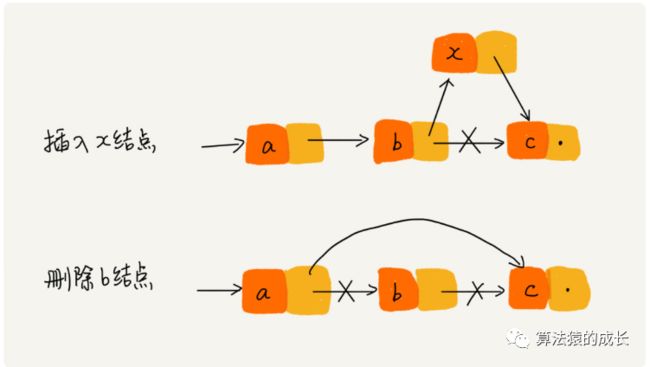
链表也是支持查找、插入和删除操作的,对于链表的插入和删除操作,可以如下图所示,插入和删除操作,其实仅仅需要改变相邻结点的指针,对应的时间复杂度是 O(1)。
当然了,有利就有弊,和数组可以实现快速随机访问操作相反,链表这操作需要 O(n) 的时间复杂度。因为链表因为不是连续的内存块,所以不能根据首地址和下标,通过寻址公式计算得到目标位置的内存,只能从首结点开始遍历每个结点,直到找到目标结点。
循环链表
介绍完单链表,第二个介绍的就是升级版--循环链表。
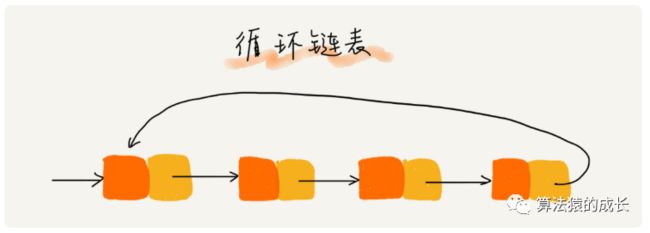
循环链表,和单链表的区别主要是**尾结点指向的是链表的头结点,**如下图所示,因此循环链表构成一个环,因此称为循环链表。
循环链表的优点就是从链尾到链头比较方便。它适合解决具有环型结构特点的数据,比如著名的约瑟夫问题[^1]。
双向链表
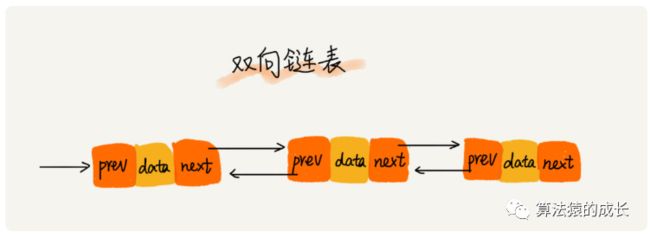
第三个升级版--双向链表,也是比较常用的一种链表结构。它的特点就是每个结点包含两个指针,分别指向前一个结点和后一个结点,也就是两个方向,所以称为双向链表,如下图所示:
相比于单链表,因为多一个指针,所以双向链表会占用更多的内存空间,但它也更加灵活,此外,它可以在 O(1) 时间复杂度的情况下找到前驱结点,在某些情况下,插入、删除等操作会比单链表更加简单和高效。
尽管介绍单链表的插入和删除操作,提到其时间复杂度是 O(1) ,但这里是有一个前提的,就是仅仅插入或者删除操作,并没有考虑查找的时间,如果结合查找到结点并插入或者删除操作,那么时间复杂度应该是 O(n) 。
而双向链表可以在需要查找结点的前驱结点时候,比单链表更加高效。
这也是一个重要的设计思想--空间换时间。当内存空间充足的时候,如果追求速度,可以采用一些时间复杂度相对比较低,但空间复杂度相对比较高的算法或者数据结构;当然如果内存空间不足,那就反向考虑,时间换空间的设计思路。
比较经典的例子就是缓存,事先将数据加载在内存中,尽管会比较耗费内存空间,但查找速度就大大提高了。
总结一下,对于执行较慢的程序,可以采用空间换时间的思路优化;而消耗过多内存的程序,可以通过时间换空间的思路来优化。
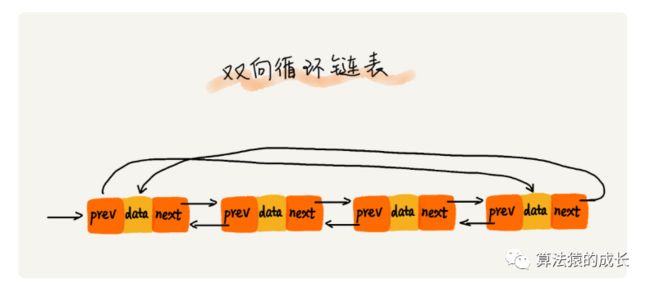
双向链表还可以和循环链表结合--双向循环链表,如下图所示:
链表 vs 数组性能大比拼
和数组进行对比,两者在插入、删除、随机访问操作的时间复杂度是正好相反的,如下表所示:
| 时间复杂度 | 数组 | 链表 |
|---|---|---|
| 插入&删除 | O(n) | O(1) |
| 随机访问 | O(1) | O(n) |
当然,并不能仅仅通过时间复杂度来对比数组和链表,实际应用需要考虑更多的因素。
数组的优缺点:
-
优点:简单易用,采用连续的内存空间,可以借助 CPU 的缓冲机制,预读数组中的数据,访问效率更高;
-
缺点:大小固定,一经声明就需要占用整块连续内存空间,占用空间过大和过小都有各自的问题。
而链表的优缺点其实刚好相反:
-
优点:没有限制大小,天然支持动态扩容;
-
缺点:占用的内存并不是连续存储,对 CPU 缓存不友好,无法有效预读,访问效率不高。
链表技巧
1. 理解指针或引用的含义
有些语言,比如 C 语言,有指针的概念;但有些语言没有指针,取而代之的是“引用”的概念,比如 Python。不过,这两者表示的意思都一样,都是存储所指对象的内存地址。
实际上,对于指针或者引用的理解,只需要记住这句话:
将某个变量赋值给指针,实际上就是将这个变量的地址赋值给指针,也可以说,指针存储了这个变量的内存地址,指向了这个变量,可以通过指针来找到这个变量。
用代码举例说明,比如:p->next= q ,这段代码表示 p 结点的 next指针指向了 q 结点的内存地址。
更复杂点的例子,p->next=p->next->next ,这段代码表示 p 结点的 next 指针存储了 p 结点的下下一个结点的内存地址。
2. 警惕指针丢失和内存泄露
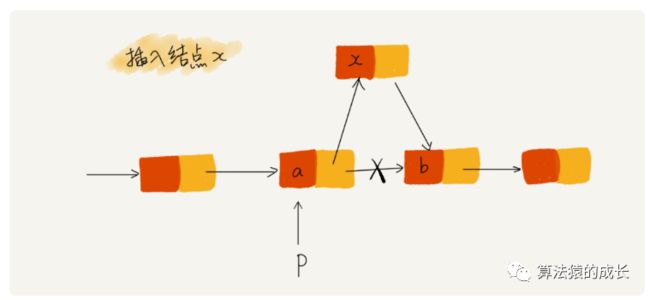
对于链表,最重要的是确保指针指向正确的结点,一旦写错,就会导致丢失指针,那么这种情况一般是怎么发生的呢,下面给出一个单链表插入操作的例子,如下图所示:
上述例子是希望在结点 a 和 b 之间插入新的结点 x,假设当前指针 p 指向结点 a,如果采用下面的代码,那么就会发生指针丢失和内存泄露。
p->next = x; // 将 p 的 next 指针指向 x 结点;
x->next = p->next; // 将 x 的结点的 next 指针指向 b 结点;这段代码是这样执行的:
-
首先指针 p->next 会指向结点 x;
-
接着,x->next 执行 p->next,也就是说 x->next 指向结点 x,也就是结点 x 自己构成一个闭环了,那么后续结点都无法访问了。
正确的代码,其实是将上述代码交换执行顺序,即先让 x->next 指向 p->next,也就是结点 b,然后再将 x 赋值给 p->next。
所以,插入结点,需要注意操作的顺序;而删除结点,对于没有内存管理的编程语言,需要手动释放内存空间。
3. 利用哨兵简化实现难度
正常的单链表的插入操作,代码实现如下所示,
new_node->next = p->next
p->next = new_node但如果是在链表首部插入新的结点,则必须单独处理:
if head == null:
head = new_node同理对于删除结点操作,代码如下所示,也就是对链表最后一个结点需要特殊处理。
if head->next == null:
head = null
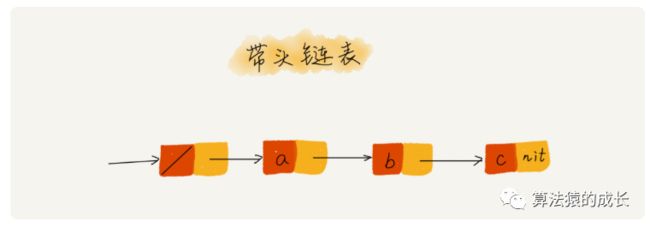
p->next = p->next->next那么是否有办法可以不用单独处理呢,这里就可以采用哨兵,即引入哨兵结点,在任何时候,不管链表是否为空,head 指针都会一直指向这个哨兵结点。这种带有哨兵结点的链表叫做带头链表,没有带的则是不带头链表。如下所示:
4. 重点留意边界条件处理
通常在边界或者异常情况下,最容易产生 Bug。对于链表,也不例外,在写代码过程和写完后,都需要检查代码添加是否考虑全面,以及代码在边界条件下能否正常运行。
通常用于检查链表代码是否正确的边界条件有这几个:
-
如果链表为空,是否能正常工作?
-
如果链表只有一个结点,是否可以正常工作?
-
如果链表包含两个结点,是否可以正常工作?
-
代码逻辑在处理头结点和尾结点的时候,是否可以正常工作?
当然,边界条件并不局限上述这些,不同场景,还有特点的边界条件。
5. 举例画图,辅助思考
对于复杂的链表操作,比如单链表反转,可以采用举例法和画图法进行辅助。
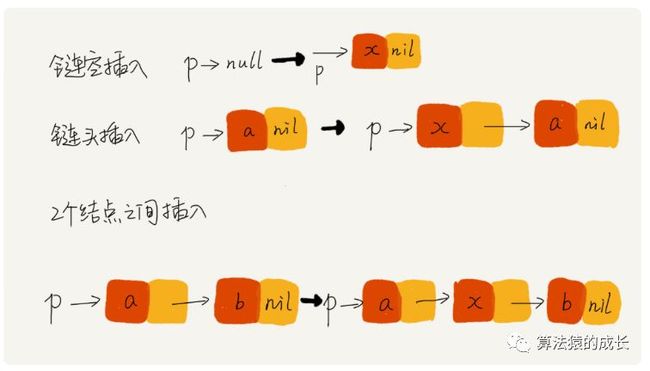
比如,对于链表插入的操作,如下图给出不同情况下,插入前后的链表变化:
通过举例和画图,会非常直观形象的了解应该如何用代码实现相应的操作。
6. 多写多练,没有捷径
最重要的还是多写多练,不断总结错误。
参考:
-
极客时间的数据结构与算法之美课程
欢迎关注我的微信公众号--算法猿的成长,或者扫描下方的二维码,大家一起交流,学习和进步!