游戏跨场景寻路-基于egret（白鹭）的实现

游戏跨场景寻路-基于egret（白鹭）的实现

本文转自：https://blog.csdn.net/u013052238/article/details/83052350

参考网址：

• 原理性讲解：https://www.toutiao.com/a6540828594954830340/

• 基于as3的代码：https://blog.csdn.net/sjt223857130/article/details/77199601

• 堆优化理解：https://www.cnblogs.com/jason2003/p/7222182.html

• 基于C++的代码：https://blog.csdn.net/qq_35644234/article/details/60870719

• 相关注释：https://www.cnblogs.com/zzzPark/p/6060780.html

• 代码参考：https://blog.csdn.net/u013052238/article/details/80273042

此文主要讲跨地图间的最短路径，AI 寻路参考 A* 算法：https://blog.csdn.net/u013052238/article/details/53375860，以及A*算法的优化：https://blog.csdn.net/u013052238/article/details/78126019

---

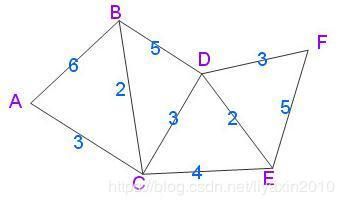
一、以下图作为多地图顶点：

---

二、地图数据字典配置简要设置如下：

{
    "A": {
        "B": {"len": 6},
        "C": {"len": 3}
    },
    "B": {
        "A": {"len": 6},
        "C": {"len": 2},
        "D": {"len": 5}
    },
    "C": {
        "A": {"len": 3},
        "B": {"len": 2},
        "D": {"len": 3},
        "E": {"len": 4}
    },
    "D": {
        "B": {"len": 5},
        "C": {"len": 3},
        "E": {"len": 2},
        "F": {"len": 3}
    },
    "E": {
        "C": {"len": 4},
        "D": {"len": 2},
        "F": {"len": 5}
    },
    "F": {
        "D": {"len": 3},
        "E": {"len": 5}
    }
}

---

三、为地图设置Vo类，这里简单设置MapVo类，带有mapId属性（如上的A~F顶点）

 
/**顶点地图数据 */
class MapVo {
	public mapID: string = "";
}

---

四、新建地图数据类存储对应矩阵的相关数据，这里设置MGraph（邻接矩阵）类:

/**邻接矩阵 */
class MGraph {
	/**邻接矩阵数组 */
	public edgeMatrixList: number[][];
	/**顶点数 */
	public pointNumber: number;
	/**存放顶点信息 */
	public mapDataList: MapVo[];
 
	public constructor() {
		this.edgeMatrixList = [];
		this.mapDataList = [];
		this.pointNumber = 0;
	}
}

---

五、新建类CrossMap初始化地图数据：

class CrossMap {
 
	/**地图配置表数据 */
	private gMapSource: any;
	/**INFINITY: 无穷大 */
	private INFINITY: number = 999999;
	/**邻接矩阵数据 */
	private gMGraph: MGraph;
 
	public constructor(mapSourcelist: any) {
		this.gMapSource = mapSourcelist;
 
		this.gMGraph = new MGraph();
		this.gMGraph.pointNumber = Object.keys(this.gMapSource).length;
 
		for (let point in this.gMapSource) {
			let _mapVo: MapVo = new MapVo();
			this.gMGraph.mapDataList.push(_mapVo);
			_mapVo.mapID = point;
		}
 
		//建立图的邻接矩阵
		for (let i: number = 0; i < this.gMGraph.pointNumber; i++) {
			if (!this.gMGraph.edgeMatrixList[i]) {
				this.gMGraph.edgeMatrixList[i] = [];
			}
			for (let j: number = 0; j < this.gMGraph.pointNumber; j++) {
				//计算i到j的权值
				let mapI: string = this.gMGraph.mapDataList[i].mapID;
				let mapJ: string = this.gMGraph.mapDataList[j].mapID;
				if (this.gMapSource[mapI]) {
					if (this.gMapSource[mapI][mapJ]) {				//判断地图I到地图J能不能走通
						this.gMGraph.edgeMatrixList[i][j] = this.gMapSource[mapI][mapJ].len;//权值设为配置
						// this.gMGraph.edgeMatrixList[i][j] = 1;	//默认给权值都为1
						continue;
					}
				}
				this.gMGraph.edgeMatrixList[i][j] = this.INFINITY;
			}
		}
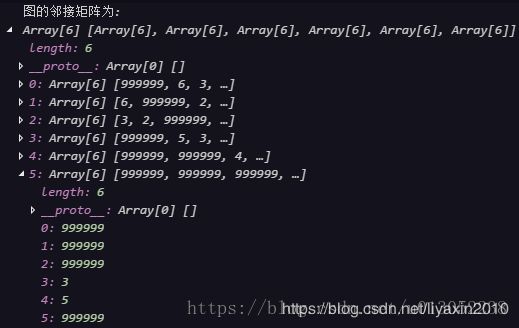
		console.log("图的邻接矩阵为:", this.gMGraph.edgeMatrixList);
 
        /**导出路径数据 */
		this.exportPath();
	}
 
	/**保存搜索完后所有相关的路径字典 */
	private allPathDic: { [mapId: string]: string[] } = {};
 
    private exportPath(){
        ......
    }
}

获得地图的邻接矩阵数据如下：

---

六、开始迪杰斯特拉算法查找各个点距离其他点的最短路径：

/**保存所有路径字典 */
private allPathDic: { [mapId: string]: string[] } = {};

private exportPath() {
    let time = egret.getTimer();
    let pointNum: number = this.gMGraph.pointNumber;
    for (let i: number = 0; i < pointNum; i++) {
        this.dijkstra(i, this.gMGraph);
    }
    console.log("跨地图数据生成耗时：" + (egret.getTimer() - time) + "ms");
}

private dijkstra(sourcePoint: number, _MGraph: MGraph) {
    let dist: number[] = [];					//从原点sourcePoint到其他的各定点当前的最短路径长度
    let path: number[] = [];					//path[i]表示从原点到定点i之间最短路径的前驱节点
    let selectList: number[] = [];  			//选定的顶点的集合
    let minDistance, point = 0;

    for (let i = 0; i < _MGraph.pointNumber; i++) {
        dist[i] = _MGraph.edgeMatrixList[sourcePoint][i];       		//距离初始化
        selectList[i] = 0;                        						//selectList[]置空  0 表示 i 不在selectList集合中
        if (_MGraph.edgeMatrixList[sourcePoint][i] < this.INFINITY) {   //路径初始化
            path[i] = sourcePoint;
        } else {
            path[i] = -1;
        }
    }
    selectList[sourcePoint] = 1;                  				//原点编号sourcePoint放入selectList中
    path[sourcePoint] = 0;
    for (let i = 0; i < _MGraph.pointNumber; i++) {             //循环直到所有顶点的最短路径都求出
        minDistance = this.INFINITY;                    		//minDistance置最小长度初值
        for (let j = 0; j < _MGraph.pointNumber; j++)        	//选取不在selectList中且具有最小距离的顶点point
            if (selectList[j] == 0 && dist[j] < minDistance) {
                point = j;
                minDistance = dist[j];
            }
        selectList[point] = 1;                       		 	//顶点point加入selectList中
        for (let j = 0; j < _MGraph.pointNumber; j++)        	//修改不在selectList中的顶点的距离
            if (selectList[j] == 0)
                if (_MGraph.edgeMatrixList[point][j] < this.INFINITY && dist[point] + _MGraph.edgeMatrixList[point][j] < dist[j]) {
                    dist[j] = dist[point] + _MGraph.edgeMatrixList[point][j];
                    path[j] = point;
                }
    }
    this.putBothpath(_MGraph, dist, path, selectList, _MGraph.pointNumber, sourcePoint);//获取路径
}

private putBothpath(_MGraph: MGraph, dist: number[], path: number[], selectList: number[], pointNumber: number, sourcePoint: number) {
    for (let i = 0; i < pointNumber; i++) {
        if (selectList[i] == 1 && dist[i] < this.INFINITY) {
            /**路径点列表 */
            let pathVexsList: string[] = [];
            pathVexsList.push(_MGraph.mapDataList[sourcePoint].mapID);	//起点
            this.findPath(_MGraph, path, i, sourcePoint, pathVexsList);
            pathVexsList.push(_MGraph.mapDataList[i].mapID);			//终点

            /**测试 */
            let pathStr: string = "";
            for (let j: number = 0; j < pathVexsList.length; j++) {
                pathStr += pathVexsList[j];
                if (j != pathVexsList.length - 1) {						//不是结尾就加间隔符
                    pathStr += "-";
                }
            }
            /**测试 */

            let _pathKey: string = _MGraph.mapDataList[sourcePoint].mapID + "-" + _MGraph.mapDataList[i].mapID;
            if (!this.allPathDic[_pathKey]) {							//不存在

                this.allPathDic[_pathKey] = pathVexsList;
            }
            console.log("从 " + _MGraph.mapDataList[sourcePoint].mapID + " 到 " + _MGraph.mapDataList[i].mapID + " 的最短路径长度为: " + dist[i] + "\t 路径为: " + pathStr);
        }
        else {
            console.log('从 ' + _MGraph.mapDataList[sourcePoint].mapID + ' 到 ' + _MGraph.mapDataList[i].mapID + ' 不存在路径      ');
        }
    }
}

private findPath(_MGraph: MGraph, path: number[], i: number, sourcePoint: number, pathVexsList: string[]) {  //前向递归查找路径上的顶点
    let point;
    point = path[i];
    if (point == sourcePoint) return;    								//找到了起点则返回
    this.findPath(_MGraph, path, point, sourcePoint, pathVexsList);    	//找顶点point的前一个顶点sourcePoint
    pathVexsList.push(_MGraph.mapDataList[point].mapID);
}

查找得到路径存如下：

从 A 到 A 不存在路径           
从 A 到 B 的最短路径长度为: 5	 路径为: A-C-B     
从 A 到 C 的最短路径长度为: 3	 路径为: A-C     
从 A 到 D 的最短路径长度为: 6	 路径为: A-C-D     
从 A 到 E 的最短路径长度为: 7	 路径为: A-C-E     
从 A 到 F 的最短路径长度为: 9	 路径为: A-C-D-F
     
从 B 到 A 的最短路径长度为: 5	 路径为: B-C-A     
从 B 到 B 不存在路径           
从 B 到 C 的最短路径长度为: 2	 路径为: B-C     
从 B 到 D 的最短路径长度为: 5	 路径为: B-D     
从 B 到 E 的最短路径长度为: 6	 路径为: B-C-E     
从 B 到 F 的最短路径长度为: 8	 路径为: B-D-F 
    
从 C 到 A 的最短路径长度为: 3	 路径为: C-A     
从 C 到 B 的最短路径长度为: 2	 路径为: C-B     
从 C 到 C 不存在路径           
从 C 到 D 的最短路径长度为: 3	 路径为: C-D     
从 C 到 E 的最短路径长度为: 4	 路径为: C-E     
从 C 到 F 的最短路径长度为: 6	 路径为: C-D-F 
    
从 D 到 A 的最短路径长度为: 6	 路径为: D-C-A     
从 D 到 B 的最短路径长度为: 5	 路径为: D-B     
从 D 到 C 的最短路径长度为: 3	 路径为: D-C     
从 D 到 D 不存在路径           
从 D 到 E 的最短路径长度为: 2	 路径为: D-E     
从 D 到 F 的最短路径长度为: 3	 路径为: D-F  
   
从 E 到 A 的最短路径长度为: 7	 路径为: E-C-A     
从 E 到 B 的最短路径长度为: 6	 路径为: E-C-B     
从 E 到 C 的最短路径长度为: 4	 路径为: E-C     
从 E 到 D 的最短路径长度为: 2	 路径为: E-D     
从 E 到 E 不存在路径           
从 E 到 F 的最短路径长度为: 5	 路径为: E-F  
 
从 F 到 A 的最短路径长度为: 9	 路径为: F-D-C-A     
从 F 到 B 的最短路径长度为: 8	 路径为: F-D-B     
从 F 到 C 的最短路径长度为: 6	 路径为: F-D-C     
从 F 到 D 的最短路径长度为: 3	 路径为: F-D     
从 F 到 E 的最短路径长度为: 5	 路径为: F-E     
从 F 到 F 不存在路径

---

参考

• 游戏跨场景寻路】基于egret（白鹭）的游戏地图跨场景寻路功能的实现

• 游戏里的跨地图寻路算法-https://blog.csdn.net/u013052238/article/details/80273042

• 图的寻路算法-https://blog.csdn.net/qq_19782019/article/details/82624478