通过python理解相速度和群速度

从物理学的机制出发，波动模型相对于光线模型，显然更加接近光的本质；但是从物理学的发展来说，波动光学旨在解决几何光学无法解决的问题，可谓光线模型的一种升级。从编程的角度来说，波动光学在某些情况下可以简单地理解为在光线模型的基础上，引入一个相位项。

波动模型

一般来说，三个特征可以确定空间中的波场：频率、振幅和相位，故光波场可表示为：

$$E=Acos(\omega t-kr)$$

其中，$A$为振幅，$\omega =2\pi f=\frac{2\pi }{T}$为角频率，$k=\frac{2\pi }{\lambda }$，为波数。由上式可知，当时间固定时，光在传播方向上有一个正弦波的外形；而对于空间中任意一点，沿着振幅方向则进行简谐运动。

其中，振幅、波数以及空间位置均为矢量，当坐标比较混乱的时候，也可以写成$E=Acos(\omega t-kr)$；有时为了计算方便，也可以写成指数形式

$$E=A{e}^{-i(\omega t-kr)}$$

对于平面波来说，其发散角为0，即光场中的所有点，都具有统一的传播方向，且振幅相等。设其传播方向为$z$，则可写为

$$E=Acos(\omega t-kz)$$

球面波则相对复杂，令$r$为空间中任意一点到点光源的距离，则对于$a、b$两点来说，其单位面积的光通量之比为$\frac{I_a}{I_b}=\frac{r_b^2}{r_a^2}$，则振幅之比为$\frac{E_b}{E_a}=\frac{r_a}{r_b}$。这说明球面波振幅反比于波阵面到光源距离，即

$$E=\frac{A}{r}{e}^{-i(\omega t-kr)}$$

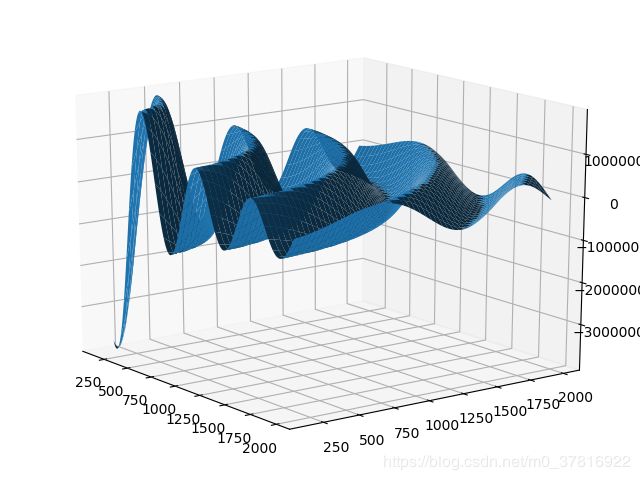
通过截取$xOz$平面，假设光波长为532nm,则可以画出这一截面处的光波振幅图。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
z = np.arange(15,200)*10    #单位为nm
x = np.arange(15,200)*10
x,z = np.meshgrid(x,z)      #创建坐标系
E = 1/np.sqrt(x**2+z**2)*np.cos(2*np.pi*np.sqrt(x**2+z**2)/(532*1e-9))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x,z,E)
plt.show()

其结果如图所示

相速度

经典的光波公式$E=Acos(\omega t-kr)$表示一个在空间中沿着一个方向传播的简谐波。如果现有多个频率相同的光波共同传播，那么由于不同光波之间可能存在相位差，虽然在任意一点上仍旧有着简谐运动的形式，但在任意时刻，其波峰波谷的位置显然不同。故可以写为

$$E=A(\mathbf{r})\cos (\omega \mathbf{t}-\mathbf{g}(\mathbf{r}))$$

指数形式为

$$E=A(\mathbf{r}){\mathbf{e}}^{\mathbf{i}\mathbf{g}(\mathbf{r})}{\mathbf{e}}^{-\mathbf{i}\omega \mathbf{t}}$$

其中，$g(r)$为常数，被称为等相位面，等相面并不重合的光波叫做非均匀波，即非均匀波可能在空间上不具备可计算的周期性。除非$\omega t-g(\mathbf{r})$的全微分为0，即$\omega dt-\text{grad}g\text{d}\mathbf{r}=0$。

$$\to \frac{\text{d}\mathbf{r}}{\text{d}t}=\frac{\omega }{\text{grad}g}$$

当$\mathbf{r}$的方向垂直于等相面时，上式数值最小，为

$$v_p(\mathbf{r})=\frac{\omega }{|\text{grad}\mathbf{g}|}$$

该式表示各等相位面前进的速度，为$\text{相速度}$。

群速度

对于平面波来说，$g(\mathbf{r})=\mathbf{k}\cdot \mathbf{r}-\delta$，则

$$v_p=\frac{\omega }{k}=\frac{c}{\sqrt{\epsilon \mu }}$$

当光波是由一群频率不同的光的叠加时，相速度便难以衡量光束的传播特性，也几乎是不可测的。而真实的光波往往是不同频率单色波的叠加

$$E(\mathbf{r},t)={\int }_0^{\infty }{A}_{\omega }(\mathbf{r})[\omega t-g_{\omega }(\mathbf{r})]$$

对于两个平面单色波来说，如果二者频率和相位都比较相近，振幅相同，且都沿着$z$轴传播，则对振幅进行归一化，上式可以简化为

$$\begin{array}{rl}\frac{E(z,t)}{a}=& \cos (\omega t-kz)+\cos [(\omega +\delta \omega )t-(k+\delta k)z]\\ \to & e^{-i(\omega t-kz)}+e^{-i[(\omega +\delta \omega )t-(k+\delta k)z]}\\ =& 2\cos [\frac{1}{2}(t\delta \omega -z\delta k)]e^{-i(\bar{\omega }t-\bar{k}z)}\\ \to & 2\cos [\frac{1}{2}(t\delta \omega -z\delta k)]\cos (\bar{\omega }t-\bar{k}z)\\ \text{其中}& \bar{\omega }=\omega +\frac{1}{2}\delta \omega ,\bar{k}=k+\frac{1}{2}\delta k\end{array}$$

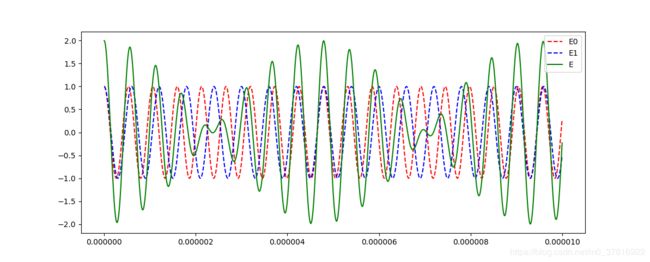
假设两列波的波长分别为532nm和600nm，则在同一时刻，不同位置处的光波振幅可通过python画出

def wavePacket(d = [532e-9,600e-9]):
    d = np.array(d)
    k = 2*np.pi/d           #波数
    dk = k[0]-k[1]          #波数差
    bk = k[1]+dk/2          #平均波数

    z = np.arange(10000)/1e9  #位置为0到10um

    E0 = np.cos(-k[0]*z)
    E1 = np.cos(-k[1]*z)
    E = E0+E1
    #E = 2*np.cos(-dk/2*z)*np.cos(-bk*z)

    fig = plt.figure()
    plt.plot(z,E0,'--',color='red',label='E0')
    plt.plot(z,E1,'--',color='blue',label='E1')
    plt.plot(z,E,'-',color='green',label='E')
    plt.legend()
    plt.show()

可见每间隔一段距离或者时间就会出现一个比较大的振幅，其极大间隔可以通过表达式求出

$$\delta t=\frac{2\pi }{\bar{\omega }}\delta z=\frac{2\pi }{\bar{k}}$$

则定义

$$v_g=\frac{\delta z}{\delta t}=\frac{\bar{\omega }}{\bar{k}}$$

为群速度，表示波包的传播速度。