【算法】蓝桥杯dfs深度优先搜索之图连通总结
前言
上两篇文章 → 《【算法】蓝桥杯dfs深度优先搜索之排列组合总结》
→ 《【算法】蓝桥杯dfs深度优先搜索之凑算式总结》
为了重申感谢之意,第三次声明下文的大部分灵感均来自于【CSDN】梅森上校《JAVA版本:DFS算法题解两个例子(走迷宫和求排列组合数)》
强烈推荐大家去上面那篇文章看看,写的很好。
下面我会列出蓝桥杯第七届B组省赛第6题、第7题,第九届第9题,共3道题。
因为他们都是:图连通问题。
正文
【第零道题】
我在第一篇文章“凑算式”中讲到的dfs套模板就是- 设数组
- 定义dfs()方法
- 递归结束条件
- for循环搜索
我在第二篇文章“排列组合”中重点说出的是dfs(arg1,arg2,…)方法不是只能传一个参数,而是有传多个参数的情况的。这是对上面那套模板的第2条的改变。
那么对于第三篇也就是现在这篇文章“图连通”的这道迷宫问题,我要重点说明的是上面那套模板的第4条,也就是对for循环搜索的改变。
这是一道走迷宫的题。梅森上校的那篇文章中讲解的很明白,我给简化一下,就是下面这个,0表示通行,1表示障碍物,问如何走出迷宫并输出路径和最短路径:
进 → [0 0 0]
[0 1 0]
[0 0 0] → 出
第一点我们还是要设一个数组a[],不过至于数组大小是多少我们并不知道,因为到底是怎么走的我们现在还没搜索出来,所以我们需要一个动态数组,C++中经常使用Vector向量,Java中也有相同的实现,但是再加考虑,我们需要同时存储(x,y)一对坐标,根据梅森上校代码中写的,我们干脆直接用一个字符串把它们拼起来就行了。
public static String path = "";
因为我们要找一条路径,所以dfs方法需要传入两个坐标和一个地图,这就是这类问题的套路
public static void dfs(int x, int y, int[][] map)
结束条件分四种情况,不要嫌多,这都是套路,见过一遍就能记住,前三个结束条件如下:
// 矩阵的大小
int m=map.length;
int n=map[0].length;
// 结束条件
if(x < 0 || y < 0) // 因为待会搜索的时候有减操作,所以有可能为负数“越界”
return;
if(x > m-1 || y > n-1) // 因为待会搜索的时候有加操作,所以有可能为正数越界
return;
if(map[x][y] == 1) // 遇到障碍物,走不通
return;
上面三个结束条件可以合在一起
if(x < 0 || y < 0 || x > m-1 || y > n-1 || map[x][y] == 1)
return;
第四个结束条件就是走到出口了,我们需要记录下来出口的坐标,并将这条通路的所有坐标都打印出来。
if(x == m-1 && y == n-1) { // 抵达出口
// 拼接出口坐标
path = path + "(" + x + "," + y + ")";
list.add(path); // 将所有通路加入到list中
//这里一定要return,回溯尝试下一条路
return;
}
接下来就是搜索了,我们在以前的for循环中,往往会做个标记,然后记录当前值,再然后才是递归下一个条件。在这里同样也需要标记一下,然后记录当前值,再然后进行递归,与以往不同的是,不在需要for循环了,而是四个方向的递归。看下面的代码,第一次见这样的代码记不住没关系,因为你脑中的神经元从未建立过如此连接,见多了就好了:
// 搜索
// 在搜寻下一个方向之前,先把当下的一些值记录下来
String temp = path;
path = path + "(" + x + "," + y + ")" + "→"; // 记录路线
map[x][y] = 1; // 将走过的路标记为1
// 向四个方向搜索,方向可以任意排列
dfsMap(x, y + 1, map); // 向右搜索
dfsMap(x + 1, y, map); // 向下搜索
dfsMap(x, y - 1, map); // 向左搜索
dfsMap(x - 1, y, map); // 向上搜索
map[x][y] = 0;// 恢复标记
path = temp; // 回溯路径
【完整代码】
package com.lanqiao.往年真题;
import java.util.ArrayList;
public class 走迷宫dfs字符串 {
public static String path = "";
public static ArrayList<String> list = new ArrayList<>();
// DFS走迷宫,记录所有可行路径
public static void dfsMap(int x, int y, int[][] map) {
// 矩阵大小, m 行 n 列
int m = map.length;
int n = map[0].length;
// 套路,上来先设置结束条件
if (x < 0 || y < 0 || x > m - 1 || y > n - 1 || map[x][y] == 1)// 如果坐标越界,或者 maze[x][y]==1 表示遇到障碍
return;
if (x == m - 1 && y == n - 1) { // 判断是否抵达出口
path = path + "(" + x + "," + y + ")";
list.add(path); // 将所有通路加入到list中
return;
}
String temp = path;
path = path + "(" + x + "," + y + ")" + "→"; // 记录路线
map[x][y] = 1; // 将走过的路标记为1
// 向四个方向搜索,方向可以任意排列
dfsMap(x, y + 1, map); // 向右搜索
dfsMap(x + 1, y, map); // 向下搜索
dfsMap(x, y - 1, map); // 向左搜索
dfsMap(x - 1, y, map); // 向上搜索
map[x][y] = 0;// 恢复标记
path = temp; // 回溯路径
}
public static void main(String[] args) {
// 初始化一个迷宫地图
// 0: 表示通路,1:表示死路
int[][] map = {
{ 0, 0, 0 },
{ 0, 1, 0 },
{ 0, 0, 0 }
};
int[][] map2 = {
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 1, 0, 1, 1, 1, 1, 1, 1, 1, 1 },
{ 1, 0, 1, 1, 0, 1, 1, 0, 1, 0 },
{ 1, 0, 1, 0, 0, 1, 0, 0, 1, 0 },
{ 1, 0, 1, 0, 1, 0, 1, 0, 1, 0 },
{ 0, 0, 1, 1, 1, 1, 1, 1, 1, 0 },
{ 1, 0, 1, 1, 1, 1, 1, 1, 1, 0 },
{ 1, 0, 1, 0, 0, 1, 0, 0, 1, 0 },
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 }
};
// DFS从(0,0)开始走
dfsMap(0, 0, map);
if (list.size() != 0) {
System.out.println("打印所有通路:");
for (String str : list) {
System.out.println("找到路径:" + str);
}
System.out.println("-----------------------");
System.out.println("打印按右、下、左、上方向的dfs找到的第一条最短路径:");
System.out.print("最短路线:");
long startTime = System.nanoTime();
String shortestPath = list.get(0);
for (int i = 0; i < list.size() - 1; i++) {
if (list.get(i).length() < shortestPath.length()) {
shortestPath = list.get(i);
}
}
System.out.println(shortestPath);
String[] shortestLength = shortestPath.split("→");
System.out.println("最短路径步数:"+(shortestLength.length-1));
long endTime = System.nanoTime();
double runTime = (endTime - startTime) / 1000000.000;
System.out.println("-----------------------");
System.out.println("运行用时:" + runTime + " ms");
System.out.println("-----------------------");
System.out.println("打印所有最短路径:");
ArrayList<String> shortestPathArray = new ArrayList<>();
String shortestPath2 = list.get(0);
for (int i = 0; i < list.size() - 1; i++) {
if (list.get(i).length() <= shortestPath2.length()) {
shortestPath2 = list.get(i);
}
}
for (String str : list) {
if (str.length() == shortestPath2.length()) {
shortestPathArray.add(str);
}
}
for (String shortest : shortestPathArray) {
System.out.println("最短路径之一:" + shortest);
}
} else {
System.out.println("没有找到路线!");
}
}
}
趁着对上面代码理解的余温,赶紧再看下面这道类似的题。
【第一道题】


对于这个问题,首先,题意很难读懂,题中说了个“上下左右”一下子就把人带坑里了,让人以为只有满足上下左右加中间,这样的才算是岛屿。其实不然,只要陆地四周环海,那它就是岛屿,那怕就一块陆地。
我觉得出题人说上下左右的意思是想强调一下,边缘的陆地会被淹没,如果一块陆地上下左右都是陆地,那么它就不会淹没
时间有点来不及了,我先贴上我参考的文章,大家可以进去看看:
【CSDN】Troc《蓝桥杯第九届之全球变暖》
【第二道题】

刚看到这道题的时候,仿佛做过一样,这道题和以前那些都不一样。前两篇文章一直是在一维的世界里混的,这篇文章上升到了二维世界。
按照我们dfs的套路,依然是上来先设数组,这里按照题意我们需要一个3行4列的二维数组来记录整个方格的所有数
public static int[][] map = new int[3][4];
因为仅仅是往里填数,不用比较或者求和之类的,所以这个二维数组不必作为参数,参数只需要x,y坐标即可
dfs()方法定义如下
public static void dfs(int x, int y)
深度优先搜索会从从左上角开始往二维数组里填数字,当到达右下角的时候就该递归结束了,所以递归结束条件代码如下
if(x == m-1 && y == n-1) { // 到达出口
count++;
return;
}
上面的代码都还可以理解,这道题难就难在如何进行搜索,这道题相当具有典型,望大家重视接下来的代码!
因为我们的数组是个3行4列,二维形状,所以我们可以一行一行的填,也可以一列一列的填,个人倾向按行填,符合阅读习惯。按行填的话,就是x坐标不变,y+1;当y越界的时候,换行,y重新从0开始。代码如下:
if(y >= n) { // y坐标越界
dfs(x + 1, 0); // 换行,y从0开始
} else {
for(int i=0; i<=9; i++) {
// 搜索来构建矩阵
if(visited[i] == 0 && checked(x,y,i)) { //checked()检查(x,y)坐标周围的数与我们要填的数i的关系是否满足不连续
visited[i] = 1;
map[x][y] = i;
dfs(x,y+1); // 一行一行填
map[x][y] = 100;
visited[i] = 0;
}
}
}
像上面的代码如果我没做过这道题,我是写不出来的。
上面还有个要说的就是checked()这个方法,题意要求连续的两个数不能相邻。所以我们需要检查(x,y)坐标周围的八个坐标的值与 i 的差的绝对值是否为1,如果为1,代表连续,不能填。
它们的坐标关系示意如下:
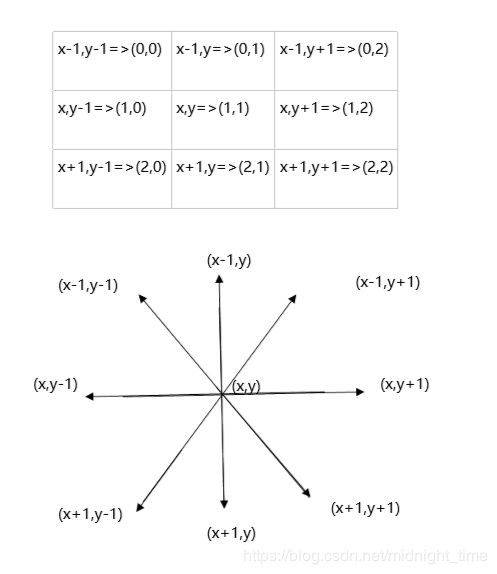
检查代码如下:
public static boolean checked(int x, int y, int num) {
if(x>=0 && y>=0 && x<m && y+1<n) {
if(Math.abs(map[x][y+1] - num) == 1) {
return false;
}
}
if(x>=0 && y<n && x<m && y-1>=0) {
if(Math.abs(map[x][y-1] - num) == 1) {
return false;
}
}
if(x>=0 && y>=0 && x+1<m && y<n) {
if(Math.abs(map[x+1][y] - num) == 1) {
return false;
}
}
if(x<m && y>=0 && x-1>=0 && y<n) {
if(Math.abs(map[x-1][y] - num) == 1) {
return false;
}
}
if(x>=0 && y>=0 && x+1<m && y+1<n) {
if(Math.abs(map[x+1][y+1] - num) == 1) {
return false;
}
}
if(x<m && y<n && x-1>=0 && y-1>=0) {
if(Math.abs(map[x-1][y-1] - num) == 1) {
return false;
}
}
if(x>=0 && y<n && x+1<m && y-1>=0) {
if(Math.abs(map[x+1][y-1] - num) == 1) {
return false;
}
}
if(x<m && y>=0 && x-1>=0 && y+1<n) {
if(Math.abs(map[x-1][y+1] - num) == 1) {
return false;
}
}
return true;
}
上面一大堆代码看着就让人头大,以我的水平,也只能写成这样了。不过,还是有人把它给简化了,代码如下:
public static int dir[][] = new int[][]{
{0, -1},
{-1, -1},
{-1, 0},
{-1, 1}
};
public static boolean checked(int x, int y, int num) {
for (int i = 0; i < 4; i++) {
int nx = x + dir[i][0];
int ny = y + dir[i][1];
if (nx >= 0 && nx < 3 && ny >= 0 && ny < 4) {
//相邻的点有相邻的数字
//还没有填过数字的格子-10 肯定不会等于当前格子0-9 +1或-1
if (map[nx][ny] == num - 1 || map[nx][ny] == num + 1) {
return false;
}
}
}
return true;
}
人家用一个二维数组来实现的,充分体现了一句话“数据结构学的好,代码写的少!”
最后再提醒一点,按行,一行一行递归的话,main()方法里面dfs起始坐标是(0,1)
如果你想按列,一列一列递归的话,需要修改一下搜索的条件,main()方法里面的起始坐标就是(1,0)
【完整代码】
public class 方格填数dfs {
public static int count;
public static int[][] map = new int[3][4];
public static int[] visited = new int[10];
// 矩阵大小
public static int m = map.length;
public static int n = map[0].length;
// 为了减少网页上代码行数,这里就用大佬写的代码了
// 如果看不懂,请自行替换为我那种八个坐标挨个判断的原始方法
public static int dir[][] = new int[][]{
{0, -1},
{-1, -1},
{-1, 0},
{-1, 1}
};
public static boolean checked(int x, int y, int num) {
for (int i = 0; i < 4; i++) {
int nx = x + dir[i][0];
int ny = y + dir[i][1];
if (nx >= 0 && nx < 3 && ny >= 0 && ny < 4) {
//相邻的点有相邻的数字
//还没有填过数字的格子-10 肯定不会等于当前格子0-9 +1或-1
if (map[nx][ny] == num - 1 || map[nx][ny] == num + 1) {
return false;
}
}
}
return true;
}
public static void dfs(int x, int y) {
if(x == m-1 && y == n-1) { // 到达出口
count++;
// 打印全部可能
/*
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
System.out.println();
*/
return;
}
if(y >= n) { // y坐标越界
dfs(x + 1, 0); // 换行,y从0开始
} else {
for(int i=0; i<=9; i++) {
// 搜索构建矩阵
if(visited[i] == 0 && checked(x,y,i)) { //checked()检查(x,y)坐标周围的数与我们要填的数i的关系是否满足不连续
visited[i] = 1;
map[x][y] = i;
dfs(x,y+1);
map[x][y] = 100;
visited[i] = 0;
}
}
}
}
public static void main(String[] args) {
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
map[i][j] = 100;
}
}
dfs(0,1);
System.out.println(count); // 答案:1580
}
}
【第三道题】

现在是晚上0:38,夜深了,我已经学不动了…,对于这道题,可以参考下面这篇文章
【CSDN】Daemoonn《2016蓝桥杯省赛C/C++B组7题剪邮票 DFS枚举组合情况BFS判联通》
上面有两道题没有分析,有时间的话我再回来补吧。其实有些问题我自己还没搞懂呢。这三篇文章大致就是这个样子了,希望大家看完之后,可以对dfs算法有个全面的了解。
我的上两篇文章 → 《【算法】蓝桥杯dfs深度优先搜索之排列组合总结》
→ 《【算法】蓝桥杯dfs深度优先搜索之凑算式总结》
【参考文章】
【CSDN】梅森上校《JAVA版本:DFS算法题解两个例子(走迷宫和求排列组合数)》
【CSDN】Daemoonn《2016蓝桥杯省赛C/C++B组7题剪邮票 DFS枚举组合情况BFS判联通》
【CSDN】Daemoonn《2016蓝桥杯C/C++省赛B组第6题 方格填数 DFS》
【CSDN】广海_小疯疯丶《2018年第九届蓝桥杯【C++省赛B组】【第九题:全球变暖】——广搜BFS解法,附解题代码》
【CSDN】Troc《蓝桥杯第九届(C/C++B组)题目汇总及解析》
【CSDN】Troc《蓝桥杯第九届之全球变暖》