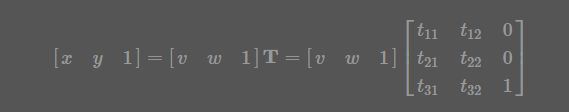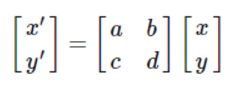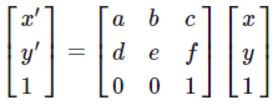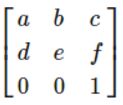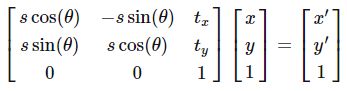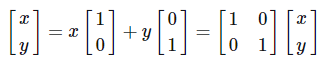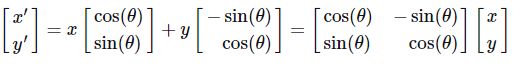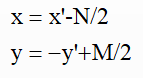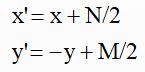CV笔记3：图像几何变换(基于python-opencv实现)

目录

一、简介

二、常见仿射变换

三、 算法理论介绍

3.1 变换形式

3.2 变换矩阵的理解和记忆

四、坐标系变换

4.1 图像坐标系与笛卡尔坐标系转换关系：

五、反向映射

六、 插值

代码实现

参考

---

一、简介

几何变换的原理大多都是相似，只是变换矩阵不同，因此，我们以最常用的平移和旋转为例进行学习。在深度学习领域，我们常用平移、旋转、镜像等操作进行数据增广；在传统CV领域，由于某些拍摄角度的问题，我们需要对图像进行矫正处理，而几何变换正是这个处理过程的基础，因此了解和学习几何变换也是有必要的。

这次我们带着几个问题进行，以旋转为例：

• 1：变换的形式（公式）是什么？
• 2：旋转中心是什么？毕竟以不同位置为旋转中心得到的结果是不一样的。
• 3：采用前向映射还是反向映射？(反向映射更为有效)
• 4：采用反向映射后，采用何种插值算法？最常用的的是双线性插值，OpenCV也是默认如此。

二、常见仿射变换

常见的变换可以总结为：

相似变换 (similarity transform) = 旋转 (rotation) + 平移 (translation) + 缩放 (scale)

仿射变换 (Affine Transform) = 平移 (Translation) + 缩放 (Scale) + 翻转 (Flip) + 旋转 (Rotation) + 斜切 (Shear)

投影变换 (perspective transform) = 旋转 + 平移 + 缩放 + 切变 + 射影

---

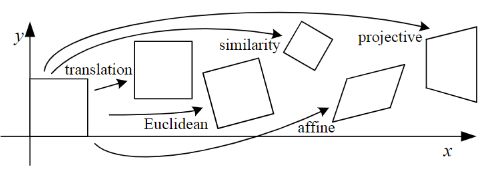
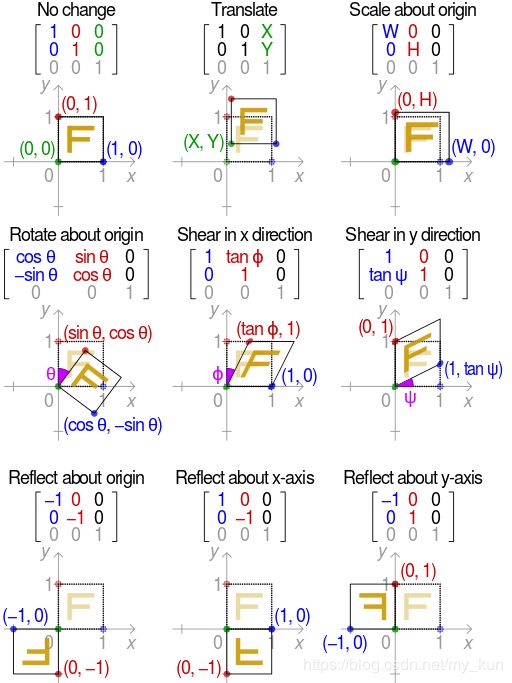
2D图像常见的坐标变换如下图所示：

这篇文章不包含透视变换（projective/perspective transformation），而将重点放在仿射变换（affine transformation），将介绍仿射变换所包含的各种变换，以及变换矩阵该如何理解记忆。

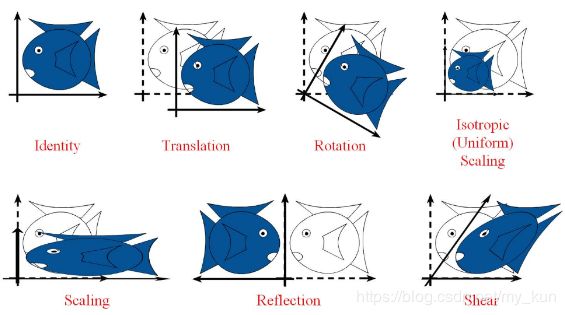
仿射变换：平移、旋转、放缩、剪切、反射

仿射变换包括如下所有变换，以及这些变换任意次序次数的组合：

平移（translation）和旋转（rotation）顾名思义，两者的组合称之为欧式变换（Euclidean transformation）或刚体变换（rigid transformation）；

放缩（scaling）可进一步分为uniform scaling和non-uniform scaling，前者每个坐标轴放缩系数相同（各向同性），后者不同；如果放缩系数为负，则会叠加上反射（reflection）——reflection可以看成是特殊的scaling；

刚体变换+uniform scaling 称之为，相似变换（similarity transformation），即平移+旋转+各向同性的放缩；

剪切变换（shear mapping）将所有点沿某一指定方向成比例地平移，语言描述不如上面图示直观。

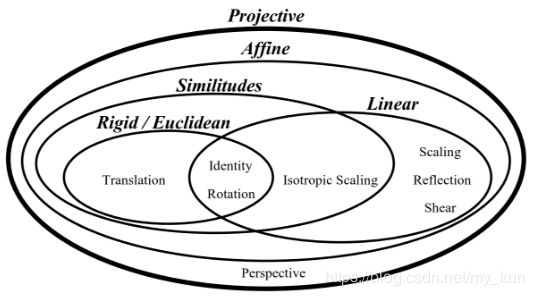
各种变换间的关系如下面的venn图所示：

通过变换矩阵可以更清晰地看出这些变换间的关系和区别。

三、 算法理论介绍

3.1 变换形式

先看第一个问题，变换的形式。我们先给出基本的结论。与OpencV不同的是这里采取冈萨雷斯的《数字图像处理_第三版》的变换矩阵方式，关于OpenCV的策略可以看它的官方文档。根据冈萨雷斯书中的描述，仿射变换的一般形式如下：

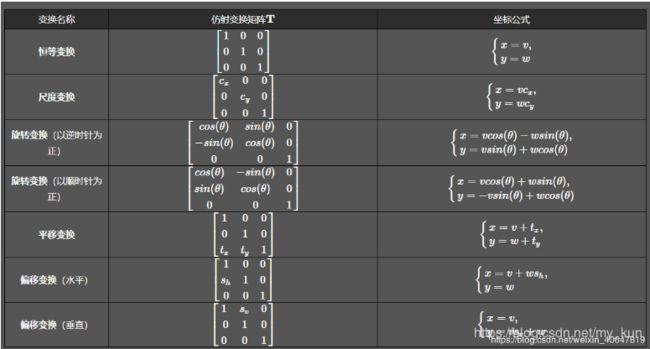
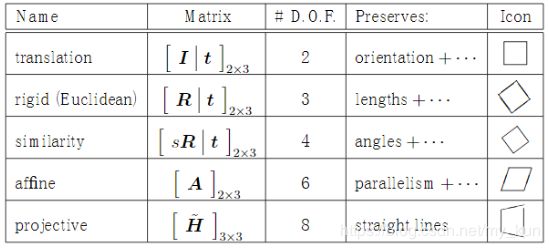
式中的T就是变换矩阵，其中 (v,w)为原坐标，(x,y) 为变换后的坐标，不同的变换对应不同的矩阵，这里也贴出来吧，一些常见的变换矩阵及作用如下表：

也就是说，我们根据自己的目的选择不同变换矩阵就可以了。

我们详细的讲解一下变换矩阵的由来。图像变换时，变换矩阵的目标是通过该矩阵找到原来坐标变换后的坐标位置，因此我们的操作对象是像素的坐标。

注：在本节中，下面讲解将变换矩阵放在了原坐标的左边进行左乘，而在上面的结论中和其他小节中采用的是右乘的方式。

没有平移或者平移量为0的所有仿射变换可以用如下变换矩阵描述（其中x和y为原坐标）：

不同变换对应的a,b,c,d约束不同，排除了平移变换的所有仿射变换为线性变换（linear transformation），其涵盖的变换如上面的venn图所示，其特点是原点位置不变，多次线性变换的结果仍是线性变换。

为了涵盖平移，引入齐次坐标，在原有2维坐标的基础上，增广1个维度，如下所示：

所以，仿射变换的变换矩阵统一用下面的矩阵M来描述，

不同基础变换的a,b,c,d,e,f约束不同，如下所示：

 

此外，旋转和平移相乘得到刚体变换的变换矩阵，如下，有3个自由度（θ,tx,ty），这里旋转方向为逆时针方向，因此与上图中的正负号不同，

再乘上uniform scaling得到相似变换，有4个自由度（s,θ,tx,ty），如下：

 

自然，仿射变换的变换矩阵有6个自由度（a,b,c,d,e,f）。

3.2 变换矩阵的理解和记忆

坐标系由坐标原点和基向量决定，坐标原点和基向量确定了，坐标系也就确定了。

对于坐标系中的位置(x,y)，其相对坐标原点在[1,0]方向上的投影为x，在[0,1]方向上的投影为y——这里投影的意思是过(x,y)做坐标轴的平行线与坐标轴的交点到原点的距离，即(x,y)实际为：

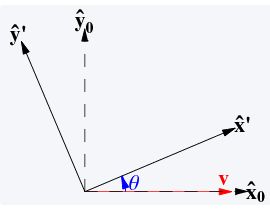
当坐标系变化，坐标系中的点也跟着变化，但点相对新坐标系（x′−y′坐标系）的位置不变仍为(x,y)，以旋转变换为例，新坐标轴的基向量则变为[cos(θ),sin(θ)]和[−sin(θ),cos(θ)]，所以点变化到新位置为：

新位置和新基向量是相对绝对坐标系(x−y坐标系）而言的。其他变换矩阵同理。

总结一下：

• 所有变换矩阵只需关注一点：坐标系的变化，即基向量和原点的变化；
• 坐标系变化到哪里，坐标系中的所有点也跟着做同样的变化；

这时再对照上面的各种变换矩阵，就很好理解了。

四、坐标系变换

再看第二个问题，变换中心，对于缩放、平移可以以图像坐标原点（图像左上角为原点）为中心变换，这不用坐标系变换，直接按照一般形式计算即可。而对于旋转和偏移，一般是以图像中心为原点，那么这就涉及坐标系转换了。

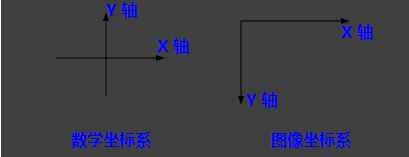
我们都知道，图像坐标的原点在图像左上角，水平向右为 X 轴，垂直向下为 Y 轴。数学课本中常见的坐标系是以图像中心为原点，水平向右为 X 轴，垂直向上为 Y 轴，称为笛卡尔坐标系。看下图:

因此，对于旋转和偏移，就需要3步（3次变换）：

• 将输入原图图像坐标转换为笛卡尔坐标系；
• 进行旋转计算。旋转矩阵前面已经给出了；
• 将旋转后的图像的笛卡尔坐标转回图像坐标。

4.1 图像坐标系与笛卡尔坐标系转换关系：

先看下图：

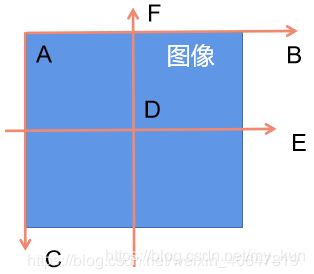
在图像中我们的坐标系通常是AB和AC方向的,原点为A，而笛卡尔直角坐标系是DE和DF方向的，原点为D。 令图像表示为M×N的矩阵，对于点A而言，两坐标系中的坐标分别是(0，0)和(-N/2,M/2)，则图像某像素点(x',y')转换为笛卡尔坐标（x,y）转换关系为，x为列，y为行：

逆变换为：

于是，根据前面说的3个步骤（3次变换），旋转(顺时针旋转)的变换形式就为，3次变换就有3个矩阵：

五、反向映射

看第3个问题，在冈萨雷斯的《数字图像处理_第三版》中说的很清楚，前向映射就是根据原图用变换公式直接算出输出图像相应像素的空间位置，那么这会导致一个问题：可能会有多个像素坐标映射到输出图像的同一位置，也可能输出图像的某些位置完全没有相应的输入图像像素与它匹配，也就是没有被映射到，造成有规律的空洞（黑色的蜂窝状）。更好的一种方式是采用 反向映射（Inverse Mapping）：扫描输出图像的位置(x,y)，通过

（为T的逆矩阵）计算输入图像对应的位置 (v,w)，通过插值方法决定输出图像该位置的灰度值。

六、 插值

第4个问题，采用反向映射后，需通过插值方法决定输出图像该位置的值，因此需要选择插值算法。通常有最近邻插值、双线性插值，双三次插值等，OpencV默认采用双线性插值，我们也就采用双线性插值。

图像插值算法介绍：CV笔记2：图像插值算法—最近邻插值、双线性插值

 

代码实现

Opencv-Python学习笔记五——图像翻转，平移，仿射及透视 warpAffine

参考

仿射变换及其变换矩阵的理解