NavMesh生成研究（三）：轮廓生成

本文翻译自：http://critterai.org/projects/nmgen_study/contourgen.html

注：因第二步——区域生成的基本内容被我写的原创文章涵盖，因此不再花时间单独翻译，想了解这一步的可参见文章。

概述

这篇文章描述了构造导航网格过程中的第三步：简单多边形（轮廓和凹面）的生成，它们代表着源几何体的可行走表面区域。这些轮廓仍然由体素空间(voxel space)的单位来表示，但是这是从体素空间转向向量空间(vector space)的第一步。

源数据类：OpenHeightfield
构造类：ContourSetBuilder
数据类：ContourSet 和 Contour

如果你需要回忆这一步的大致过程，请回到总体概述。

寻找区域边界

从开放高度域结构迁移到轮廓结构时，最大的概念上的改变是从关注区间(span)的表面改为关注区间的边界(edge)。

对于轮廓来说，我们关心的是区间的边界。有两种类型的边界：区域(region)和内部(internal)。同样作为区间边界，区域边界隔开了不同区域，而内部边界隔开的是同一区域。

下面几个例子为了看得方便，简化成了2D模型。我们稍后会回到3D模型。

在这一步中我们想要将边界分成区域边界和内部边界两类。这个信息很容易得到：我们遍历所有的区间，对于每个区间我们检查它所有的邻接区间(axis-neighbours)，如果这个领接区间与它不在同一区域类，那么把边界标记为区域边界。

寻找区域轮廓

一旦我们知道哪个区间边界是区域边界后，我们就能够沿着边界构建轮廓了。我们再一次遍历所有区间，若它拥有一条区域边界，则：

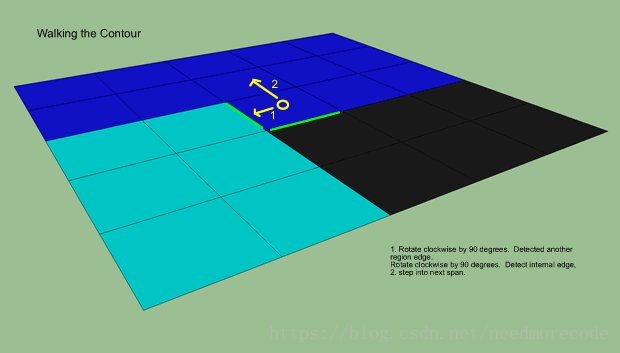
从面向已知的区域边界开始。将它添加到轮廓中。

旋转90度，继续添加区域边界到轮廓中，直到我们找到一条内部边界。前进一步到邻接区间中。

再逆时针方向旋转90度，重复执行前面的步骤。反复执行，直到我们回到初始的区间，面对初始的方向。

从边界到顶点

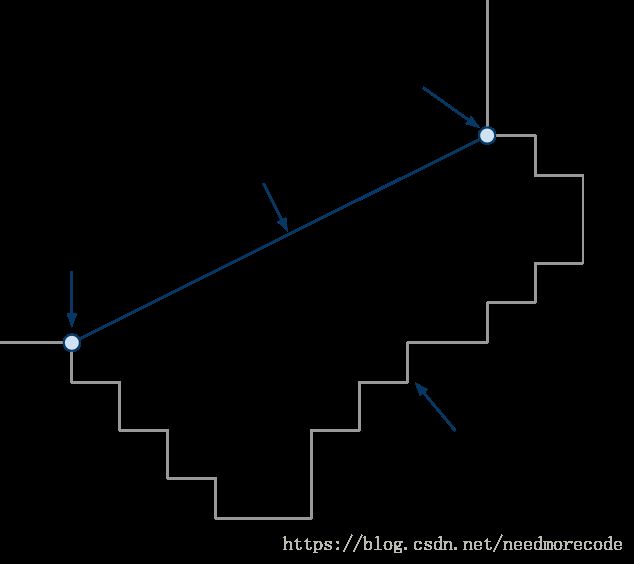
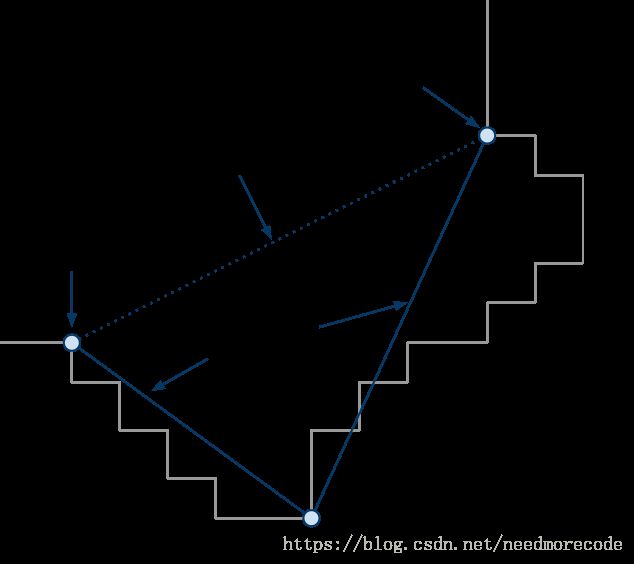
如果我们想回到向量空间的话，我们需要的是顶点，而非边界。顶点的(x, z)值很容易确定。对于每条边界，我们取它的顺时针方向的区间的顶角的(x, z)值（从区间内部看）。

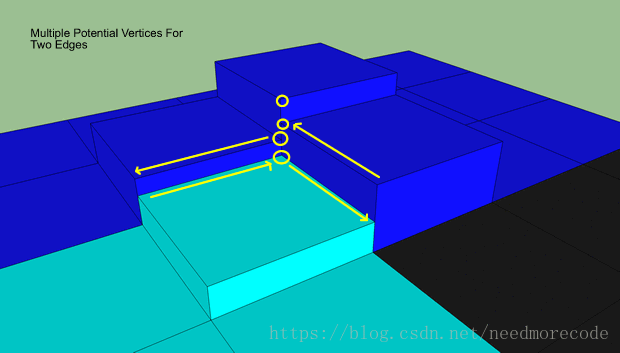
求顶点y值的过程有一些技巧。在这里我们回到3D模型中。在下面的例子中，应该选取哪个顶点呢？

所有的边界顶点有最多4个可能的y值。应选取最高的y值，理由有二：它保证了最终的顶点(x, y, z)在源网格表面之上。再者，它提供了一种通用的选择机制来确保使用这个顶点的所有轮廓将使用同样的高度。

简化轮廓

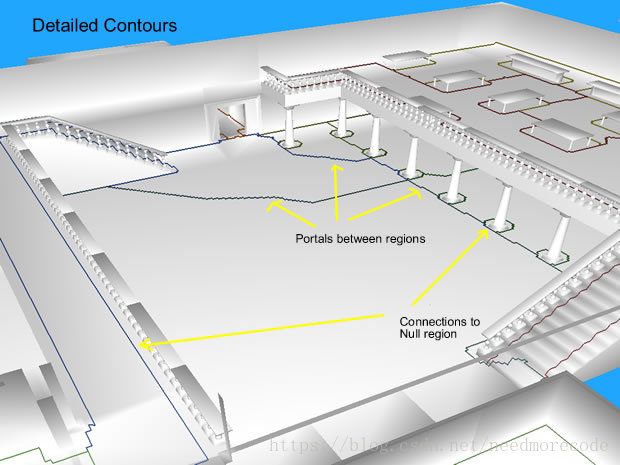
到这一步，我们为所有的区域生成了轮廓。轮廓是由从区间角继承来的顶点构造。下面是一个宏观的视角。

注意有两种类型的轮廓部分。一种是两个相邻区域的入口，另一种则是与“空地”(empty space)相邻。在代码文档中，“空地”被称作“无效区域”(null region)。我也将在这里使用同样的术语。

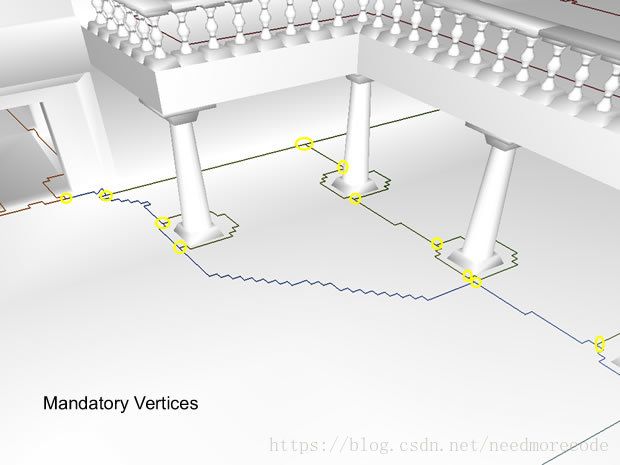
那么真的需要这么多顶点吗？即使在直线轮廓上，每个区间都有构造边界的顶点。显然答案是不需要。唯一必需的顶点是在发生区域连接改变的地方，例如：区域入口的边界上。

简化区域-区域入口是件容易的事情。我们先将所有顶点丢弃，只保留必需的(mandatory)顶点。

对于到无效区域的连接要稍微复杂一些。这里使用了两个算法。

第一个是由MatchNullRegionEdges实现的Douglas-Peucker算法。它使用edgeMaxDeviation参数来决定将哪些顶点丢弃以获得简化的线段。它起始于必需的顶点，然后将顶点加回，并确保没有一个起始点与简化边界之间的距离大于edgeMaxDeviation。

一步步讲解：开始时是最简单的可能边界。

从简化边界找到最远的点。若它超过了edgeMaxDeviation，则将其加回到轮廓中。

重复这个过程，直到再也没有一个顶点与简化边界的距离超过允许值。

简化轮廓的一个简单例子：

正如之前提到的，另一个算法用于连接到无效区域的边界。第一个算法能够产生长线段，它们会在后面的网格生成过程中用于计算长且薄的三角形。第二个算法由NullRegionMaxEdge实现，它使用maxEdgeLength参数来重新插入顶点，并确保没有一条线段超过最大长度。实现方法是检测到长的边界，将其切成两半。重复这个过程直到再也没有超长的边界。

作为一个对最终网格影响的例子，在处理前：

在处理后：

目前的进展

在这一步的结尾，我们得到了形状是简单多边形的轮廓。顶点仍然处于体素空间中，但我们已经在返回向量空间的道路上顺利前行。