【数据结构】限定性线性表——栈与队列 总结

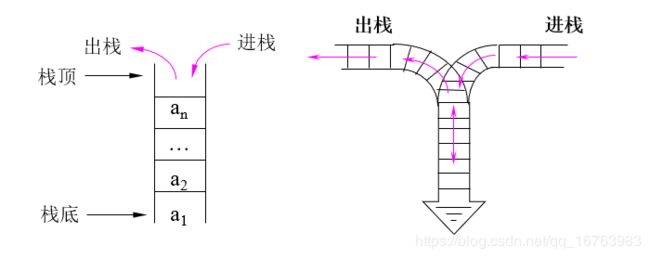
一、顺序栈 LIFO

（一）栈的声明

#define Stack_Size 100
typedef struct{
    StackElementType elem[Stack_Size];
    int top;
}SeqStack;

（二）栈的操作

1、初始化栈——构造空栈 top == -1

void InitStack(SeqStack* S){
    S->top=-1;
}

2、判栈空

int IsEmpty(SeqStack* S){
    return (S->top == -1);
}

3、判栈满

int IsFull(SeqStack* S){
    return (S->top == Stack_Size-1);
}

4、出栈

int Pop(SeqStack* S, StackElementType* x){
    if(IsEmpty) return (FALSE);
    else{
        *x=S->elem[S->top];
        S->top--;
        return (TRUE);
    }
}

5、取栈顶元素

在出栈的基础上，不弹出即可

int GetTop(SeqStack* S, StackElementType* x){
    if(IsEmpty) return (FALSE);
    else{
        *x=S->elem[S->top];
    }
}

二、链栈 LIFO

（一）栈的声明

typedef struct node{
    StackElementType data;
    struct node *next;
}LinkStackNode;
typedef LinkStackNode *LinkStack;

（二）栈的操作

1、进栈

如下代码中的top即是栈顶指针

int Push(LinkStack top, StackElementType x){
    LinkStackNode* temp;
    temp=(LinkStackNode*)malloc(sizeof(LinkStackNode));
    if(temp==NULL) return (FALSE); //申请内存空间失败
    temp->data=x;
    //头插法
    temp->next=top->next;
    top->next=temp;
    return (TRUE);
}

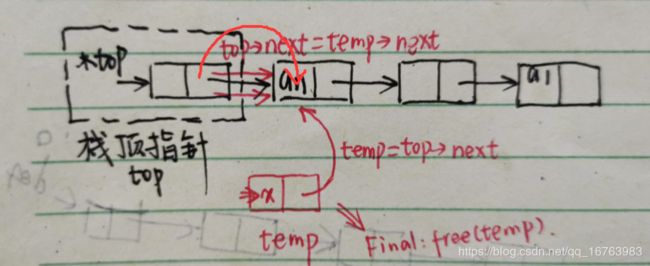
2、出栈

int Pop(LinkStack top, StackElementType *x){
    LinkStackNode* temp=top->next;
    if(temp==NULL) return (FALSE);
    top->next=temp->next;
    *x=temp->data;
    free(temp);
    return (TRUE);
}

（三）栈的应用

1、十进制转二进制

void Conversion10_2(int N){
    Stack S;
    int x;
    while(N>0){
        x=N%2;
        Push(&S,x);
        N/=2;
    }
    while(!IsEmpty(S)){
        Pop(&S,&x);
        cout<<x;
    }
}

2、括号匹配问题

思路：遍历整个字符串，如果遇到左括号则入栈，遇到右括号则检查栈是否空，如空则右括号多余 return，非空则取栈顶，如与右括匹配，则继续遍历字符串，如不匹配则失败return！遍历完整个字符串后，再去检查一次栈，如果空了，说明匹配成功，如果非空，则左括号多余，失败于黎明之前。

void BracketMatch(char *str){
    Stack S;
    int i;
    char ch;
    InitStack(&S);
    //扫描字符串
    for(i=0;str[i]!='\0';i++){
        switch(str[i]){
            case '(': case'[': case'{': //左括号入栈
                Push(&S,str[i]);
            case ')': case']': case'}':
                if(IsEmpty(S)){
                    cout<<"右括号多余！";
                    return ;
                }else{
                    GetTop(&S,&ch);
                    if(Match(ch,str[i])) Pop(&S,&ch);
                    else{
                        cout<<"左右括号不匹配！";
                        return ;
                    }
                }
        }
    }
    //扫描完后检查栈是否还有括号
    if(!IsEmpty(S)) cout<<"左括号多余！";
    else cout<<"左右括号完全匹配";
}

三、队列 FIFO

（一）链队列的声明

typedef struct Node{
    QueueElementType data;
    struct Node *next;
}LinkQueueNode;
//连续声明
typedef struct{
    LinkQueueNode *front;
    LinkQueueNode *rear;
}LinkQueue;

（二）队列的操作

1、队列初始化

int InitQueue(LinkQueue *Q){
    Q->front=(LinkQueueNode*)malloc(sizeof(LinkQueueNode));
    if(Q->front!=NULL){
        Q->rear=Q->front; //初始化队列为空链，头指针即尾指针
        Q->front->next=NULL;
        return (TRUE);
    }else{
        return (FALSE);
    }
}

2、入队

插入在尾部——尾插法

int EnterQueue(LinkQueue* Q, QueueElementType x){
    LinkQueueNode* new_node;
    new_node=(LinkQueueNode*)malloc(sizeof(LinkQueueNode));
    if(new_node==NULL) return (FALSE);
    new_node->data=x;
    //尾插法在尾部
    new_node->next=NULL; //插入在尾部
    Q->rear->next=new_node;
    Q->rear=new_node;
    return (TRUE);
}

3、出队

其实就是先定位队头再用队头结点绕过的操作

int DeleteQueue(LinkQueueNode* Q, QueueElementType* x){
    LinkQueueNode* p;
    if(Q->front==Q->rear) return (FALSE); //空队
    p=Q->font->next; //队头
    Q->front->next=p->next; //绕过队头
    if(Q->rear==p) Q->rear=Q->front; //队中只有一个元素，重置
    *x=p->data;
    free(p);
    return (TRUE);
}

四、循环队列

用连续存储单元存放元素，类似于顺序栈，设队列数组是Queue[MAXSIZE]，最后一个单元是Queue[MAXSIZE-1]，后继是Queue[0]，则

• rear+1==MAXSIZE时，rear=0
• rear=(rear+1) mod MAXSIZE

（一）循环队列的声明

const int MAXSIZE = 100;
typedef struct{
    QueueElementType element[MAXSIZE];
    int front;
    int rear;
}SeqQueue;

（二）循环队列的操作

1、初始化队列

void InitQueue(SeqQueue* Q){
    Q->front=Q->rear=0;
}

2、入队

int EnterQueue(SeqQueue* Q, QueueElementType x){
    if((Q->rear+1)%MAXSIZE==Q->front) return (FALSE); //队满
    Q->element[Q->rear]=x;
    Q->rear=(Q->rear+1)%MAXSIZE;
    return (TRUE);
}

3、出队

int DeleteQueue(SeqQueue* Q, QueueElementType* x){
    if(Q->front==Q->rear) return (FALSE); //队空
    *x=Q->element[Q->front];
    Q->front=(Q->front+1)%MAXSIZE;
    return (TRUE);
}

本文更新至2020.7.5

---