教程 | TensorFlow 2.0 教程 —— 机器学习基础 —— 回归(2)
译自:TensorFlow 官方教程
由于 TensorFlow 2.0 的回归教程使用了另一个数据集,因此保留之前版本中使用的波士顿住房数据集。
传送门
预测燃油效率:回归
- Auto MPG 数据集
- 获取数据
- 清洗数据
- 将数据划分为训练集和测试集
- 检查数据
- 从标签中分离特征
- 归一化数据
- 模型
- 建立模型
- 检查模型
- 训练模型
- 做出预测
- 结论
在回归问题中,我们希望的预测输出是连续值,例如价格或者概率。
这个教程使用经典的 Auto MPG 数据集(MPG,每加仑汽油可行驶英里数)并且建立模型来预测十九世纪七十年代末及八十年代初的汽车燃油效率。我们提供了那个时间段的汽车的描述,包括汽缸、排量、马力和重量等属性。
from __future__ import absolute_import, division, print_function, unicode_literals
import pathlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
Auto MPG 数据集
获取数据
首先下载数据集。
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
Downloading data from http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data
32768/30286 [================================] - 0s 0us/step
'/root/.keras/datasets/auto-mpg.data'
使用 pandas 导入数据集。
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
清洗数据
数据集包含了一些未知的值。
dataset.isna().sum()
MPG 0
Cylinders 0
Displacement 0
Horsepower 6
Weight 0
Acceleration 0
Model Year 0
Origin 0
dtype: int64
为使教程简洁,直接丢弃包含这些值的行。
dataset = dataset.dropna()
“Origin” 列实际上是类别,而不是数值。因此将其转换为 one-hot 形式。
origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()
将数据划分为训练集和测试集
我们将使用测试集评估我们的最终模型。
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
检查数据
快速查看一下训练集中几对列的联合分布。
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
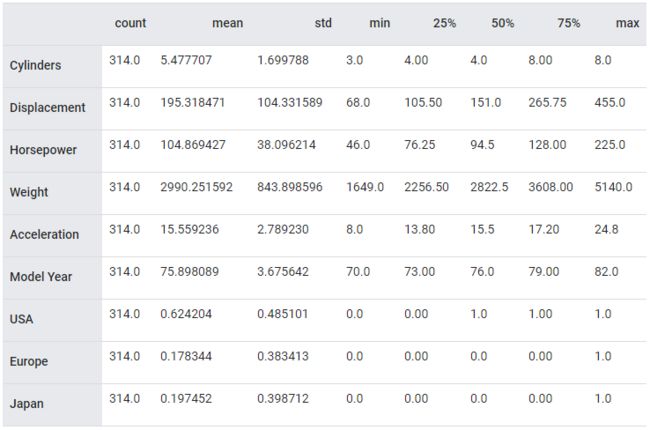
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
从标签中分离特征
标签是我们将要训练模型预测的值。
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
归一化数据
从上面的统计数据中可以看出,每个特征都在不同的范围。
将不同尺度和范围的特征归一化在大多数情况下都是重要的一步。虽然模型在不进行特征归一化的情况下可能会收敛,但这会增加训练的难度,并使生成的模型依赖于输入中使用的单元的选择。
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
注意: 这里用来归一化输入的统计值(均值和标准差)需要应用于任意送入模型的数据,并且要包含上面编码的 one-hot 变量。
模型
建立模型
我们将使用 Sequential 建立由两个密集连接隐藏层组成的模型,输出层返回一个单个且连续的值。建立模型的步骤包装在 build_model 函数里,因为我们后面会创建另一个模型。
def build_model():
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
return model
model = build_model()
检查模型
使用 .summary 方法可以打印模型的描述信息。
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 64) 640
_________________________________________________________________
dense_1 (Dense) (None, 64) 4160
_________________________________________________________________
dense_2 (Dense) (None, 1) 65
=================================================================
Total params: 4,865
Trainable params: 4,865
Non-trainable params: 0
_________________________________________________________________
现在试试这个模型。从训练集中选出 10 个样本,并且调用 model.predict。
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
array([[ 0.3297699 ],
[ 0.25655937],
[-0.12460149],
[ 0.32495883],
[ 0.50459725],
[ 0.10887371],
[ 0.57305855],
[ 0.57637435],
[ 0.12094647],
[ 0.6864784 ]], dtype=float32)
训练模型
训练模型 1000 个周期,并在 history 对象中记录训练和验证准确率。
# 在每个周期完成时打印一个点来显示训练进度
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
使用保存在 history 对象中的统计数据可视化模型的训练进度。
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mae'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mae'],
label = 'Val Error')
plt.ylim([0,5])
plt.legend()
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mse'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mse'],
label = 'Val Error')
plt.ylim([0,20])
plt.legend()
plt.show()
plot_history(history)
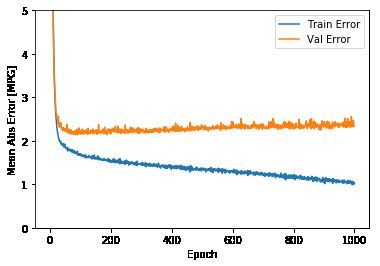
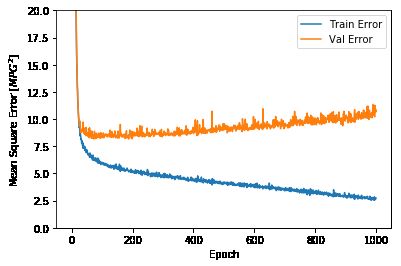
这张图显示,在大约 100 个周期之后,验证误差几乎没有改善,甚至有所上升。让我们更新 model.fit 使得模型在验证分数没有改善时自动停止训练。我们将使用 EarlyStopping 回调,如果一段周期中没有显示出性能改善,则自动停止训练。
这里有更多关于 回调 的信息。
model = build_model()
# patience 参数是检查性能改善的周期数
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
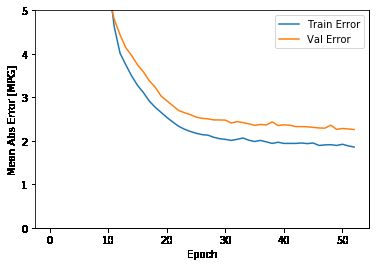
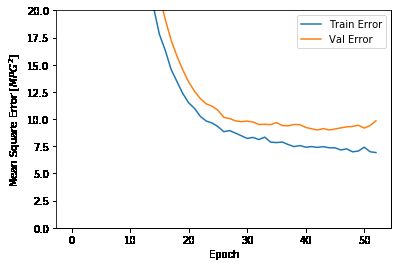
从图中可以看出,在验证集上,平均误差通常在 +/- 2 MPG 左右。
让我们使用测试集来看看模型的泛化能力如何。
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
Testing set Mean Abs Error: 2.09 MPG
做出预测
最后,使用测试集中的数据预测 MPG 值。
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
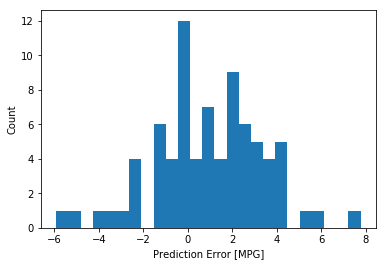
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
结论
本教程介绍了一些处理回归问题的技巧:
- 均方误差(MSE)是回归问题中常用的损失函数(不同于分类问题中的损失函数)
- 类似地,评估指标也不同于分类问题。常用的回归指标是平均绝对误差(MAE)。
- 当数值输入数据特征值有不同的范围时,应单独缩放每个特征到相同范围。
- 如果训练数据不多,一个技巧就是使用更少隐藏层的小网络来避免过拟合。
- 提前终止是预防过拟合的一个很有效的技巧。