Cplex求解器

博主个人博客

在求解整数线性规划问题是，Matlab下yalmip+cplex的组合会让如虎添翼。本人是在研究早晚班排班过程中才发现的这一工具。其能够求解各种整数规划模型。在matlab中使用cplex求解时，还可以使用yalmip工具进行建模，比直接使用cplex建模方便很多。

在正式开始使用前需要先安装好环境。第一步是下载相关的工具包。百度网盘链接 提取码：garx

yalmip安装

yalmip工具箱的安装比较简单，从链接下载后，将YALMIP-master文件夹拷贝到matlab>toolbox,如下图

是放在matlab安装目录的\toolbox文件夹下。

然后打开matlab，点击设置路径

点击添加并包含子文件夹，添加之后点击保存、关闭

这样下来，路径就设置好了，yalmip作为工具箱已经被添加到matlab中去了，接下来在命令行窗口输入中检查一下，输出yalmiptest,然后回车！你会发现你的yalmip已经可以作为matlab的工具箱而使用了，但是cplex没有被yalmip识别到，如下图所示，所以需要求解器cplex的安装

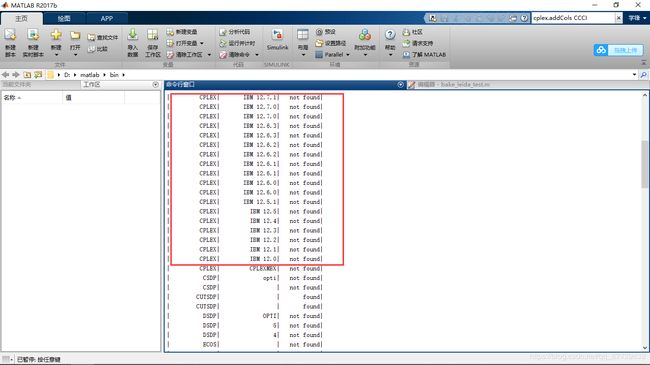
Cplex安装

Cplex的安装较yalmip复杂一些，不过复杂之处主要在版本对不对，能不能正常安装，是不是能够和yalmip匹配的上，以及最后求解的时候受不受到变量、约束个数的限制。

Cplex官网可以申请试用版，如果是在校学生或者老师，可以使用学校的教育邮箱去申请，理论上应该可以申请到。博主使用学校邮箱账号申请，奈何学校邮箱的问题迟迟收不到验证邮件消息，到第二天才收到了消息，所以并没有采用此种方法。而实直接在网上找了一个下载。原本想直接用一个简化版的Cplex的文件，但是添加到matlab路径后发现运行代码时找不到，照着网上的一些文章说是版本的问题，yalmip没有把对应的cplex版本包含进来，但是我查看了一下其实yalmip已经包含了很多版本的cplex。无奈之下我只好去下载CplexStudio.
按照博主链接，便可以下载到12.8版本的Cplex，解压后运行，一直点击下一步，改变安装路径和生成文件的路径，期间需要安装VS studio的环境，由于电脑早已有VS环境，可以忽略一些内容安装，总之，一般情况下，点击安装程序，一路点击下一步即可安装成功！

安装成功后，需要再次打开matlab，继续设置添加路径，这里需要注意的是，你需要将cpclex文件下matlab的文件夹添加进去。
接着进行测试，在命令行窗口输入yalmiptest，检查Cplex的安装情况，你会发现，yalmip检测到了求解器Cplex

到这里安装部分就都成功了，可以开始漫长的科研道路了。

一些示例

yalmip基本格式

1.创建决策变量
2.目标函数Z
3.约束条件设置C
4.参数设置

ops = sdpsetting('solver','Cplex','verbose',0); verbose:显示冗余度 0为只显示结果

5.求解

result = solvesdp(C,z,ops)

示例一

一个可视化公式编辑器的神器，它可以让我们可视化地编辑公式，然后自动得到它的LaTeX文本：

$$\begin{gathered} minZ=12x_1+5x_2+8x_3 \\ s.t.\{\begin{array}{l}2x_1+3x_2+x_3\ge 30\\ 4x_1+x_2+x_3\ge 15\\ x_1,x_2,x_3\ge 0\end{array} \end{gathered}$$

clear;clc;close all;

c = [12 5 8];
A = [2 3 1; 4 1 5];
b = [30; 15];

%决策变量
x = sdpvar(3,1);

%目标函数
z = c*x;

%添加约束
%C = [];
%C = [C; A*x >= b];
%C = [C;x>=0];
C=[A*x >= b,x>=0];
ops=sdpsettings('verbose',0);
%求解
result = optimize(C,z,ops);
if result.problem == 0    %求解成功
    x_star=double(x)
    z_star=double(z)
    else
    disp('求解过程中出错');
end

警告: 文件: C:\Program Files\IBM\ILOG\CPLEX_Studio_Community128\cplex\matlab\x64_win64\@Cplex\Cplex.p 行: 965 列: 0
在嵌套函数中定义 "changedParam" 会将其与父函数共享。在以后的版本中，要在父函数和嵌套函数之间共享 "changedParam"，请在父函数中显式定义它。
> In cplexoptimset
  In sdpsettings>setup_cplex_options (line 617)
  In sdpsettings (line 145)

x_star =

         0
    9.6429
    1.0714

z_star =

   56.7857

示例二 运输问题

$$\begin{gathered} minZ=\sum _{i=1}^m\sum _{j=1}^n{c}_{ij}{x}_{ij} \\ s.t.\{\begin{array}{l}{\sum }_{j=1}^n{x}_{ij}\le a_{i}i=1,2,\cdots ,m\\ {\sum }_{i=1}^m{x}_{ij}\ge b_{j}j=1,2,\cdots ,n\\ x_{ij}\ge 0i=1,2,\cdots ,m;j=1,2,\cdots ,n\end{array} \end{gathered}$$

clear;clc;close all;

c = [1 3 5 7 13; 6 4 3 14 8; 13 3 1 7 4;
    1 10 12 7 11];
a = [40 50 30 80];
b = [10 20 15 18 25];

%决策变量
x = intvar(4,5);

%目标函数
z = sum(sum(c.*x));

%添加约束
C = [];
for i=1:4
    C = [C; sum(x(i,:))<=a(i)];
end
for j=1:5
    C = [C;sum(x(:,j))>=b(j)];
end

C = [C;x>=0];
ops=sdpsettings('verbose',0);

result = optimize(C,z,ops);
if result.problem == 0    %求解成功
    x_star = double(x)
    z_star = double(z)
    else
    disp('求解过程中出错');
end

x_star =

     2    20     0    18     0
     0     0    10     0     0
     0     0     5     0    25
     8     0     0     0     0

z_star =

   331

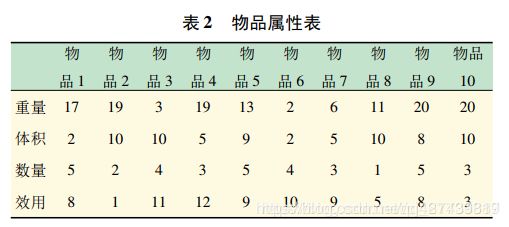
示例三 背包问题

$$\begin{gathered} minZ=\sum _{i=1}^n{c}_i{x}_i \\ s.t.\{\begin{array}{l}{\sum }_{i=1}^n{x}_i{w}_i\le W\\ {\sum }_{i=1}^n{x}_i{v}_i\le V\\ 0\le x_i\le n_i且为整数\end{array} \end{gathered}$$

clear;clc;close all;

c = [8 1 11 12 9 10 9 5 8 3]; %效用
w = [17 19 3 19 13 2 6 11 20 20]; %重量
v = [2 10 10 5 9 2 5 10 8 10];  %体积
n = [5 2 4 3 5 4 3 1 5 3];   %数量

%决策变量
x = intvar(10,1);

%目标函数
z = -(c*x);

%添加约束
C = [];
C = [C,w*x<=80];
C = [C,v*x<=60];
C = [C,0<=x<=n];

ops=sdpsettings('verbose',0);
%求解
result = optimize(C,z,ops);
if result.problem == 0    %求解成功
    x_star = double(x)
    z_star = double(-z)
    else
    disp('求解过程中出错');
end

x_star =

     1
     0
     3
     1
     0
     4
     3
     0
     0
     0

z_star =

   120

示例四 最短路径问题

% 利用yamlip求解最短路问题
clear;clc;close all;
D = load('1.txt');
n = size(D,1);

% 决策变量
x = binvar(n,n,'full');

% 目标
z=sum(sum(D.*x));
% 约束添加
C=[];
C = [C,(sum(x(1,:))-sum(x(:,1))==1)];
C = [C,(sum(x(n,:))-sum(x(:,n))==-1)];

for i=2:(n-1)
    C = [C,(sum(x(i,:))-sum(x(:,i))==0)];
end

ops=sdpsettings('verbose',0);
% 求解
result=solvesdp(C,z,ops);
if result.problem == 0
    x_star = value(x)
    z_star = value(z)
else
    disp('求解过程中出错');
end

x_star =

   NaN     1     0     0     0     0     0
     0   NaN     0     0     1     0     0
     0     0   NaN     0     0     0     0
     0     0     0   NaN     0     0     0
     0     0     0     0   NaN     0     1
     0     0     0     0     0   NaN     0
     0     0     0     0     0     0   NaN

z_star =

     5

示例五 指派问题

$$\begin{gathered} minZ=\sum _{i=1}^m\sum _{j=1}^n{c}_{ij}{x}_{ij} \\ s.t.\{\begin{array}{l}{\sum }_{i=1}^n{x}_{ij}=1i=1,2,\cdots ,n\\ {\sum }_{j=1}^n{x}_{ij}=1i=1,2,\cdots ,n\\ x_{ij}\left\{0,1\right\}i=1,2,\cdots ,n\end{array} \end{gathered}$$

clear;clc;close all;
c =load('zhipai.txt')


%决策变量
x = binvar(5,5,'full');

%目标函数
z = sum(sum(c.*x));

%添加约束
C = [];

C = [C;sum(x,1)==1];   %  1 横向相加
C = [C;sum(x,2)==1];   %  2 纵向相加

ops=sdpsettings('verbose',0);
%求解
result = optimize(C,z,ops);
if result.problem == 0    %求解成功
    x_star = double(x)
    z_star = double(z)
    else
    disp('求解过程中出错');
end

c =

    12     7     9     7     9
     8     9     6     6     6
     7    17    12    14     9
    15    14     6     6    10
     4    10     7    10     9
x_star =
  
     0     1     0     0     0
     0     0     0     1     0
     0     0     0     0     1
     0     0     1     0     0
     1     0     0     0     0

    z_star =

    32