算法理解-粒子群算法（一个计算例子）

沿用上一篇中遗传算法的求解例子，其中代码参考游皓麟的R语言预测实战（这是一本好书）：

求解函数

通过下面函数的求解，对粒子群算法进行学习：

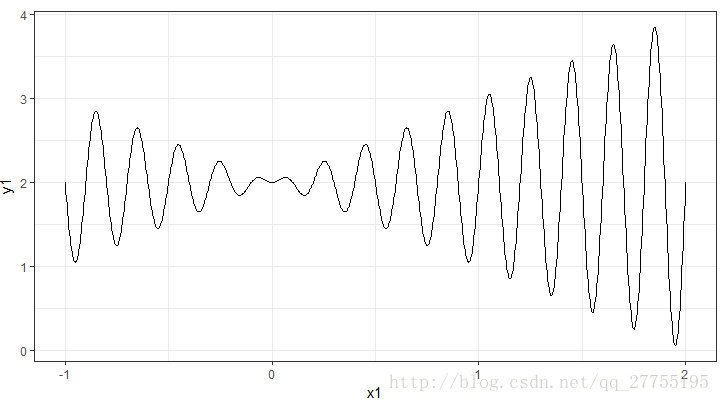
f(x)=x∗sin(10∗π∗x)+2x∈[−1,2]

其函数图像为：

求解流程与概念

原理

鸟（粒子）根据自身经验（自己经过的最高点）、以及所有鸟经验（所有粒子中的最高点）进行探索，每次飞的时间是1(迭代1次)，速度是 v ，这一次飞过的路程 s=v∗1 （x的变化量），假如有奖励就过去，没有就停留在原地，再结合自身经验以及别人的经验思考，下一秒我要怎么飞比较好。
由于每次飞行时间是固定的，因此 位移=速度 ，所以只需要考虑该如何结合其他信息来确定下一秒我飞行的速度。其思考过程用数学公式进行表达则为：

vkid=w∗vk−1id (自身速度惯性)+c1∗r1∗(pbestid−xk−1id) (自身的历史经验)+c2∗r2∗(gbestd−xk−1id) (全部人的历史经验)

还是因为飞行的时间是固定为1的，下一秒我的位置则为：

xkid=xk−1id+vk−1id

从公式中可以看出，速度的更替由3个部分组成惯性，自身经验以及群体经验。在公式中下标 i 表示第 i 个粒子，下标 d 表示第 d 个维度，上标 k 表示当前时刻。则 vkid 表示当前时刻，第i个粒子，第d个维度的速度。其他参数含义：

参数	含义
v	速度
w	为惯性权重，用于记录当前自身的速度，通常为非负数，调节解空间的搜索范围，为0时则失去自身速度的记忆
c1	表示加速度，调节学习的最大步长，当 c1 为0则不考虑自身经验，会导致丧失群体多样性，就是每个点都向当前最高点移动。
c2	表示加速度，调节学习的最大步长、解的搜索空间，当 c2 为0则不考虑其他人的经验，没有信息共享，会导致收敛变慢。
pbest	自身历史经验中的适应度最高的位置信息
gbest	所有粒子历史经验中适应度最高的位置信息

算法流程

1.调节参数以及生成初始粒子群

# 1. 定义求解函数
sloveFun <- function(x){
  x*sin(10*pi * x) + 2
}

#2. 初始化粒子群
limitX <- c(-1, 2) # x限制范围
vmax <- 0.15 * (limitX[2] - limitX[1])  # 速度变化范围为x定义域的15%
particleNum <- 20 # 粒子个数
pbest <- NULL
gbest <- NULL
gbestAdd <- NULL
w <- 1          # 设置惯性权重
c1 <- c2 <- 2   # 设置加速度常数
iters <- 10000  # 设置最大迭代次数
alpha <- 0.0002 # 设置最佳适应度值的增值阈值

#-- 在给定定义域内，随机生成位置矩阵
xMat <- matrix(c(x = runif(particleNum, limitX[1], limitX[2])), dimnames = list(NULL, c("x")))
#              x
# [1,]  1.0536155
# [2,] -0.9237345
# [3,] -0.1517228
# [4,] -0.6818320
# [5,]  1.7338915

#-- 在给定定义域内，随机生成速度矩阵
vMat <- matrix(c(x = runif(particleNum, -vmax, vmax)),  dimnames = list(NULL, c("x")))
#                x
# [1,] -0.43600456
# [2,]  0.17513843
# [3,] -0.03273836
# [4,] -0.24263868
# [5,] -0.01039682

2.计算适应度并初始化pbest\gbest

#3. 计算种群中所有粒子适应度
adjusts <- apply(xMat, 1, sloveFun)
#[1] 3.0468264 1.3732987 1.8484994 2.3683774 0.4834344

#4. 更新迭代pbest\gbest,同时更新所有粒子的位置与速度
pbest <- cbind(xMat, adjusts)
#               x   adjusts
# [1,]  1.0536155 3.0468264
# [2,] -0.9237345 1.3732987
# [3,] -0.1517228 1.8484994
# [4,] -0.6818320 2.3683774
# [5,]  1.7338915 0.4834344

idxAdjusts <- ncol(pbest)
gbest <- pbest[which.max(pbest[, idxAdjusts]),]
#       x  adjusts
# 1.439921 3.368339

3.迭代更新

for (i in 1:iters){
  #4.1 更新pbest
  # ---如果当前位置比之前的位置更适应则替换之前信息
  mapply(function(no, adj){
    if(adj > pbest[no, idxAdjusts]){
      pbest[no, ] <<- c(xMat[no, ], adj)
    }
  }, 1:length(adjusts), adjusts)

  #4.2 更新gbest
  if (max(pbest[, idxAdjusts]) > gbest[idxAdjusts]) {
    gbestAdd <- max(pbest[, idxAdjusts]) - gbest[idxAdjusts]
    gbest <- pbest[which.max(pbest[, idxAdjusts]), ]
    print("--更新gbest")
    print(gbestAdd)
  }

  #4.3 更新所有粒子的位置与速度
  xMatOld <- xMat
  xMat <- xMat + vMat
  vMat <- w*vMat +  # 惯性
    c1 * runif(1, 0, 1) * (pbest[, 1:(idxAdjusts - 1), drop=F] - xMatOld) +    # 自身经验，向自身最优值靠近
    c2 * runif(1, 0, 1) * (matrix(rep(gbest[1:(idxAdjusts - 1)], particleNum), ncol = idxAdjusts - 1 , byrow = T)-xMatOld) # 最优值信息共享

  #4.4 超界修正 
  #---如果vMat有值超过边界值，则设定为边界值
  vMat[which(vMat < (-vmax))] <- (-vmax)
  vMat[which(vMat > (vmax))]  <- (vmax)
  #---如果xMat有值超过边界值，则设为边界值
  xMat[which(xMat < (limitX[1]))] <- (limitX[1])
  xMat[which(xMat > (limitX[2]))] <- (limitX[2])

  #4.5 计算更新候选的种群适应度
  adjusts <- apply(xMat, 1, sloveFun)

  #4.6 检查全局适应度增量，如果小于最佳适应度值的增值阈值，则算法停止
  if (!is.null(gbestAdd) && gbestAdd < alpha) {
    cat("k =", i, "算法结束！")
    cat("\n", "最终结果为：", gbest)
    break()
  }
}

求解结果

相比于遗传算法的测试，PSO在收敛次数上更加不稳定，收敛次数波动较大，少则低于10，多则成百上千。
选取了一个次数较少的，方便动态展示。

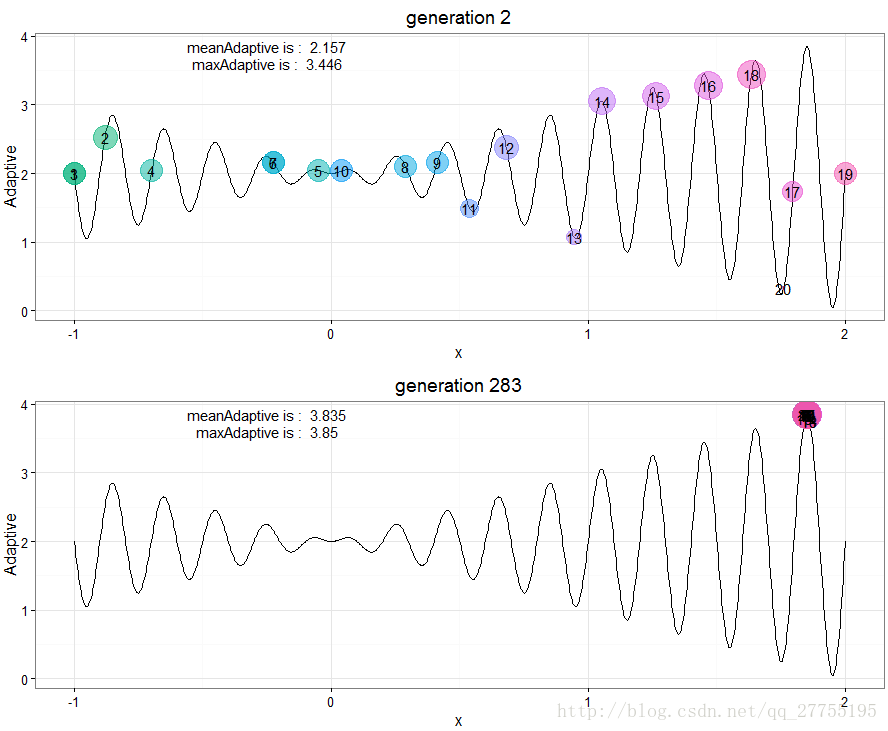
动态过程，无聊的话看着也是挺好玩的：

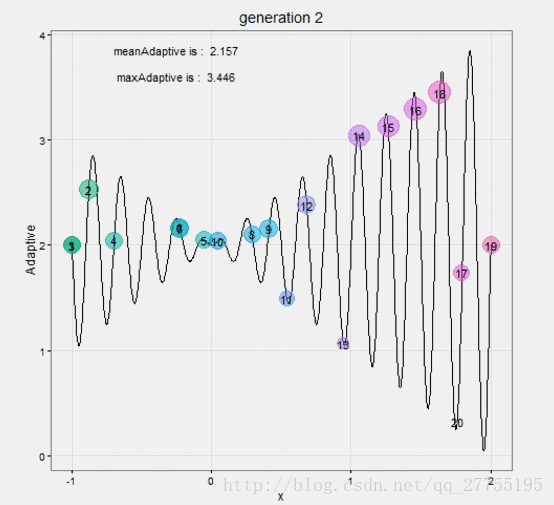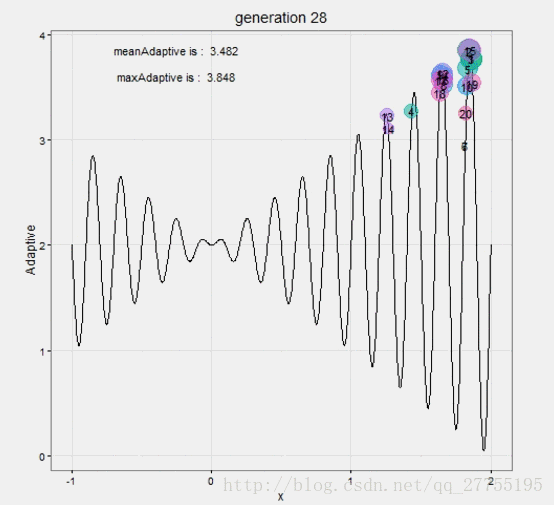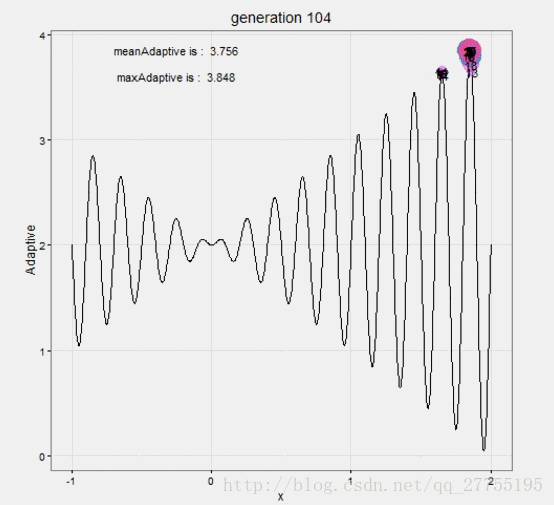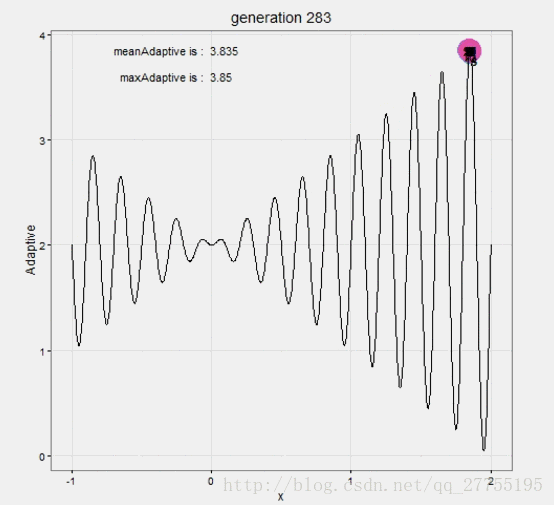
与遗传算法的对比

粒子群算法相比于遗传算法更加的简单易懂，其调节参数较少
不同点：

• PSO由于不需要编码，没有GA算法中由于编码带来的求解精度限制
• 在GA算法中，染色体之间共享信息，所以整个种群的移动是比较均匀地向最优区域移动。PSO中的粒子通过当前搜索到最优点进行共享信息，很大程度上这是一种单项信息共享机制，整个搜索更新过程是跟随当前最优解的过程。在大多数情况下，所有粒子可能比遗传算法中的进化个体以更快速度收敛于最优解。

相似点：

• 它们都是仿生算法，求解过程中存在多个解，因此都可以进行并行运算
• 个体的适配信息进行搜索，因此不受函数约束条件的限制，如连续性、可导性等。

所有代码

# 1. 定义求解函数
sloveFun <- function(x){
  x*sin(10*pi * x) + 2
}

#2. 初始化粒子群
limitX <- c(-1, 2)
vmax <- 0.15 * (limitX[2] - limitX[1])  # 速度变化范围为x定义域的15%
particleNum <- 20
pbest <- NULL
gbest <- NULL
gbestAdd <- NULL
w <- 1          # 设置惯性权重
c1 <- c2 <- 2   # 设置加速度常数
iters <- 10000  # 设置最大迭代次数
alpha <- 0.0002 # 设置最佳适应度值的增值阈值

#-- 在给定定义域内，随机生成位置矩阵
xMat <- matrix(c(x = runif(particleNum, limitX[1], limitX[2])), dimnames = list(NULL, c("x")))

#-- 在给定定义域内，随机生成速度矩阵
vMat <- matrix(c(x = runif(particleNum, -vmax, vmax)),  dimnames = list(NULL, c("x")))

#3. 计算种群中所有粒子适应度
adjusts <- apply(xMat, 1, sloveFun)

#4. 更新迭代pbest\gbest,同时更新所有粒子的位置与速度
pbest <- cbind(xMat, adjusts)
idxAdjusts <- ncol(pbest)
gbest <- pbest[which.max(pbest[, idxAdjusts]),]

for (i in 1:iters){
  #4.1 更新pbest
  #遍历adjusts,如果对应粒子适应度是历史最好的，则完成替代
  mapply(function(no, adj){
    if(adj > pbest[no, idxAdjusts]){
      pbest[no, ] <<- c(xMat[no, ], adj)
    }
  }, 1:length(adjusts), adjusts)

  #4.2 更新gbest
  if (max(pbest[, idxAdjusts]) > gbest[idxAdjusts]) {
    gbestAdd <- max(pbest[, idxAdjusts]) - gbest[idxAdjusts]
    gbest <- pbest[which.max(pbest[, idxAdjusts]), ]
    print("--更新gbest")
    print(gbestAdd)
  }

  #4.3 更新所有粒子的位置与速度
  xMatOld <- xMat
  xMat <- xMat + vMat
  vMat <- w*vMat +  # 惯性
    c1 * runif(1, 0, 1) * (pbest[, 1:(idxAdjusts - 1), drop=F] - xMatOld) +    # 自身经验，向自身最优值靠近
    c2 * runif(1, 0, 1) * (matrix(rep(gbest[1:(idxAdjusts - 1)], particleNum), ncol = idxAdjusts - 1 , byrow = T)-xMatOld) # 最优值信息共享

  #4.4 超界处理  
  #---如果vMat有值超过边界值，则设定为边界值
  vMat[which(vMat < (-vmax))] <- (-vmax)
  vMat[which(vMat > (vmax))]  <- (vmax)
  #---如果xMat有值超过边界值，则设为边界值
  xMat[which(xMat < (limitX[1]))] <- (limitX[1])

  #4.5 计算更新侯的种群适应度
  adjusts <- apply(xMat, 1, sloveFun)

  #4.6 检查全局适应度增量，如果小于最佳适应度值的增值阈值，则算法停止
  if (!is.null(gbestAdd) && gbestAdd < alpha) {
    cat("k =", i, "算法结束！")
    cat("\n", "最终结果为：", gbest)
    break()
  }
}

其他求解方法

遗传算法：http://blog.csdn.net/qq_27755195/article/details/56597467
模拟退火：http://blog.csdn.net/qq_27755195/article/details/62505046