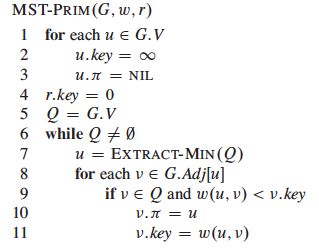最小生成树问题（Minimum Spanning Trees, MST）

最小生成树问题（Minimum Spanning Trees, MST）

作者：Bluemapleman([email protected])

麻烦不吝star和fork本博文对应的github上的技术博客项目吧！谢谢大家的支持！

知识无价，写作辛苦，欢迎转载，但请注明出处，谢谢！

---

问题定义

给定一个无向图G=(V, E)，以及边（Edge）上的权值w: E -> R。

在G中找到一棵生成树$T\subseteq E$，这棵树连接了所有的顶点，且其所有边的权值的总和是所有这样的生成树中最小的。

生成MST的方法

生成MST的两个经典算法Kruskal和Prim算法都是基于贪心的思想，只是它们应用贪心的方式不太一样。但是它们都遵循一个一般性方法（Generic Method），这个一般性方法每次为MST找一个边。这个一般性方法会维持一个边的集合A，并保持以下迭代不变性质(loop invariant)：

每次迭代之后， A是某个MST的边子集。

每一次迭代过程中，我们确定一个可以加到A中，且不违反迭代不变性质的边(u,v)；也就是说，$A\bigcup (u,v)$也是MST的一个子集，我们叫这样的边为安全边（safe edge），因为我们可以在保持迭代不变性质的前提下，把这个边安全地加入到A中。

而找安全边，有以下一个定理可以让我们参考，

G=(V, E)是一个连通的无向图，且它的每个边都有一个相应的权值。A是边的集合E的一个子集，它是G的最小生成树的一个部分。让(S,V-S)称为G的一个划分，若有一条权值最小的边(u,v)横跨划分的两个部分，那么这个边就是一个安全边。

具体证明可参照[1]的23.1节，此处不展开。

而实际的Kruskal与Prim算法的具体差异，实际上就体现在找安全边的思路上。

Kruskal

Kruskal的本质是并查集（Union Find）的应用，而并查集的知识可以参考这篇文章并查集(Union-Find)算法介绍。

• 伪代码

第2、3行：Kruskal首先构造并查集的初始集合，即让每个顶点都的父亲指针都指向自己。

第4行：对G中的所有边按照权值从小到大进行排序。

第5、6、7行：按照权值从小到大顺序遍历每个边，如果当前边的两个顶点不属于同一个集合，则将它们连接起来。

• 示例（来自[1]的23.3节）

• 时间复杂度

  • 对边按照权值排序： O(ElgE)
  • 联合与查找：O(ElgV)

总时长：O(ElgV) (因为$V-1\le E\le C_n^2\le V^2$，所以lgE=O(lgV)，所以O(E(lgE+lgV)=O(ElgV))

Prim

Prim算法则利用一个优先队列（Priority Queue）来存储所有尚未加入到生成树T中的G的顶点，顶点的优先级由连接T与该顶点的权重最小的边的权重决定。

• 伪代码

第1、2、3行：初始化G中所有除T的起始点之外其它顶点的键值（即优先队列中的优先级）。并将结点的父亲指向空。

第6、7行：开始循环，直到优先队列为空，每次循环都从Q中取出优先级最低的那个顶点。

第8、9、10、11行：遍历提取出的顶点的每个相邻边，看该相邻边的权值是否小于边的另一个顶点的键值，若小于，则更新键值为边的权值，并将父亲指针指向提取出的顶点。

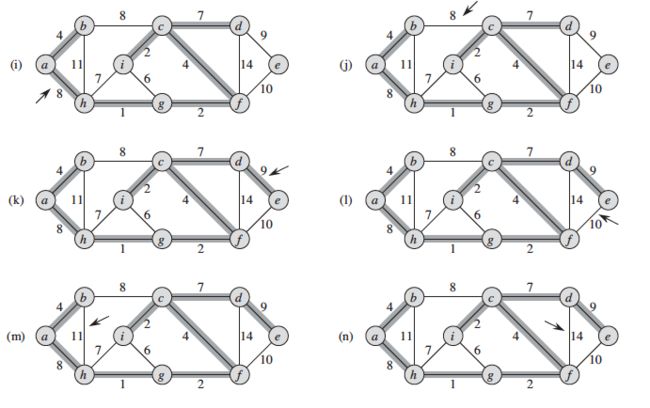
• 示例（来自[1]的23.3节）

• 时间复杂度

优先队列操作：

insert(v)：V次

extractMin()：V次

decreaseKey(v)：E次

假设我们用一个二叉堆来实现优先队列，那么extractMin()与decreaseKey(v)都将是O(lgV)的复杂度。

总时间：

O(VlgV+ElgV)=O(ElgV) (与Kruskal一样)

• *扩展

如果用斐波那契堆(Fibonacci Heap，参考[1]第19章)来实现优先队列，可以实现均摊insert(v)与decreasekey()操作O(1)的时间复杂度。

此时，Prim算法的总的时间复杂度变成了：O(VlgV+E)，比基于二叉堆优先队列实现的Prim性能更好。

参考文献

[1] Introduction to Algorithm: Third Edition, Thomas et al.