堆 与 make_heap(), pop_heap(), push_heap() 与 priority_queue

(转载自很多博客)

https://www.cnblogs.com/chenweichu/articles/5710567.html

https://blog.csdn.net/zsc2014030403015/article/details/45872737

https://www.jianshu.com/p/d174f1862601?utm_campaign=haruki&utm_content=note&utm_medium=reader_share&utm_source=weixin

目录

 

1、堆

2、堆与二叉搜索树

3、堆的插入和删除

3、c++里实现堆的几个方法

4、引申真题

5、使用Python实现堆的构建，并且实现堆排序

---

1、堆

堆（英语：heap)是一类特殊的数据结构的统称。堆通常可以被看做一棵树的数组对象。是非线性数据结构，相当于一维数组。

堆就是用数组实现的二叉树，所有它没有使用父指针或者子指针。堆总是满足下列性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；

• 堆总是一棵完全二叉树。

堆分为两种：最大堆和最小堆，两者的差别在于节点的排序方式。在最大堆中，父节点的值比每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”，并且这个属性对堆中的每一个节点都成立。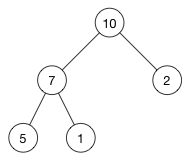上图是一个最大堆。可以看出最大堆的根节点就是这些节点中的最大值。所以堆可以用作优先队列使用，队列中先出现的其实就是最大/最小的值。但是要注意的是！top是最大或最小值，最后一个值不一定是最小/大值。我们只能确定最小/大值是叶子节点中的一个但是不知道是哪个。

2、堆与二叉搜索树

二叉搜索树是一种排序好的树，其左子树的值一定小于根，根一定小于右子树的值。

但是这两者首先排序方式不同，其次数据结构本身就不同。而且堆仅仅用数组表示树的结构可以大幅度降低内存使用，但是树的结构受限。

二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到O(log n)。堆中实际上不需要整棵树都是有序的。我们只需要满足对属性即可，所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证O(log n) 的性能。（插入删除）

在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。（查找）

总之堆适合找当前最大的数和最小的数。

3、堆的插入和删除

(下面我们都假设数组第一个数是1)

3.1插入、建堆

当我们有一个无序序列，99、5、36、7、22、17、46、12、2、19、25、28、1和92,把他们建成一个最小堆。堆是用数组存储。所以我们这里就不用树状图表示过程，直接使用数组。

首先定义一个数组a[14]。之后把第一个数放进去[_,99]。n=1 i=n, while(i!=1) {} else 加入下一个点

之后5进来。n=2 i=n【_,99，5】。while(i!=1) {if(a[i/2]>a[i]) swap(a[i/2],a[i]); i=i/2 }else 加入下一个点  //所以[_,5,99]

之后36进来。n=3 i=n [_,5，99，36] 。while(i!=1) {if(a[i/2]>a[i]) swap(a[i/2],a[i]);else {break;}   i=i/2 }else 加入下一个点 //所以[5,99,36]

之后7进来。n=4 i=n [_,5，99，36，7] 。i=4,a[i/2]=99 99>7 所以交换得到[_,5,7,36,99]。i=2.a[i/2]=5 5<7break;

之后22进来。 n=5 i=n [_,5,7,36,99,22]。i=5,a[i/2]=7 7<22，break.

之后17进来。n=6 i=n [_,5,7,36,99,22,17]。i=6,a[i/2]=36 36>17，所以交换得到[_,5,7,17,99,22,36]。i=3.a[i/2]=5 5<17break;

之后46进来。n=7 i=n [_,5,7,17,99,22,36,46]。i=7,a[i/2]=36 17<46，break;

之后12进来。n=8 i=n [_,5,7,17,99,22,36,46,12]。i=8,a[i/2]=99 99>12，所以交换得到[_,5,7,17,12,22,36,46,99].i=4.a[i/2]=7 7<12 break;

之后2进来。n=9 i=n [_,5,7,17,12,22,36,46,99,2]。i=9,a[i/2]=12 12>2，所以交换得到[_,5,7,17,2,22,36,46,99,12].i=4,a[i/2]=7 7>2 所以交换得到 [_,5,2,17,7,22,36,46,99,12]i=2 a[i/2]=5 5>2 所以交换得到 [_,2,5,17,7,22,36,46,99,12]

之后19进来。n=10 i=n [_,2,5,17,7,22,36,46,99,12,19]。i=10 a[i/2]=22 ,22>19,所以交换得到[_,2,5,17,7,19,36,46,99,12,22] i=5 a[i/2]=5 5<19 break 

之后25进来。n=11 i=n [_,2,5,17,7,19,36,46,99,12,22,25]。i=11 a[i/2]=19 19<25,break

之后28进来。n=12  i=n [_,2,5,17,7,19,36,46,99,12,22,25,28]。i=12 a[i/2]=36 36>28,所以交换得到[_,2,5,17,7,19,28,46,99,12,22,25,36] i=6 a[i/2]=17<28 break.

之后1进来。n=13  i=n [_,2,5,17,7,19,28,46,99,12,22,25,36,1] i=13 a[i/2]=28>1,所以交换得到[_,2,5,17,7,19,1,46,99,12,22,25,36,28] i=6 a[i/2]=17>1,所以交换得到[_,2,5,1,7,19,17,46,99,12,22,25,36,28] i=3 a[i/2]=2>1,所以交换得到[_,1,5,2,7,19,17,46,99,12,22,25,36,28]

之后92进来。n=14  i=n [_,1,5,2,7,19,17,46,99,12,22,25,36,28,92] i=14 a[i/2]=46<92 break

所以最终得到最小堆[1,5,2,7,19,17,46,99,12,22,25,36,28,92]

3.2删除堆节点。

删除当前的最小值。[1,5,2,7,19,17,46,99,12,22,25,36,28,92]，及去掉1.方法是把第一个数1替换成序列的最后一个值，之后进行判断是不是最小堆。得到[92,5,2,7,19,17,46,99,12,22,25,36,28]

。所以对于i=1，首先去看a[i*2]和a[i*2+1]谁小，再判断小的那个是不是比a[i]小，如果小则小的那个是新的a[i]。j=a[i*2]

对于i=1 a[i*2]=5>a[i*2+1]=2,j=3,且2<92,则交换得到[2,5,92,7,19,17,46,99,12,22,25,36,28,92]，i=3

i=3,a[i*2]=17

i=6,a[i*2]=36>a[i*2+1]=28,j=13,且28<92，交换得到[2,5,17,7,19,28,46,99,12,22,25,36,92]，i=13

while(i*2<=14) {执行上述内容}结束，最终得到结果[2,5,17,7,19,28,46,99,12,22,25,36,92]

3、c++里实现堆的几个方法

1、 make_heap(), pop_heap(), push_heap()，sort_heap();

STL中并没有把heap作为一种容器组件，heap的实现亦需要更低一层的容器组件（诸如list,array,vector）作为其底层机制。Heap是一个类属算法，包含在algorithm头文件。

void make_heap(first_pointer,end_pointer,compare_function);一个参数是数组或向量的头指针，第二个向量是尾指针。第三个参数是比较函数的名字。在缺省的时候，默认是大跟堆。把这一段的数组或向量做成一个堆的结构。范围是(first,last)

void pop_heap(first_pointer,end_pointer,compare_function);不是真的把最大（最小）的元素从堆中弹出来。而是重新排序堆。它
把first和last交换，然后将[first,last-1)的数据再做成一个堆。
void pushheap(first_pointer,end_pointer,compare_function);假设由[first,last-1)是一个有效的堆，然后，再把堆中的新元素加
进来，做成一个堆。
void sort_heap(first_pointer,end_pointer,compare_function);作用是sort_heap对[first,last)中的序列进行排序。它假设这个序列是有效堆。（当然经过排序之后就不是一个有效堆了）

例子：

int i,number[20]={29,23,20,22,17,15,26,51,19,12,35,40};

make_heap(&number[0],&number[12]);//结果是:51 35 40 23 29 20 26 22 19 12 17 15 ，默认大堆

make_heap(&number[0],&number[12],cmp);//cmp自己重写，//结果：12 17 15 19 23 20 26 51 22 29 35 40

number[12]=8; push_heap(&number[0],&number[13],cmp);//结果：8 17 12 19 23 15 26 51 22 35 40 20

pop_heap(&number[0],&number[13],cmp);//结果：12 17 15 19 23 20 26 51 22 29 35 40

sort_heap(&number[0],&number[12],cmp);//前提：number已经是一个堆，不然会出错！结果是排序后的，这个时候就不是一个有效堆了

2、priority_queue 本质是一个堆。

头文件是#include

priority_queue，其中Type 为数据类型，Container为保存数据的容器，Functional 为元素比较方式。Container必须是用数组实现的容器，比如vector,deque等等，但不能用 list。STL里面默认用的是vector。

如果把后面2个参数缺省的话，优先队列就是大顶堆（降序），队头元素最大。

例子1：按照pair的first元素降序，first元素相等时，再按照second元素降序
    priority_queue q;
    for( int i= 0; i< 10; ++i ) q.push(i);
    while( !q.empty() ){
        cout<         q.pop();
    }

例子2：

    priority_queue > coll;
    pair a(3,4);
    pair b(3,5);
    pair c(4,3);
    coll.push(c);
    coll.push(b);
    coll.push(a);
    while(!coll.empty())
    {
        cout<         coll.pop();
    }

例子3：

priority_queue<int, vector<int>, less<int> > p;//小顶堆

priority_queue<int, vector<int>, greater<int> > q;//大顶堆

4、引申真题

剑指offer：

https://www.nowcoder.com/practice/9be0172896bd43948f8a32fb954e1be1?tpId=13&tqId=11216&tPage=4&rp=4&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

来自大佬的方法：

//使用一个大堆和一个小堆，维持大顶堆的数都小于等于小顶堆的数，且两者的个数相等或差1。平均数就在两个堆顶的数之中。

//啊啊啊！！！天才的想法！怎么想出来的

class Solution {
public:
    priority_queue, less > p;
    priority_queue, greater > q;
/*使用堆，一个大堆一个小堆，大堆里所有的数比堆顶都小。小堆里所有的数都比堆顶都大。如果让两个堆的个数保持相同，不相等，只能大堆比小堆多1，那么结果可以确保中位数在大堆的堆顶或者大小堆顶的平均*/
    void Insert(int num)//如果num小于大堆的堆顶，那么放在大堆里。如果num大于小堆的堆顶，那么放小堆里。如果在中间，那么谁的size小放谁里面。放完如果两者size差大于1.那么要调整。把多的那个top放入另一个里面，一直到两者size差小于1.
    {
        if(p.size()!=0 && num<=p.top())
            p.push(num);
         else if(q.size()!=0 && num>q.top())
            q.push(num);
        else{
            if(p.size()<=q.size()) p.push(num);
            else  q.push(num);
        }
        while(p.size()>(q.size()+1))
        {
            int y=p.top();
            p.pop();
            q.push(y);
        }
        while(q.size()>(p.size()+1))
        {
            int y=q.top();
            q.pop();
            p.push(y);
        }
        return ;
    }

    double GetMedian()
    {
        if(p.size()==q.size()) return ((p.top()+q.top())/2.0);
        else if(p.size()>q.size()) return p.top();
        else return q.top();
    }

};

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

注意使用priority_queue的堆，删除的时候只能pop。也就是只能删除最大的元素。那么我们怎么可以让其删除堆里的任一元素呢？ 

https://www.nowcoder.com/pat/5/problem/4110

5、堆删除其中任一元素

使用Heap这样的结构体。其本质是一个大根堆。

struct Heap{ priority_queue q1,q2;
    inline void push(int x){q1.push(x);}
    inline void erase(int x){q2.push(x);}
    inline void pop(){for(;q2.size()&&q1.top()==q2.top();q1.pop(),q2.pop());if(q1.size())q1.pop();}
    inline int top(){for(;q2.size()&&q1.top()==q2.top();q1.pop(),q2.pop());return q1.top();}
    inline int top2(){int val,ret; val=top(),pop(),ret=top(),push(val); return ret;}
    inline int size(){return q1.size()-q2.size();}
};

 q1 存储了当前所有元素（包括未删除元素）q2 存储了 q1 中已删除的元素

push就是向 q1 中 push 一个新的元素

erase这就是这个黑科技的精华了，我们向 q2 中 push 一个元素表示在q1 中它已经被删除了

pop这里就要用到 q2 里面的元素了，如果堆顶的元素已经被 erase 过，那么它此时应该在 q2 中的堆顶

此时我们把两个堆一起 pop 就好了，直到堆顶元素不同或者 q2 没元素了

top这里就是先进行和 pop 中类似的操作，删除已经 erase 的元素，然后取出堆顶

top2有点骚，这个操作可以取出堆中的次大值，而 top3top3 、top4top4 以此类推（虽说不怎么用到）

size：这个就是返回堆大小的，可以知道堆当前真实大小就是 q1 大小减去 q2 大小

6、使用Python实现堆的构建，并且实现堆排序

 

对 序列 50, 16, 30, 10, 60,  90,  2, 80, 70 使用堆排序实现增序排列。

from collections import deque  #双向队列，可以在左侧加数值的队列

def swap_param(L, i, j):
    L[i], L[j] = L[j], L[i]
    return L

def heap_adjust(L, start, end):
    temp = L[start]
    i = start
    j = 2 * i
    while j <= end:#从start开始将她后面的，L/2之前的节点。确保他们都是大堆的类型
        if (j < end) and (L[j] < L[j + 1]):#看当前节点的右子节点是否存在，如果存在那么是否比左子节点大。j保存的是左右节点中数值大的那个数
            j += 1
        if temp < L[j]:#如果当前节点的值比子节点小。那么当前节点等于子节点中大的那个值。
            L[i] = L[j]
            i = j
            j = 2 * i
        else: #否则就退出，因为从后往前排的。如果当前temp比当前子节点大。那么就意味着从start开始都满足大堆。因为后面的也都排好了
            break
    L[i] = temp#当前i指的是从start开始找到的最后一个节点的子节点比temp小的位置。


def heap_sort(L):
    L_length = len(L) - 1  #真正树的长度是len-1
# 对于完全二叉树。我们要判断是否所有点的值都比他的叶子节点大/小。只需判断l/2个。因为对于完全二叉树有;/2个叶子节点
    first_sort_count = int(L_length / 2)
    for i in range(first_sort_count):
        heap_adjust(L, first_sort_count - i, L_length) #构建一个大堆。
# 得到大堆，那么大堆的第1位置上的数就是当前(L, 1, L_length - i) 范围里最大的值。把他与放在第L_length - i位置的数对调。之后对(L, 1, L_length - i-1)再次构建大堆。最后一直到i=L_length-1
    for i in range(L_length - 1):
        L = swap_param(L, 1, L_length - i)
        heap_adjust(L, 1, L_length - i - 1)

    return [L[i] for i in range(1, len(L))]

def main():
    L = deque([50, 16, 30, 10, 60,  90,  2, 80, 70])
    L.appendleft(0)#因为List是从0开始，而对于树来说是从1开始所以，在最左边加一个占位。让树从1开始。  右侧加是append（）
    print (heap_sort(L))#结果输出L增序排列

if __name__ == '__main__':
    main()