NKOJ 2019.5.1五一欢乐赛：Round1

A:

解：

暴力。假设$A,B$分别是下标为奇数和偶数的序列。找出每个序列中出现次数最多。
然后用$n$减去次数之和。
但是题目规定这两个序列的数不能一样，所以需要特判一下。
附上本蒟蒻十分丑陋的代码

#include
using namespace std;
int n;
const int maxn=1e5+5;
typedef pair<int,int> P;
#define x first
#define y second
P a1[maxn],a2[maxn];
int main()
{
	cin>>n;
	int a;
	for(int i=1;i<=n;i++)
	{
		cin>>a;
		if(i&1)
		{		
			a1[a].x++;
			a1[a].y=a;
		}
		else
		{
			a2[a].x++;
			a2[a].y=a;
		}
	}
	sort(a1+1,a1+maxn-4,greater<P>() );
	sort(a2+1,a2+maxn-4,greater<P>() );
	if(a1[1].y!=a2[1].y)cout<<n-a1[1].x-a2[1].x;
	else cout<<n-max(a1[2].x+a2[1].x,a1[1].x+a2[2].x);
	return 0;
}

B:

解：

我们知道使${\sum }_{i=1}^n|a_i-x|$最小的$x$是序列$\{a_i\}$的中位数。
这题要求的是${\sum }_{i=1}^n|a_i-(x+i)|$的最小值。
我们立即注意到：
设$b_i=a_i-i$
则原式为：
${\sum }_{i=1}^n|b_i-x|$
所以$x$为序列$\{b_i\}$的中位数

#include
using namespace std;
const int maxn=2e5+5;
typedef long long  ll;
ll sum;
ll a[maxn];

int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		a[i]-=i;
	}
	sort(a+1,a+1+n);
	ll x;
	if(n&1)x=a[n/2+1];
	else x=(a[n/2]+a[n/2+1])/2;
	for(int i=1;i<=n;i++)sum+=abs(a[i]-x);
	cout<<sum;
	return 0;
}

c

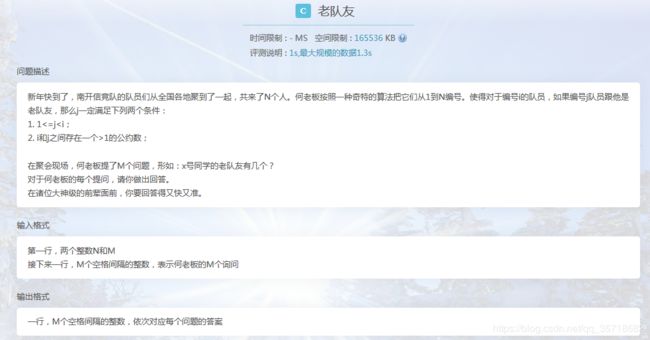
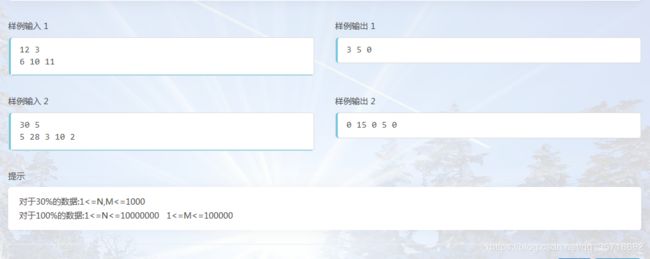
解：

这道很显然是求对于一个数$x$,在$[1,x-1]$中有多少数是与它不互质的。
$[1,x-1]$中与$x$互质的数的个数是$\phi (x)$
$$ans=x-1-\phi (x)$$

#include
using namespace std;
int n,m;
const int maxn=10000000+5;
int phi[maxn];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)phi[i]=i;
	for(int i=2;i<=n;i++)
	{
		if(phi[i]==i)
		{
			for(int j=i;j<=n;j+=i)
			phi[j]=phi[j]/i*(i-1);
		}
	}
	int x;
	for(int i=1;i<=m;i++)
	{
		cin>>x;
		cout<<x-1-phi[x]<<" ";
	}
	return 0;
}

D:

解:

把箭的颜色当做模板，把怪兽的颜色当做文本。
那么第一个问题就是就模板在文本中最大的匹配长度。
很自然地就想到了$KMP$
一边匹配一边记录最大的匹配长度。
第二个问题在记录匹配长度的时候就可以用前缀和算出。

#include
using namespace std;
int n,m;
const int maxn=20000+5;
char A[maxn],B[maxn];
int fail[maxn];
int w[maxn];
int cnt=0,ans;
void kmp()
{
	int j=0;
	for(int i=2;i<=n;i++)
	{
		while(j&&B[j+1]!=B[i])j=fail[j];
		if(B[j+1]==B[i])j++;
		fail[i]=j;
	}
	j=0;
	for(int i=1;i<=m;i++)
	{
		while(j&&B[j+1]!=A[i])j=fail[j];
		if(B[j+1]==A[i])j++;
		if(j>=cnt)
		{
			if(j==cnt)ans=max(ans,w[i]-w[i-j]);
			else ans=w[i]-w[i-j];
			cnt=j;
		}
	}
}

int main()
{
	scanf("%d %d",&n,&m);
	scanf("%s",&B[1]);
	scanf("%s",&A[1]);
	for(int i=1;i<=m;i++)scanf("%d",&w[i]),w[i]+=w[i-1];
	kmp();
	printf("%d %d",cnt,ans);
}

E :

解：

这一题可以用图论知识来做。
如果$|S_i-S_j|>k$,那么在$i,j$之间连一条双向边。
那么最后的答案就是在这个图中，经过所有节点一次的路径有多少条。
考虑一下暴力的$dfs$
可能出现极端情况，图是一个无向完全图。
路径条数最大为$16!$条。显然会$T$
于是考虑优化一下，用记忆化搜索。
设$f[i][s]$表示在$i$号结点把集合$S$中的结点走完的路径条数。
显然可以得到转移方程:
$$f[i][s]=\sum _{k\in S}f[k][S-\{k\}]$$

#include
using namespace std;
typedef long long ll;
#define lowbit(x) (x&-x)
bool g[20][20];
int s[20];
int n,k;
int ans;
ll f[17][1<<16];
int logg[1<<16];
ll dfs(int x,int s)//s中1代表未去过 
{
	if(f[x][s])return f[x][s];
	for(int s1=s,k=lowbit(s1),i=logg[k]+1,s0=s^k;s1;s1^=k,k=lowbit(s1),i=logg[k]+1,s0=s^k)
	if(g[x][i])f[x][s]+=dfs(i,s0);
	return f[x][s];
	
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>s[i],g[0][i]=true,logg[1<<i]=i,f[i][0]=1;
	for(int i=1;i<=n;i++)
	for(int j=i+1;j<=n;j++)
	if(abs(s[i]-s[j])>k)g[i][j]=g[j][i]=true;
	cout<<dfs(0,(1<<n)-1);
	return 0;
}

注：注意本题数据范围。。。。。。。。。。

F:

解：

设有三个顾客$x,x_1,x_2$,送客顺序是$x\to x_1\to x_2$

情况一：
如果$x_1$位于$x$和$x_2$之间，那么不送$x_1$的路程和送$x_1$的路程是一样。或者说：从$x$去送$x_2$的时候顺便把$x_1$送了。

情况二:
如果$x$送完$x_1$后要转向，那么不送$x_1$的路程比送$x_1$的路程少$di{s}_{x\to x_1}\times 2$

那么对于最后一顾客，可以在添加一个位于原点的客户。

#include
using namespace std;
const int maxn=2e5+5;
int a[maxn];
int n,k;
int sum=0;
int w[maxn];
int ans;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{scanf("%d",&a[i]);}
		a[++n]=0;
	for(int i=1;i<=n;i++)ans+=abs(a[i]-a[i-1]);
	for(int i=2;i<=n;i++)
	{
		if((a[i]-a[i-1])*(a[i-1]-a[i-2])<0)w[i-1]=2*min(abs(a[i]-a[i-1]),abs(a[i-1]-a[i-2]));
	}
	for(int i=1;i<=n-1;i++)
	printf("%d\n",ans-w[i]);
	return 0;
	
}