Kaggle竞赛:San Francisco Crime Classification(旧金山犯罪分类) 参赛心得
目录
一、项目概述
二、数据预处理
2.1 特征项
2.3 非数值特征数值化
(1)对category列进行编号
(2)对DayOfWeek列进行编号
(3)对PdDistinct列进行编号
三、特征分析
3.1 按‘year’ 和‘month’ 类型统计
3.2 按‘DayOfWeek’和‘hour’类型统计
3.3 Address列
3.4 经度X和纬度Y
四、 特征选择
4.1 基于单因素变量特征选择
(1)卡方检验:检验定性自变量对定性因变量的相关性
(2)皮尔森相关系数
4.2 平均不纯度减少 (Mean Decrease Impurity)
4.3 平均精确率减少 (Mean Decrease Accuracy)
4.4 特征选择
五、 建立模型
5.1 计算给模型baseline值
5.2 对随机森林模型进行调参
六、 模型优化
6.1 加入新特征:每个地点的犯罪率、每个地点的犯某一种罪的犯罪率
6.2 特征 HourZn, MonthZn, X, Y是否标准化 preprocessing.scale()
6.3 针对特征Y=90进行分析
6.4 特征排序对准确率的影响
(1)基于卡方和皮尔森系数进行特征排序
(2)基于随机森林特征重要性分数进行排序
七、 改进思路
数据源下载:Kaggle旧金山犯罪类型分类San Francisco Crime Classification.zip
下面的所有代码都只是为了说明而放置的一些关键性代码
完整代码和相关论文:https://github.com/455125158/kaggle
一、项目概述
kaggle:
背景:从1934年到1963年,旧金山因高犯罪而臭名昭著。时至今日,旧金山虽以高科技著称于世,但犯罪率扔高居不下。
目的:次数据禁赛提供了近12年整个湾区的犯罪记录,需要我们做的是预测犯罪的类型,对于犯罪把控和警方布置有实际意义。
数据集的时间是:2003-1-1到2015-5-13
数据集包含训练集(大小:22M)和数据集(大小:18.75M)2部分
From 1934 to 1963, San Francisco was infamous for housing some of the world's most notorious criminals on the inescapable island of Alcatraz. Today, the city is known more for its tech scene than its criminal past. But, with rising wealth inequality, housing shortages, and a proliferation of expensive digital toys riding BART to work, there is no scarcity of crime in the city by the bay. From Sunset to SOMA, and Marina to Excelsior, this dataset provides nearly 12 years of crime reports from across all of San Francisco's neighborhoods.
This dataset was featured in our completed playground competition entitled San Francisco Crime Classification. The goals of the competition were to:
predict the category of crime that occurred, given the time and location visualize the city and crimes (see Mapping and Visualizing Violent Crime for inspiration) Content
二、数据预处理
2.1 特征项
This dataset contains incidents derived from SFPD Crime Incident Reporting system. The data ranges from 1/1/2003 to 5/13/2015. The training set and test set rotate every week, meaning week 1,3,5,7... belong to test set, week 2,4,6,8 belong to training set. There are 9 variables:
- Dates - 犯罪事件的时间
- Category - 犯罪事件类别(要预测的目标变量)
- Descript - 犯罪事件的详细描述(只在训练集上)不使用
- DayOfWeek - 星期几
- PdDistrict - 出警的警局名称
- Resolution - 犯罪事件是如何解决的(只在训练集上)不使用
- Address - 犯罪事件的大致街道地址
- X - 经度
- Y - 纬度
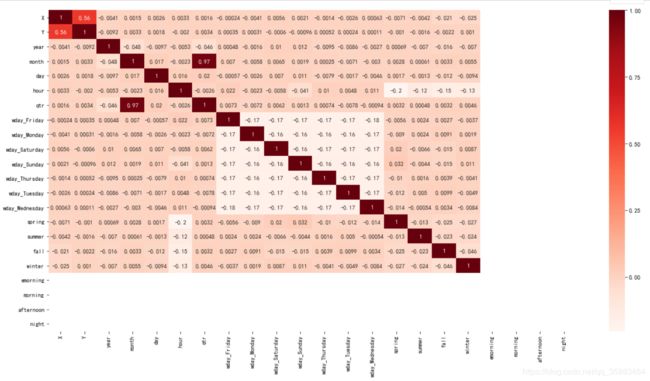
先用热力图看看相关性:
plt.figure(figsize=(20,10))
cor = train.corr()
sns.heatmap(cor, annot=True, cmap=plt.cm.Reds)
plt.show()从图中可以看出,除了X、Y有强相关性,其他特征之间没有回你强的相关性,所以我们只需把X、Y特征当成一个特征即可
2.3 非数值特征数值化
-
(1)对category列进行编号
先看看数据:
# Plot Bar Chart visualize Crime Types
plt.figure(figsize=(14,10))
plt.title('犯罪数量分析')
plt.ylabel('犯罪种类')
plt.xlabel('犯罪数量')
train.groupby([train['Category']]).size().sort_values(ascending=True).plot(kind='barh')
plt.show()由图可知:category分布很不均匀,有的犯罪类型数量多,如LARCENY/THEFT、 OTHER OFFEBSES等;有的犯罪类型数量少,如TREA、 SEX OFFENSES NON FORCIBLE等。
使用one-hot-code列进行编号,再归一化
# one-hot-code
dummy_dayofweef = pd.get_dummies(data['DayOfWeek'],prefix='wday')
data = data.join(dummy_dayofweef)
-
(2)对DayOfWeek列进行编号
还是看看数据:
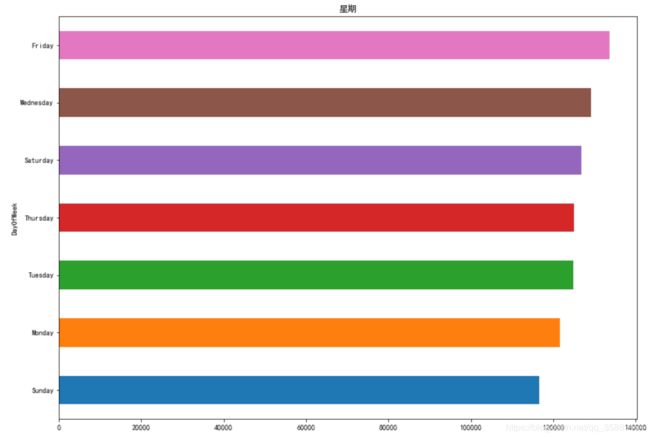
plt.figure(figsize=(14,10))
plt.title('星期')
train.groupby([train['DayOfWeek']]).size().sort_values(ascending=True).plot(kind='barh')
plt.show()还是比较均匀的,对DayOfWeek列进行编号
weekdays = {'Monday':0., 'Tuesday':1., 'Wednesday':2., 'Thursday': 3., 'Friday':4., 'Saturday':5., 'Sunday':6.}
Week = pd.DataFrame([float(weekdays[w]) for w in data.DayOfWeek]) #日期
-
(3)对PdDistinct列进行编号
不同的警局出警次数也不均匀,成功率也不一样,读者可以自己往这方面思考,后面会有这个特征的处理
PdDistrict_Num = pd.DataFrame([float(districts[t]) for t in data.PdDistrict]) #街道编码
三、特征分析
3.1 按‘year’ 和‘month’ 类型统计
可以发现犯罪数量呈季节性变化,夏季和冬季数量少于春季和秋季。 因此我们可以加上 “季节” 特征列。
def getMonthZn(month):
if(month < 3 or month >= 12): return 1; #冬
if(month >= 3 and month < 6): return 2; #春
if(month >= 6 and month < 9): return 3; #夏
if(month >= 9 and month < 12): return 4; #秋
3.2 按‘DayOfWeek’和‘hour’类型统计
周五的犯罪数量最高,可能是因为美国周五party的传统习惯。 周日的犯罪率最低。 因此可以加上 “是否是周末” 特征列。
weekdays2 = {'Monday':0., 'Tuesday':0., 'Wednesday':0., 'Thursday': 0., 'Friday':0.,'Saturday':1., 'Sunday':1}
isWeekday = pd.DataFrame([float(weekdays2[w]) for w in data.DayOfWeek]) #是否是周末凌晨的犯罪数量最低,正午12点和傍晚17、18点犯罪数量最高。因此可以对时间进行时区划分,增加 “时区” 特征列。
def getHourZn(hour):
if(hour >= 1 and hour < 8): return 1;
if(hour >= 8 and hour < 12): return 2;
if(hour >= 12 and hour < 13): return 3;
if(hour >= 13 and hour < 15): return 4;
if(hour >= 15 and hour < 17): return 5;
if(hour >= 17 and hour < 19): return 6;
if(hour < 1 or hour >= 19): return 7;
3.3 Address列
经过统计发现, Address中包含两种地址,一种包含\, 一种包含Block, 并且这两种类型地址交集为空,并集为全部。因此增加 “地址中是否含\” 特征列。
def define_address(addr):
addr_type = 0
if '/' in addr:
addr_type = 1
if 'Block' in addr:
addr_type = 0
return addr_type同时发现, 有22700个不同的地址, 但包含不同数值门牌号的只有135个(没有门牌号的标为0) 。因此可以增加 “门牌号” 特征列。
def Address_Num(addr):
if len(re.findall(r"\d+",addr)) == 0:
addr_num = 0
else:
addr_num = int(re.findall(r"\d+",addr)[0])
return addr_num
3.4 经度X和纬度Y
经度X的范围是[-122.5136421,-120.5];纬度Y的范围是[37.70787902,90],但是除了50个数值为90外,基本上都是37左右。
后续实验思考由于Y=90的值非常少,直接删除。但由于测试集中有16条Y=90的数据,删去后准确率降低,还没有想到更好的办法解决这个问题,因此对这两个特征没有做什么处理,直接使用。
四、 特征选择
4.1 基于单因素变量特征选择
通过比较特征与标签的相关性,与标签相关性高的特征,应当优选选择,也就是排在前面。这种方法比较简单,易于运行,易于理解,通常对于理解数据有较好的效果;但对特征优化、提高泛化能力来说不一定有效。
-
(1)卡方检验:检验定性自变量对定性因变量的相关性
如果你不知道什么事卡方检验看看这篇文章:https://www.jianshu.com/p/807b2c2bfd9b
sklearn官网解释:https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.SelectKBest.html#sklearn.feature_selection.SelectKBest.set_params
from sklearn.feature_selection import SelectKBest, chi2
def squareTest(data):
data = abs(data.values) #dataframe转array
model = SelectKBest(chi2,k=23)
model.fit_transform(data[:,:-1],data[:,-1])
print(model.scores_)
print(model.pvalues_)
-
(2)皮尔森相关系数
一种最简单能帮助理解特征和响应变量之间关系的方法,该方法衡量的是变量之间的线性相关性,结果的取值区间为[-1,1],-1表示完全的负相关,+1表示完全的正相关,0表示没有线性相关
def pearsonTest(data):
print('Year与犯罪类型',pearsonr(data.Year,data.CategoryNum))
print('Month与犯罪类型',pearsonr(data.Month,data.CategoryNum))
print('Day与犯罪类型',pearsonr(data.Day,data.CategoryNum))
print('Hour与犯罪类型',pearsonr(data.Hour,data.CategoryNum))
print('Minute与犯罪类型',pearsonr(data.Minute,data.CategoryNum))
print('Week与犯罪类型',pearsonr(data.Week,data.CategoryNum))
print('isWeekday与犯罪类型',pearsonr(data.isWeekday,data.CategoryNum))
#print('PdDistrict_Num与犯罪类型',pearsonr(data.PdDistrict_Num,data.CategoryNum))
print('BAYVIEW与犯罪类型',pearsonr(data.BAYVIEW,data.CategoryNum))
print('CENTRAL与犯罪类型',pearsonr(data.CENTRAL,data.CategoryNum))
print('INGLESIDE与犯罪类型',pearsonr(data.INGLESIDE,data.CategoryNum))
print('MISSION与犯罪类型',pearsonr(data.MISSION,data.CategoryNum))
print('NORTHERN与犯罪类型',pearsonr(data.NORTHERN,data.CategoryNum))
print('PARK与犯罪类型',pearsonr(data.PARK,data.CategoryNum))
print('RICHMOND与犯罪类型',pearsonr(data.RICHMOND,data.CategoryNum))
print('SOUTHERN与犯罪类型',pearsonr(data.SOUTHERN,data.CategoryNum))
print('TARAVAL与犯罪类型',pearsonr(data.TARAVAL,data.CategoryNum))
print('TENDERLOIN与犯罪类型',pearsonr(data.TENDERLOIN,data.CategoryNum))
print('HourZn与犯罪类型',pearsonr(data.HourZn,data.CategoryNum))
print('MonthZn与犯罪类型',pearsonr(data.MonthZn,data.CategoryNum))
print('Address_Type与犯罪类型',pearsonr(data.Address_Type,data.CategoryNum))
print('Address_num与犯罪类型',pearsonr(data.Address_num,data.CategoryNum))
print('X与犯罪类型',pearsonr(data.Y,data.CategoryNum))
print('Y与犯罪类型',pearsonr(data.X,data.CategoryNum))
4.2 平均不纯度减少 (Mean Decrease Impurity)
利用不纯度可以确定最优条件,通常采用“基尼不纯度”或者“信息增益”.当训练决策树的时候,可以计算出每个特征减少了多少树的不纯度,特征排序可以基于均减少的不纯度的数值,减小的越多,证明该特征排序越前。
这里特征得分采用的是Gini Importance,但是这种方法存在偏向,对具有更多类别的变量会更有利。
对于存在关联的多个特征,其中任意一个都可以作为指示器(优秀的特征),并且一旦某个特征被选择之后,其他特征的重要度就会急剧下降(因为不纯度已经被选中的那个特征降下来了,其他的特征就很难再降低那么多不纯度了,只有先被选中的那个特征重要度很高,其他的关联特征重要度往往较低)。
在理解数据时,这就会造成误解,导致错误的认为先被选中的特征是很重要的,而其余的特征是不重要的,但实际上这些特征对响应变量的作用确实非常接近的。
importances = rfModel.feature_importances_
4.3 平均精确率减少 (Mean Decrease Accuracy)
直接度量每个特征对模型精确率的影响。打乱每个特征的特征值顺序,并且度量顺序变动对模型的精确率的影响。
对于不重要的变量来说,打乱顺序对模型的精确率影响不会太大,但是对于重要的变量来说,打乱顺序就会降低模型的精确率。
所以分数越高,特征越重要,排序越前。
| 伪代码: | 输入:训练数据、训练标签、验证数据、验证标签 输出:特征分数 |
| 1.rf = RandomForestClassifier(参数选择) | |
| 2.rf.fit(train_data,train_label) | |
| 3.rf.predict(test_data) | |
| 4.根据实际模型背景计算正确率accurancy | |
| 5.for i in len(特征) | |
| 6. 打乱每个特征的特征值顺序np.random.shuffle(test_data[:,i]) | |
| 7. rf.predict(test_data) | |
| 8. 计算打乱后的正确率变化shuff_accuracy | |
| 9. 比较改变后正确率的变化 | |
| 10.end | |
| 11.从大到小输出特征的得分 |
4.4 特征选择
经过特征分析、相关性检测和特征重要性打分后,特征选择14列。
| 1 | Year:年,【2003,2015】 |
| 2 | Month:月,【1,12】 |
| 3 | MonthZn:季节,【1,4】 |
| 4 | Day:天,【1,31】 |
| 5 | 67Hour:小时,【0,23】 |
| 6 | HourZn:时区,【1,7】 |
| 7 | Minute:分钟,【0,59】 |
| 8 | Week:星期,【0,6】 |
| 9 | isWeekday:是否是周末,【0,1】 |
| 10 | PdDistrict_Num:街道,【0,9】 |
| 11 | Address_Type:地址类型,【0,1】 |
| 12 | Address_Num:门牌号,【0,134】 |
| 13 | X:经度,【-122.5136421,-120.5】 |
| 14 | Y:纬度,【37.70787902,90】 |
| 15 | Category_Num:犯罪类型,标签,【0,38】 |
同时对训练集进行随机划分为训练集和验证集,比例为4:1。
五、 建立模型
5.1 计算给模型baseline值
由于这是很典型的多分类问题, 因此选择使用朴素贝叶斯、 KNN、 决策树、 随机森林四种算法。由下表可以看到,随机森林的实验结果最好。
| 朴素贝叶斯 | KNN | 决策树 | 随机森林 | |
| 训练集准确率 | 0.23 | 0.24 | 0.21 | 0.29 |
| 测试集准确率 | 0.22 | 0.22 | 0.15 | 0.25 |
5.2 对随机森林模型进行调参
对随机森林模型进行调参。主要对三个参数进行调整,最大特征数max_features、最大深度max_depth和最大迭代数n_estimators
1.首先对最大深度max_depth进行调参,可以看到max_depth=15时测试集准确率最高。
2.在max_depth=15时,对最大特征数max_features 调参,发现无太大区别,思考可能是因为只有14列特征,数量较小。
3.在max_depth=15,max_features = auto时,对最大迭代数n_estimators进行调整,结合算法运行时间和算法准确率,选择n_estimators=200. 因此,犯罪分类模型为RandomForestClassifier(max_depth=15,max_features=auto, n_estimators=200),准确率为0.3028。
六、 模型优化
6.1 加入新特征:每个地点的犯罪率、每个地点的犯某一种罪的犯罪率
具体看代码:
def process_address(train,test):
from copy import deepcopy
# 案发地址集合
addresses = sorted(train['Address'].unique())
# 案发类型集合
categories = sorted(train['Category'].unique())
# 每类案件数量
c_count = train.groupby(['Category']).size()
# 每个案发地址中,每一类案件的发生数量
a_c_count = train.groupby(['Address','Category']).size()
# 每个案发地址的案件数量
a_count = train.groupby(['Address']).size()
# 测试集的案发地址集合
new_addresses = sorted(test['Address'].unique())
# 测试集的每个案发地点的案件数量
new_a_count = test.groupby(['Address']).size()
# 只在测试集中出现的新的案发地址集合
only_new=set(new_addresses+addresses)-set(addresses)
# 同时在测试集和训练集的案发地址集合
in_both = set(new_addresses).intersection(addresses)
# 存放每个地址,发生每一类案件的概率
logodds={}
# 存放每个地址,发生案件的几率
logoddsPA={}
# 最小记录数量
min_counts = 2
# 默认地址发生案件的几率
default_logodds = np.log(c_count/len(train)) - np.log(1.0-c_count/float(len(train)))
# 迭代每一个地址,对logodds和logoddsPA进行填充
# 训练集案发地址
for addr in addresses:
pa = a_count[addr] / float(len(train)) # addr地址的案件数量 / 所有地址案件数量 = addr地址发生案件的概率
logoddsPA[addr] = np.log(pa) - np.log(1-pa)
logodds[addr] = deepcopy(default_logodds)
for cat in a_c_count[addr].keys():
if (a_c_count[addr][cat]>min_counts and a_c_count[addr][cat]
6.2 特征 HourZn, MonthZn, X, Y是否标准化 preprocessing.scale()
分析原因,通过进一步查看数据,发现Y值中大部分数值在37附近,但是有50个数值为90,跨度大,通过preprocessing.scale()后,产生了噪声,导致分类准确度下降
6.3 针对特征Y=90进行分析
由于Y=90时,Category、PdDistrict和Address的取值各种各样,没有规律,训练样本中Y=90有50个,占训练总样本的50/731903=6.83e-05,由于占的比重比较小,所以先考虑直接删除训练集中Y=90的部分。
结果表明,准确率降低。分析原因,发现测试样本中Y=90有16个,占测试总样本的16/146000 = 1.09e-04,如果直接删除训练样本中Y=90的值,丢失掉部分信息。需要进一步分析Y=90与Category之间的关系。
6.4 特征排序对准确率的影响
-
(1)基于卡方和皮尔森系数进行特征排序
可以看到,卡方验证和皮尔森系数结果不是那么好。分析原因可能是因为Pearson相关系数主要是针对回归中的特征分析,
并且作为特征排序机制,只对线性关系敏感。如果关系是非线性的,即便两个变量具有一一对应的关系,Pearson相关性也可能会接近0。
结论: 变量之间存在着关联,不是完全相互独立,所以基于单个变量与标签之间的相关性大小对特征进行排序的效果不好。
-
(2)基于随机森林特征重要性分数进行排序
结论:特征排序对随机森林模型预测准确性没有太大关系。
为了进一步验证特征排列顺序与测试准确率的关系,我们选择了小时/X/Y三个特征,也得到相同的结果。
通过基于树模型得到的特征重要性分数,选取分数最高的三个特征,分钟/X/Y,包含了时间和空间信息,并去其进行全排列,发现正确率没有相近,无明显差异。
目前是基于随机森林树模型,为了验证特征排序是否与模型的结构有关,我们增加了KNN和朴素贝叶斯两种模型。 通过实验结果发现,特征排序对预测结果的影响与模型的选择也无关。
因此,特征的排序对预测结果的影响较小,是因为特征量没有增加,故对预测结果有效的信息量也没有增加。
七、 改进思路
1.增加数据集
《RoboCop:Crime Classification and Prediction in San Francisco》论文正确率为31.84%,方法是在原有数据集上增加了U.S. Census’ ACS API里San Francisco Crime Dataset,从而增加人口统计学demographic特征,提高准确率。(论文在我的GitHub中)
2.使用神经网络模型
3.使用GAN对抗生成网络,增加训练样本