遗传算法及其matlab实现(示例用python库geatpy,matlab遗传工具箱geatbx和lingo三种方式求解)
智能算法是一个边缘交叉学科,有蚁群、粒子群算法、遗传算法、免疫算法、模拟退火等,都乐意算作机器学习的一种类别。
文章目录
- 理论
- 生物理论基础
- 历史
- 算法
- 编解码
- 编码
- 解码
- 染色体交配运算产生子代染色体 crossover
- 基因突变运算产生子代染色体
- 染色体倒位运算产生子代染色体
- 个体适应度评估
- 复制运算
- 示例
- 示例2
遗传算法是模拟达尔文进化论和孟德尔遗传学原理的生物计算模型,是一种模拟自然进化过程以搜索最优解的方法。
理论
生物理论基础
先列出遗传算法中使用到的自然选择的基本观点:(仿佛回到了高二)
-
种群是进化的基本单位
-
进化的实质是种群基因频率的改变
-
基因突变、基因重组、自然选择和隔离是物种形成过程的三个基本环节
突变和重组产生进化的原材料
自然选择使得种群的基因频率定向改变,决定进化方向
隔离是新物种形成的必要条件 -
新物种形成途径有二,渐进式和爆发式,遗传算法中用到了这两种思想。渐进式是通过变异的逐渐积累产生新物种;爆发式是通过杂交和染色体结构变化产生新物种。
历史
1975年,密歇根大学的J.Holland教授提出“遗传算法”的概念。那是最基本的遗传算法原型,现在已有很多变体。
算法
GA包括编解码、遗传运算、个体适应度评估三部分。其中遗传运算包括染色体复制、交叉、变异、倒位。
基因:染色体上的片段,取值0/1
个体:编码后的染色体,个体实际上就是参数的一种离散取值
种群:所有编码后的染色体的集合,参数的一群取值
种群规模一般取 0-100
编解码
编码
有二进制编码和浮点编码两种,但前者便于染色体交叉、变异等用得更多。
若某参数的取值范围是 ( L , U ) (L,U) (L,U), 使用k位二进制编码,则共有 2 k 2^k 2k种编码,所以

容易发现,实际上被编码的是 δ \delta δ的系数,即几个 δ \delta δ。
可以看出编码把参数的连续的取值范围离散化了,这 2 k 2^k 2k个取值就是这个参数的参数空间,是需要被搜索的空间,由于只考虑某些离散的取值,所以k的长度越大,搜索的参数越准确。
解码
解码就是把二进制数串映射回对应的十进制数字,即 ( L , U ) (L,U) (L,U)里那些离散化的取值。
假设编码是 b k b k − 1 ⋯ b 2 b 1 b_kb_{k-1}\cdots b_2b_1 bkbk−1⋯b2b1,则
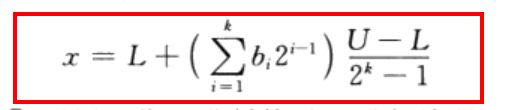
其中括号里main的部分实际上就是这串二进制数对应的十进制数,在这里就是 δ \delta δ的系数。所以解码公式就很容易理解啦,特别简单。
举个栗子
染色体交配运算产生子代染色体 crossover
交配,即单点或多点交叉算子。产生随机数作为一个或多个交配点位置,然后互换基因即可。
如, S 1 = 01001011 , s 2 = 10010101 S_1=01001011,s_2=10010101 S1=01001011,s2=10010101是父代染色体,交换后四位基因,得到子代染色体 S 1 ′ = 01000101 , S 2 ′ = 10011011 S'_1=01000101,S'_2=10011011 S1′=01000101,S2′=10011011

交配概率一般取 0.4-0.99
基因突变运算产生子代染色体
基因突变即 0变1 , 1变0。但概率非常微小,主要是为了避免算法中还没搜索到尽可能多的参数空间,种群就过早收敛,得到不够好的结果。
如父代染色体 S 1 = 01001011 S_1=01001011 S1=01001011的第五位基因突变,得到子代染色体 S 1 ′ = 01000011 S'_1=01000011 S1′=01000011
染色体倒位运算产生子代染色体
染色体某一区段的基因的排列顺序180度颠倒。
如 S 1 = 01011 10110101011 100 S_1=01011~~10110101011~~ 100 S1=01011 10110101011 100的中间区段倒位,
得到子代染色体 S 1 ′ = 01011 11010101101 100 S'_1=01011~~11010101101~~ 100 S1′=01011 11010101101 100
个体适应度评估
这是很重要的一步,对每个个体(参数的一种取值)进行评价,选择适应度高的个体进入下一代的迭代。也就是说,GA依据和个体适应度大小成正比的几率决定当前种群中各个个体遗传到下一代群体的机会。
在优化问题中就是把这个值代进优化表达式运算得到的结果,目标函数就是检测个体适应度的函数。
变异概率一般取0.0001-0.2 (mutation)
复制运算
根据适应度大小决定要不要遗传到下一代。
每个个体遗传到下一次迭代的概率是适应度占的比例,分母是所有个体的总适应度。所以适应度越高的个体被遗传到下一代的概率更大。
P i = f i ∑ k = 1 N f k P_i=\frac{f_i}{\sum_{k=1}^Nf_k} Pi=∑k=1Nfkfi
实现方法:在0到1产生均匀随机数,随机数小于 P i P_i Pi则遗传到下一代。
示例
max f ( x 1 , x 2 ) = 21.5 + x 1 s i n ( 4 π x 1 ) + x 2 s i n ( 20 π x 2 ) \max f(x_1,x_2)=21.5+x_1sin(4\pi x_1)+x_2sin(20\pi x_2) maxf(x1,x2)=21.5+x1sin(4πx1)+x2sin(20πx2)
s . t . { − 3.0 ≤ x 1 ≤ 12.1 4.1 ≤ x 2 ≤ 5.8 s.t.\left\{ \begin{aligned} -3.0\leq x_1\leq12.1\\ 4.1\leq x_2\leq5.8\\ \end{aligned} \right. s.t.{−3.0≤x1≤12.14.1≤x2≤5.8
这是一个连续型决策变量最大化目标的单目标优化问题。
画图代码:
clear all
clc
x1=linspace(-3,12.1,100);
x2=linspace(4.1,5.8,100);
[x1,x2]=meshgrid(x1,x2);
f=21.5+x1.*sin(4*pi*x1)+x2.*sin(20*pi*x2);
mesh(x1,x2,f)
title('f=21.5+x1.*sin(4*pi*x1)+x2.*sin(20*pi*x2)')
xlabel('x1')
ylabel('x2')
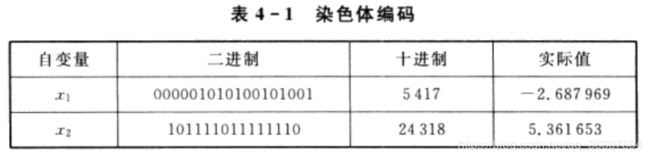
这个最优化问题有两个参数,首先对两个参数编码:
二进制数串的长度(编码位数)取决于要求的精度,如果参数的取值范围是 ( L , U ) (L,U) (L,U),且要求的精度是小数点后4位,则应该至少有 ( U − L ) ∗ 10000 (U-L)*10000 (U−L)∗10000个离散取值,即二进制数串需要表达这么多数字,数串的位数m的计算方法是
2 m − 1 ≤ ( U − L ) × 10000 ≤ 2 m − 1 2^{m-1}\leq (U-L)\times 10000\leq 2^m-1 2m−1≤(U−L)×10000≤2m−1
那么
{ − 3.0 ≤ x 1 ≤ 12.1 ( 12.1 + 3.0 ) ∗ 10000 = 151000 2 m 1 − 1 ≤ ( U − L ) × 10000 ≤ 2 m 1 − 1 m 1 = 18 4.1 ≤ x 2 ≤ 5.8 ( 5.8 − 4.1 ) ∗ 10000 = 17000 2 m 2 − 1 ≤ ( U − L ) × 10000 ≤ 2 m 2 − 1 m 2 = 15 m = m 1 + m 2 = 33 \left\{ \begin{aligned} -3.0\leq x_1\leq12.1\\ (12.1+3.0)*10000=151000\\ 2^{m_1-1}\leq (U-L)\times 10000\leq 2^{m_1}-1\\ m_1=18\\ 4.1\leq x_2\leq5.8\\ (5.8-4.1)*10000=17000\\ 2^{m_2-1}\leq (U-L)\times 10000\leq 2^{m_2}-1\\ m_2=15\\ m=m_1+m_2=33\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧−3.0≤x1≤12.1(12.1+3.0)∗10000=1510002m1−1≤(U−L)×10000≤2m1−1m1=184.1≤x2≤5.8(5.8−4.1)∗10000=170002m2−1≤(U−L)×10000≤2m2−1m2=15m=m1+m2=33
即参数 x 1 , x 2 x_1,x_2 x1,x2分别需要18,15位二进制编码以表示他们的参数空间,则优化模型总共需要33位二进制编码。
下面用三种工具尝试求解这个问题
- LINGO求解:
DATA:
PI=3.14159;
ENDDATA
MAX=21.5+X1*@SIN(4*PI*X1)+x2*@sin(20*PI*X2);
X1<=12.1;
X1>=-3.0;
X2>=4.1;
X2<=5.8;
结果:
Local optimal solution found.
Objective value: 38.73233
Infeasibilities: 0.000000
Extended solver steps: 5
Best multistart solution found at step: 3
Total solver iterations: 42
Elapsed runtime seconds: 0.31
Model Class: NLP
Total variables: 2
Nonlinear variables: 2
Integer variables: 0
Total constraints: 5
Nonlinear constraints: 1
Total nonzeros: 6
Nonlinear nonzeros: 2
Variable Value Reduced Cost
PI 3.141590 0.000000
X1 12.10000 -47.95654
X2 5.725049 0.000000
Row Slack or Surplus Dual Price
1 38.73233 1.000000
2 0.000000 0.000000
3 15.10000 0.000000
4 1.625049 0.000000
5 0.7495092E-01 0.000000
- 用python的geatpy库计算结果:
种群信息导出完毕。
最优的目标函数值为:37.14497969389704
最优的控制变量值为:
11.11465764868793
4.6247291482284005
有效进化代数:25
最优的一代是第 25 代
评价次数:88
时间已过 0.043180227279663086 秒
- matlab的ga遗传工具箱(英国Sheffield大学开发的geatbx),在matlab命令行调出优化工具窗口
>> optimtool
警告: Optimization app will be removed in a future release. See release notes for details.
> In optimtool (line 181)
输入下列参数


由于matlab的工具箱默认优化时最小化,所以目标函数加了负号
function y=MyFunc(x);
y=-(21.5+x(1)*sin(4*pi*x(1))+x(2)*sin(20*pi*x(2)));
注意函数的输入参数只能有一个,所以函数内部要用向量的分量表示每个决策变量
可以看到,三种方式的求解结果相差很小,这是一种很少解决的优化问题。
示例2
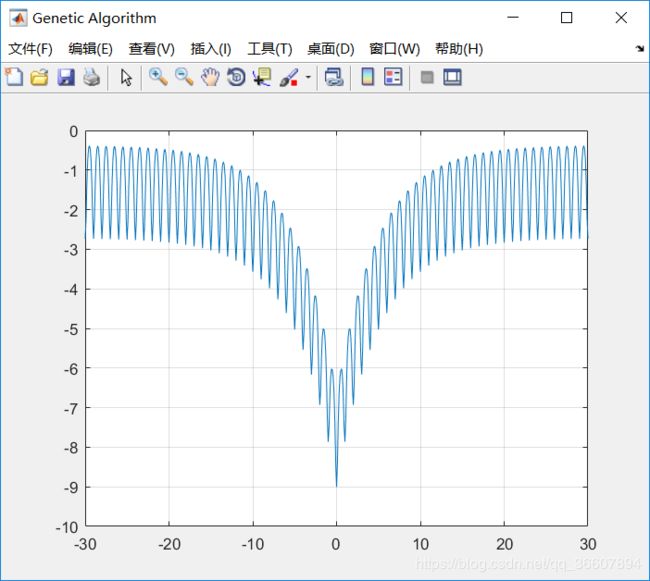
x=-30:.1:30;
N=1;
y=-2*pi*exp(-.2*sqrt((x.^2) / N))-exp((cos(2*pi*x) / N));
plot(x,y)
grid on
x1=-30:.1:30;
x2=-30:.1:30;
N=2;
[x1,x2]=meshgrid(x1,x2);
y=-2*pi*exp(-.2*sqrt((x1.^2+x2.^2) / N))-exp((cos(2*pi*x1)+cos(2*pi*x2)) / N);
mesh(x1,x2,y)
grid on
前面两张图的函数中忘记加2pi了哈,没关系的,后面的图加上2pi,前面就不改了又没什么影响
试试N=10,matlab优化结果,右边栏目的参数都用的默认的,非常接近于自然指数e,最终的10个决策变量取值很多都是0是因为这里显示精度有限
function y=func(x);
N=10;
y=-2*pi*exp(-.2*sqrt((x(1).^2+x(2).^2+x(3).^2+x(4).^2+x(5).^2+x(6).^2+x(7).^2+x(8).^2+x(9).^2+x(10).^2) / N))-exp((cos(2*pi*x(1))+cos(2*pi*x(2))+cos(2*pi*x(3))+cos(2*pi*x(4))+cos(2*pi*x(5))+cos(2*pi*x(6))+cos(2*pi*x(7))+cos(2*pi*x(8))+cos(2*pi*x(9))+cos(2*pi*x(10))) / N)+2*pi;