数据归一化学习笔记
目录
数据归一化的目的:
方法:
代码实现:
Sklearn 中的 Scaler
数据归一化的目的:
由于特征之间的量纲不同,如果直接采用源数据进行机器学习,则不能很好的同时反应各个特征的重要程度;
所以在机器学习前,首先要对数据进行 数据归一化处理,将数据映射到同一尺度。
方法:
1. 最值归一化处理(normalization) :把所有数据映射到 0-1 之间;
适用于数据分布有明显边界的情况;比如一组特征是 考试的分数,分数有明显的边界;
缺点:受outlier(异常值)影响比较大,比如没有明显边界的数据;例如:收入的分布,如果大部分人的收入很少,少部分人的收入非常高,最值归一化处理后,低收入人群的值会被 “挤到” 很小的区域。
2.均值方差归一化(standardization): 把所有的数据归一到均值为0,方差为1的分布中;
适用于数据分布没有明显边界,有可能存在极端数据值;比如收入的分布;
建议:除非数据有明显的边界,一般都使用均值方差归一化。
代码实现:
对于自己编写的代码实现最值归一化的处理可以用下面的代码实现,以二维矩阵 X 为例,分别对每一列套用下面的公式:
X[:,0] = (X[:,0]-np.min(X[:,0]))/(np.max(X[:,0])-np.min(X[:,0]))
X[:,1] = (X[:,1]-np.min(X[:,1]))/(np.max(X[:,1])-np.min(X[:,1]))对于均值方差归一化,以二维矩阵 X2为例,分别对每一列通用下面的公式:
X2[:,0] = (X2[:,0] - np.mean(X2[: ,0]))/ np.std(X2[:,0])
X2[:,1] = (X2[:,1] - np.mean(X2[: ,1]))/ np.std(X2[:,1])Sklearn 中的 Scaler
重要的前提:
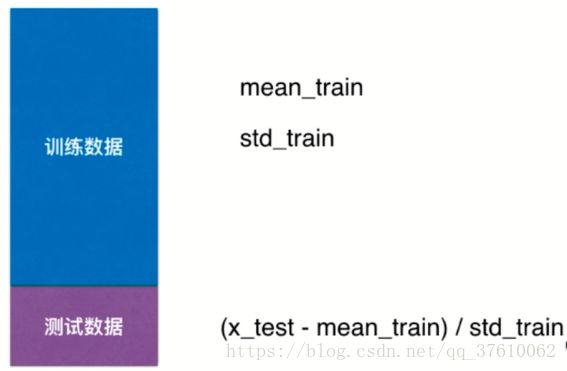
在机器学习中,我们将源数据分为 train 和 test ,对于train 和 test ,显然都要进行数据归一化处理;假设现在要对数据进行均值方差归一化处理;
首先对train进行均值方差归一化处理,之后有一个很重要的点: 对于 test 数据集是进行归一化处理时,同样要使用 train数据集的 均值和方差 ,不能使用 test 数据集的均值和方差!
原因:测试数据集(test)是模拟真实环境
- 真实环境很可能无法得到所有测试数据的均值和方差;比如当 test 数据只有一组数据时 , 是无法计算出均值和方差的
- 对数据的归一化也是算法的一部分;我们由 train 数据集训练模型得到算法,所以train数据集的均值和方差也是 算法中的一部分;
scikit-learn 中的 Scaler:
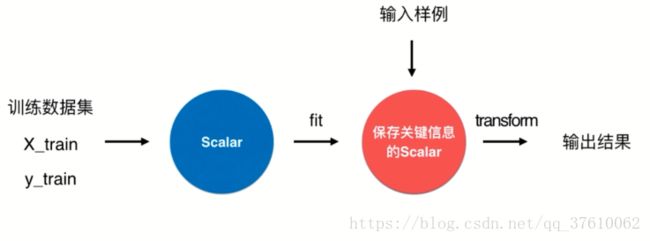
为了保存 train 数据集的均值和方差 ,需要使用scikit-learn 中的 Scaler类 ; Scaler类的封装和 算法的分装模式是一致的;
将 train 数据集传入 Scaler中 进行 fit ,得到一个保存train数据集的各项统计指标的Scaler ,然后将test数据集传入新的Scaler 进行 transform , 得到响应的输出结果。
代码实现:
引入 StandardScaler ,并创建实例
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()对 X_train进行 fit
standardScaler.fit(X_train)
可以通过 standardScaler.scale_ 查看各列的标准差
可以通过 standardScaler.mean_ 查看各列的均值
standardScaler.mean_
standardScaler.scale_此时X_train 并没有被改变,需要进行一次赋值:
X_train_standard = standardScaler.transform(X_train) 对test 进行均值方差归一化处理:
X_test_standard = standardScaler.transform(X_test)最后:sklearn 中也有对 最值归一化处理的 模块; 被封装在 sklearn.preprocessing.MinMaxScaler 中