Linear Regression（线性回归）

线性回归原理：
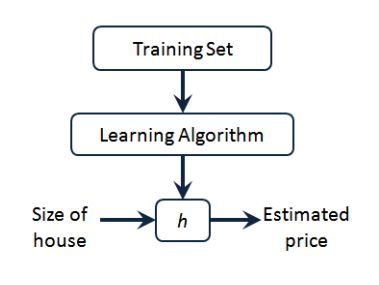
线性回归应该是机器学习最基本的问题了。它是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析，这种函数是一个或多个称为回归系数的模型参数的线性组合，只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。如果数据集中的变量存在线性关系，那么其就能拟合地非常好。

那么如何从一大堆数据里面求出回归方程呢？既然是求“线性回归”，那么我们期望得到：$$h_w(x_1,x_2,...x_n)=w_0+w_1{x}_1+...+w_n{x}_n$$也就是说我们知道了x，y，怎么找到这些w呢？一个常见的方法就是找出使误差最小的w，这里的误差是指预测y和真实y之间的差值，使用该误差的简单累加使得正差值和负差值相互抵消，所以我们一般采用均方误差做它的“代价函数”J：$$J(w_0,w_1...,w_n)=\frac{1}{2}\sum _{i=0}^m(h_w(x_0,x_1,...x_n)-y_i{)}^2$$矩阵写法为：$$J(\mathbf{W})=\frac{1}{2}(\mathbf{X}\mathbf{W}-\mathbf{Y}{)}^T(\mathbf{X}\mathbf{W}-\mathbf{Y})$$
然后求导令其为零可解出即可，这就是最小二乘法。$$\mathbf{W}=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{Y}$$

为什么损失函数前面乘了1/2？
为了在求导的时候，这个系数就不见了，从概率的角度解释有：

• 假设根据特征的预测结果与实际结果有误差E，那么预测结果wx和真实结果y满足下式：
  $$y=W^{T}X+E$$
  设误差E服从正态分布（根据中心极限定理，独立同分布的各变量微小且服从正太分布），那么可知x和y的条件概率：
  

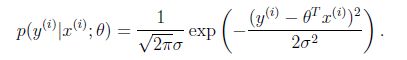
那么每预测一个值就会有一个误差，但概率认为是同一个。所以只需要对这个概率积做最大似然估计求参，求导可得原损失函数。
$$J(\mathbf{W})=\frac{1}{2}(\mathbf{X}\mathbf{W}-\mathbf{Y}{)}^T(\mathbf{X}\mathbf{W}-\mathbf{Y})$$
**补充：利用最小二乘法的矩阵解法对W求导，可得$$X^T(XW-Y)=0$$则要估计的参数$$W=(X^{T}X{)}^{-1}{X}^{T}y$$
此处使用求导公式和链式法则。矩阵的求导一是默认为列向量，二是默认对矩阵所有求导，三是因为是矩阵，所以照搬代数里面的求导是不行的，往往不可乘或者不满足雅各比公式，所以多用转置来解决这种问题，于是就有：$$\frac{\partial }{\partial \mathbf{X}}({\mathbf{X}}^{\mathbf{T}}\mathbf{X})=2\mathbf{X}$$$$\frac{\partial }{\partial \mathbf{W}}(\mathbf{X}\mathbf{W})={\mathbf{X}}^{\mathbf{T}}$$
$$\frac{\partial }{\partial \mathbf{W}}({\mathbf{W}}^{\mathbf{T}}\mathbf{X})=\mathbf{X}$$$$\frac{\partial }{\partial \mathbf{W}}({\mathbf{W}}^{\mathbf{T}}\mathbf{X}\mathbf{W})=2\mathbf{X}\mathbf{W}$$
算法实现：（Python）：

def Regres(X，Y):
    x = mat(X); y = mat(Y).T
    if linalg.det(x.T*x) == 0.0:#判断行列式是否为0
        print ("矩阵行列式为0，不可逆")
        return 0
    else return ((x.T*x).I * (x.T*y))#返回为已经求出的w，其中I为求逆操作

**注：上述函数中的X为便于之后矩阵的运算将偏置值b也纳入X的格式，即X=[[1.0,2.0],[1.0,3.0],[1.0,6.0]]，前一个值恒为偏置值，后一个为x坐标。

矩阵不可逆怎么办？梯度下降法
刚刚推导过程的解可以直接用公式求解，一般这类解叫做解析解（analytical solution）。但是其他大多数算法，特别是深度学习模型往往并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值，这类解叫做数值解（numerical solution）。比如可以用随机梯度下降法来尽可能的线性 逼近，其求解迭代公式为：
$$\mathbf{W}=\mathbf{W}-\alpha {\mathbf{X}}^T(\mathbf{X}\mathbf{W}-\mathbf{Y})$$线性逼近不能知道极值点在什么地方，但是能指引最小极值点的方向，便是“梯度”的含义，其中的$\alpha$是梯度学习的学习率。更多的梯度下降问题在文末补充。

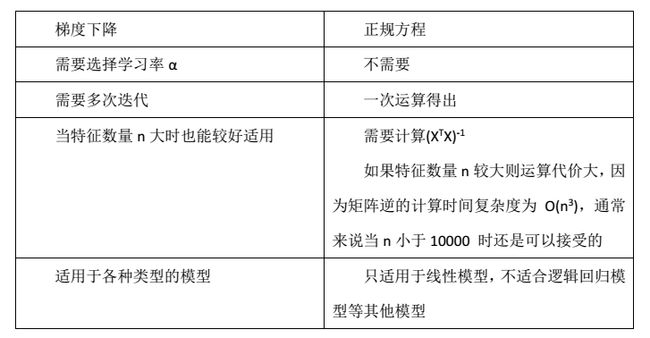
两者有什么区别？辨析梯度下降和正规方程（最小二乘）

最小二乘法需要计算逆矩阵，然而它的逆矩阵可能不存在，无法求解，而此时梯度下降法仍然可以使用。不过如果你想，是可以通过去掉冗余特征使行列式不为0，然后使用的。

拟合结果不满意？欠拟合问题
线性回归很可能会出现欠拟合的现象，局部加权线性回归（Locally Weighted Linear Regression，LWLR），它是一个非参数模型，因为每次进行回归计算都要遍历训练集至少一次。该算法中给待预测点附近的 每一个点（即局部的含义） 都赋予了一点的权重，然后再进行一般的线性回归。参数W计算变为：$$\mathbf{W}=({\mathbf{X}}^{\mathbf{T}}\mathbf{W}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{W}\mathbf{Y}$$
算法实现：（Python）

def lwlr(testPoint,xArr,yArr,k=1.0):#对某点赋予一个权重,k控制指数衰减速度
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]#得到矩阵阶数
    weights = mat(eye((m)))#对角矩阵记录点间权值
    for j in range(m):#更新点间权值
        diffMat = testPoint - xMat[j,:]     
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))#距离越远，权重越小（高斯核）
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print ("This matrix is singular, cannot do inverse")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))#矩阵法计算w
    return testPoint * ws#相乘以该点的返回预测值

def lwlrTest(testArr,xArr,yArr,k=1.0):  #对每个点进行预测
    m = shape(testArr)[0]
    yHat = zeros(m)#初始化预测矩阵
    for i in range(m):#调用lwlr函数遍历每一个点进行预测
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

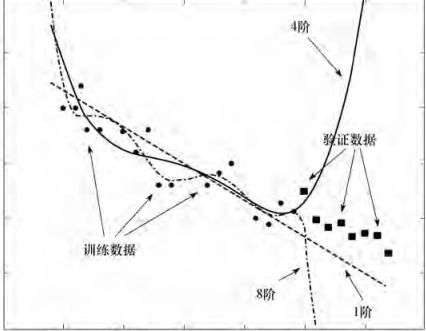
拟合效果不满意？过拟合问题

从上图可以看到不同阶数的选择导致拟合的程度的不同。过拟合则反映的是在学习训练中,对训练集达到非常高的逼近精度,但对非测试集的逼近误差随着训练次数而呈现先下降,后反而上升的奇异现象。

产生原因：迭代次数太多导致拟合了训练数据中的噪声，反而忽略了真实输入输出的关系。

解决方法：过拟合是机器学习所面临的关键障碍，不可避免，只能减少影响。

• 1.丢弃部分特征。（PCA等）
• 2.正则化（Regulation），保留特征，减少参数大小。（注意：0不会不参加任何一个正则化）

L1与L2正则化
正则化其实就是一种对过多回归系数采取惩罚以减少过拟合风险的技术。一般是在原损失函数上加上范数，一般有L0，L1，L2。L0相当于直接限制了参数个数，虽然直观但是不易求解。使用L1范数（也称曼哈顿距离或Taxicab范数，只允许在与空间轴平行行径的距离）又叫lasso回归，损失函数变为：
$$J(\mathbf{W})=\frac{1}{2n}(\mathbf{X}\mathbf{W}-\mathbf{Y}{)}^T(\mathbf{X}\mathbf{W}-\mathbf{Y})+\alpha ||W|{|}_1$$

注意上式因为使用的是L1范数，所以得有样本数n。$\alpha$用于调整惩罚力度，其选择很重要，下图可以看出W和$\alpha$之间的“惩罚”关系：

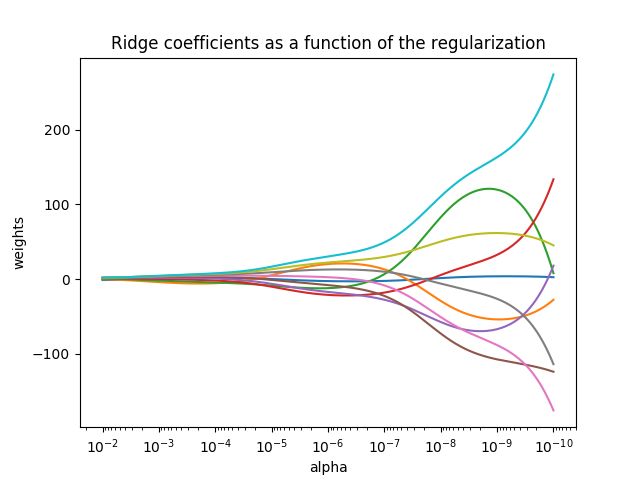
alpha越大时，权重接近0，也更接近于线性变换。
使用L2范数（也称欧几里德距离，是向量到原点的最短距离）又叫ridge回归，损失函数变为：$$J(\mathbf{W})=\frac{1}{2}(\mathbf{X}\mathbf{W}-\mathbf{Y}{)}^T(\mathbf{X}\mathbf{W}-\mathbf{Y})+\frac{1}{2}\alpha ||W|{|}_2^2$$
此时的算法实现变为：（Python）

def ridgeRegres(Xt,Y,lam=0.2):
    denom =X.T*X + eye(shape(X)[1])*lam
    if linalg.det(denom) == 0.0:
        print ("矩阵行列式为0，不可逆 ")
        return
    else return denom.I * (X.T*Yt)

L2的优点是可以限制|w|的大小，从而使模型更简单，更稳定，即使加入一些干扰样本也不会对模型产生较大的影响。而且还能解决非正定的问题，强制使XTX可逆有解。$$\theta =(X{X}^T+\alpha I{)}^{-1}XY$$

L1能使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0，产生稀疏解，起到特征选择的作用，增强模型的泛化能力。

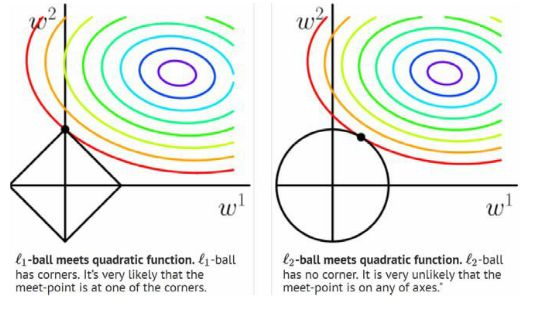
在上图中，两个坐标分别是要学习到的两个参数w1和w2。彩色线是损失函数J的等高线即损失值相等，方形和圆形就分别是L1和L2所产生的额外误差（约束空间），最后的目标要是两者最小，即要得到能使两者相加最小的点，也就是图中的黑色交点。在画等差图时，L1的的效果就很容易与坐标轴相交了，这就是会产生很多0，造成参数稀疏的原因，而且同时如果给一个微小的偏移，L2移动不会很大，而L1可能会移动到方形边上产生很多的交点，这也就是它不稳定的理由了。

l2倾向于w的分量取值更均衡，即非零分量个数尽量稠密，而l0和l1倾向w分量稀疏，即非零分量个数尽量少。所以从图可以看出L1的边缘比较尖锐，与目标函数的等高线相交时，交点会常在那些尖锐的地方，所以很多的参数就是0，即L1能产生稀疏解。所以在调参时如果我们主要的目的只是为了解决过拟合，一般选择L2正则化就够了。但是如果选择L2正则化发现还是过拟合，即预测效果差的时候，就可以考虑L1正则化。另外，如果模型的特征非常多，我们希望一些不重要的特征系数归零，从而让模型系数稀疏化的话，也可以使用L1正则化。

L1正则化损失函数不可微，所以优化方法常用的有坐标轴下降法和最小角回归法。L2可微，所以和普通的求法一样。

前向逐步回归方法
但是它可能会出现处处可导但导数不连续的问题，所以要用前向逐步回归方法（forward stagewise regression）求解。前向逐步回归是一种贪心算法，一开始所有的权重都设为1，然后每一步所做的决策是对某个权重增加或减少一个很小的值。

算法实现（Python）

def regularize(X):#标准化
    inMat = X.copy()
    inMeans = mean(inMat,0) 
    inVar = var(inMat,0) 
    inMat = (inMat - inMeans)/inVar
return inMat

def rssError(yArr,yHatArr): #计算均方误差大小
return ((yArr-yHatArr)**2).sum()

def stageWise(xArr,yArr,eps=0.01,numIt=100):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean 
    xMat = regularize(xMat)
    m,n=shape(xMat)
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
    for i in range(numIt):
        print (ws.T)
        lowestError = inf; 
        for j in range(n):
            for sign in [-1,1]:#增加或减少的影响
                wsTest = ws.copy()
                wsTest[j] += eps*sign
                yTest = xMat*wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        #returnMat[i,:]=ws.T
    #return returnMat

总结一下Regulation的作用：它的出现使函数在数值上更容易求解，在特征数目大时更稳定。通过调节$\alpha$来调配，控制模型的复杂度减小，光滑性更好，复杂性越小且越光滑的目标函数泛化能力越强。系数越小，模型越简单，而泛化能力越强。

对比问题开头提出的两种方法，在单单需要减少过拟合时不建议用PCA，因为它的处理并不考虑任何与结果变量有关的信息，因此可能会丢掉重要的特征，而正则化处理会考虑到结果变量，不会丢失重要的数据。

LR应用：
sklearn里面的Diabetes数据集有442位病人的生理数据以及一年以后的病情发展情况。前十个数据分别表示年龄，性别，体质指数，血压和六种血清的化验数据。

[[ 0.03807591 0.05068012 0.06169621 …, -0.00259226 0.01990842
-0.01764613]
[-0.00188202 -0.04464164 -0.05147406 …, -0.03949338 -0.06832974
-0.09220405]
[ 0.08529891 0.05068012 0.04445121 …, -0.00259226 0.00286377
-0.02593034]
…,
[ 0.04170844 0.05068012 -0.01590626 …, -0.01107952 -0.04687948
0.01549073]
[-0.04547248 -0.04464164 0.03906215 …, 0.02655962 0.04452837
-0.02593034]
[-0.04547248 -0.04464164 -0.0730303 …, -0.03949338 -0.00421986
0.00306441]]

数据归一化处理过，不过这并不影响其代表的信息。

from sklearn import datasets
from sklearn import linear_model

linreg=linear_model.LinearRegression()
diabetes=datasets.load_diabetes()
x_train=diabetes.data[:-20]#前422位做训练集，剩余20做测试集
y_train=diabetes.target[:-20]
x_test=diabetes.data[-20:]
y_test=diabetes.target[-20:]

linreg.fit(x_train,y_train)
print(linreg.predict(x_test))

[ 197.61846908 155.43979328 172.88665147 111.53537279 164.80054784
131.06954875 259.12237761 100.47935157 117.0601052 124.30503555
218.36632793 61.19831284 132.25046751 120.3332925 52.54458691
194.03798088 102.57139702 123.56604987 211.0346317 52.60335674]

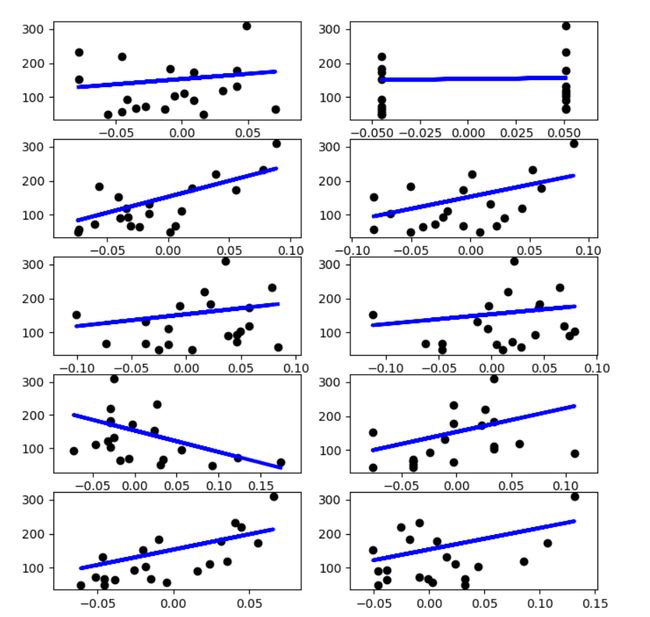
研究单个特征

from sklearn import datasets
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt

linreg=linear_model.LinearRegression()
diabetes=datasets.load_diabetes()
x_train=diabetes.data[:-20]#前422位做训练集，剩余20做测试集
y_train=diabetes.target[:-20]
x_test=diabetes.data[-20:]
y_test=diabetes.target[-20:]
plt.figure(figsize=(8,12))
for f in range(0,10):
    xi_test=x_test[:,f]
    xi_train=x_train[:,f]
    xi_test=xi_test[:,np.newaxis]
    xi_train=xi_train[:,np.newaxis]

    linreg.fit(xi_train,y_train)
    y=linreg.predict(xi_test)
    plt.subplot(5,2,f+1)
    plt.scatter(xi_test,y_test,color='k')
    plt.plot(xi_test,y,color='b',linewidth=3)
plt.show()

用Tensorflow也可以做一个简单的：

import tensorflow as tf
import numpy as np

x_data=np.float32(np.random.rand(2,100))
y_data=np.dot([0.100,0.200],x_data)+0.300

b=tf.Variable(tf.zeros([1]))
w=tf.Variable(tf.random_uniform([1,2],-1.0,1.0))
y=tf.matmul(w,x_data)+b

loss=tf.reduce_mean(tf.square(y-y_data))
optimizer=tf.train.GradientDescentOptimizer(0.5)
train=optimizer.minimize(loss)

init=tf.global_variables_initializer()

sess=tf.Session()
sess.run(init)

for step in range(0,201):
    sess.run(train)
    if step %20==0:
        print (step,sess.run(w),sess.run(b))

其他问题

• 1.普通最小二乘法( Ordinary Least Square,OLS)的回归，在实际运用中可能产生的异方差性（heteroscedasticity）。经典线性回归模型的一个重要假定是：总体回归函数中的随机误差项满足同方差性，即它们都有相同的方差，所以OLS的结果会是线性、无偏、有效估计量。如果不满足，则称线性回归模型存在异方差性。即：
  (1）单调递增型：随X的增大而增大，即在X与Y的散点图中，表现为随着X值的增大Y值的波动越来越大
  (2）单调递减型：随X的增大而减小，即在X与Y的散点图中，表现为随着X值的增大Y值的波动越来越小
  (3）复杂型：与X的变化呈复杂形式，即在X与Y的散点图中，表现为随着X值的增大Y值的波动复杂多变没有系统关系。
  ##此时需要及时检验数据，模型，否则最后的结果将不具有可信性！（常见在金融这种数据干扰源很多的场景）
  ##检测方法：图示，Park和Gleiser检验，Goldfeld-Quandt检验，White检验。

• 2.回归模型中的多重共线性问题。
  即回归模型中使用两个或以上的自变量彼此相关时,则称回归模型中存在多重共线性(multicollinearity)。同样也需要诊断因子再做处理。如方差膨胀因子(Variance Inflation Factor，VIF)，经验判断方法表明:当0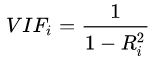
  即变量 i 与其他变量间的关系。或者spearman和pearson相关性系数也可以。

from scipy.stats import pearsonr
from scipy.stats import spearman

pearson(X,Y)
spearman(X,Y)

• 3.线性回归要求因变量服从正态分布？
  在使用线性回归拟合函数时，数据应符合或近似正态分布，否则拟合函数将不正确。原因在于已经提前假设了数据噪声是服从均值为0的正态分布，所以因变量也必须服从时，推导才会成立。

随机梯度下降
普通的梯度计算需要求所有样本的和函数，然后再确定一个梯度最小的方向，在样本量非常大的时候，梯度的计算会非常的耗时。而学习率的选择不恰当也会使梯度要么收敛太慢要么振动太大。

随机梯度法就是为了解决第一个问题；过大的计算量。

• 批梯度下降（GD）：就是一般的梯度下降
• 随机梯度下降（SGD）：每次只使用一个样本进行梯度的计算，可以减少计算，容易跳出局部最小点，在逐渐缩小学习率的情况下收敛速度也跟GD差不多。
• 小批量随机梯度下降（mini batch SGD）：每次使用一批样本进行梯度下降，比SGD更稳定，而且可以利用现有的很多矩阵优化工具，在深度学习上这种方法用的很多。
• 所以更多的优化方法将在深度学习一篇进行整理，包括Momentum、Adagrad、RMSprop和Adam等。

为什么不用牛顿法
牛顿法是利用切线来确定下一次的位置，故也可称为“切线法”。与GD相比，牛顿法是二阶收敛，自然收敛快，而且同样是局部算法，牛顿法会更加的细致，不但考虑了方向还兼顾了移动的步长。

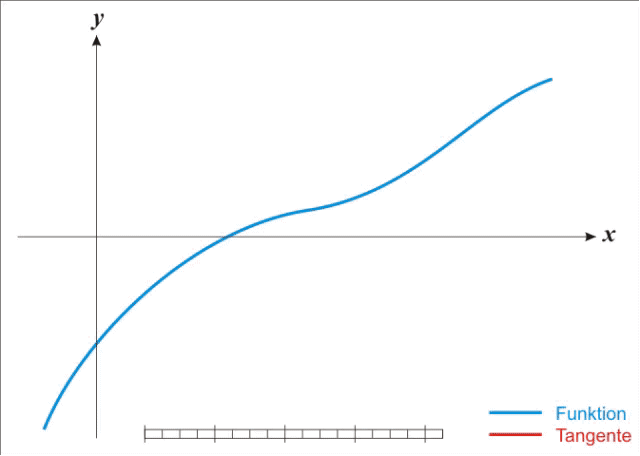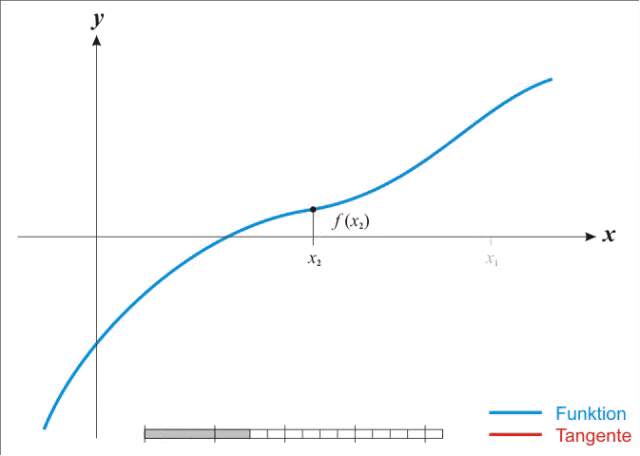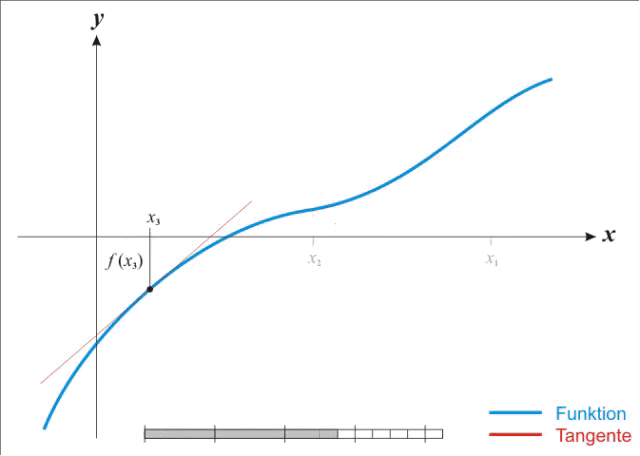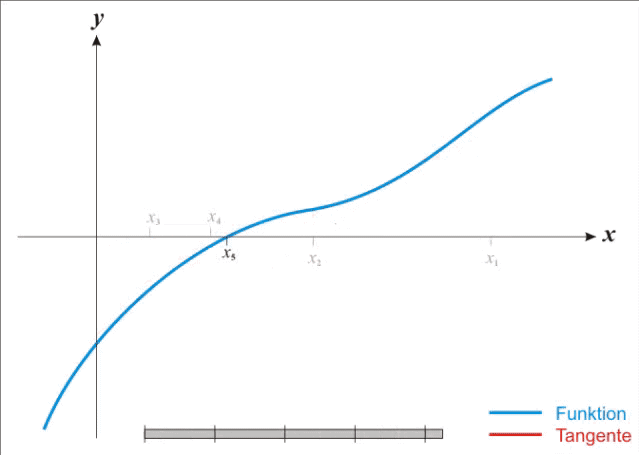
牛顿法要求计算二阶导数即Hessian matrix，在高维度下计算量非常大，而且在小批量训练时，牛顿法对二阶导的估计噪音太大。不过在目标函数非凸时，牛顿法更容易收敛到鞍点或者最大值点。参考wiki的解释是牛顿法是一个用二次曲面去拟合当前位置的局部曲面，相对来说二次曲面要比平面更好，下降路径也自然更好。如下图。

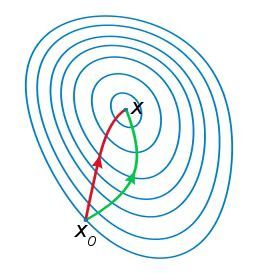
拟牛顿法
使用牛顿法需要的计算量较大，所以为了避免计算二阶矩阵。往往采用DFP算法，BFGS算法等拟牛顿法来求解。

共轭梯度
它介于GD和牛顿法之间，仅需要一阶导，但又克服了GD收敛慢的特点，存储量小，逐步收敛，稳定性高，不需要任何外来参数。是解决大型非线性最优化的最后算法之一，是最后。

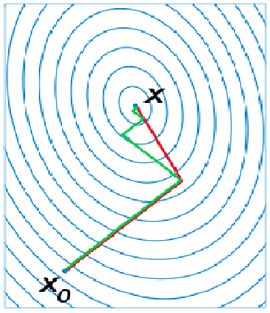
简单来说，它的每一个搜索方向是互相共轭的，而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合，因此，存储量少，计算方便