Dimensionality Reduction（主成分分析PCA与线性判别分析LDA）

PCA原理：

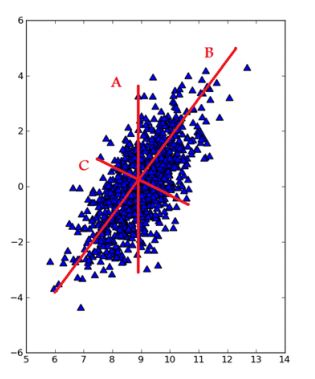
通常情况下，在收集数据集时会有很多的特征，这代表着数据是高冗余的表示，但是对于某个工程来说其实可能并不需要那么多的特征。所以就需要给数据进行降维（Dimensionality Reduction）。降维可以简化数据，使数据集更易使用，降低时间开销，而且能减少一部分噪音的影响，使最后的效果变好。比如上图中，如果进行降维后再进行分类，将会易于处理。
主成分分析（Principal Component Analysis，PCA），顾名思义就是找出最主要的成分来代替就好，那么如何选择最主要的成分来代替能使误差最小呢？即如何选择能最大的代替原来的数据。

PCA的目的就是找到一个方向向量，当我们投影在这个方向上时，希望它的方差尽可能大，均方误差尽可能的小，这样做可以保证所有的点都尽可能的离这条线近。比如在上图，不用想也能明白哪一个方向是最好的。不过这里的均方误差，有必要和线性回归的代价函数做一下比较，一个是投影误差，一个是预测误差。

为了将数据从原来的坐标系转移到了新的坐标系，新的坐标系将由数据本身决定，第一个新坐标是方差最大的方向，其他的是与第一个方向方向正交且具有最大方差的方向。因为发现大部分方差都包含在前几个新坐标中，因此可以忽略余下的坐标轴，从而保证了数据的特征的最小损失。那么可以求出其协方差矩阵来判断。证明一下，如果对于任意一个点$x_i$，可得其在新的坐标系中的投影为$WT{x}_i$，投影方差为$WT{x}_i{x}_i^{T}W$，那么最大化$\sum _{i=1}^m{W}^T{x}_i{x}_i^{T}W$即可。轻松可知$X{X}^{T}W=（-\lambda ）W$。即算出其协方差矩阵就行了，然后保留最重要的几个特征，将数据进行转换降维就完成了。

算法实现：（Python）

def pca(dataMat, topNfeat=9999999):#topNfeat是应用的前N个特征，不指定就返回前999999
    meanVals = mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals #去平均值
    covMat = cov(meanRemoved, rowvar=0)#协方差
    eigVals,eigVects = linalg.eig(mat(covMat))#特征值
    eigValInd = argsort(eigVals)#从小到大排序
    eigValInd = eigValInd[:-(topNfeat+1):-1]
    redEigVects = eigVects[:,eigValInd]#topN的特征向量
    lowDDataMat = meanRemoved * redEigVects#转换新空间
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat

PCA应用：
对如上图所示的iris数据进行降维。
PCA参数说明：
PCA(copy=True, iterated_power=‘auto’, n_components=None, random_state=None,svd_solver=‘auto’, tol=0.0, whiten=False)

copy=True：是否复制
iterated_power='auto'：迭代
n_components=None：降维特征数目
random_state=None：随机状态
svd_solver='auto'：自否采用SVD
tol=0.0：容忍度
whiten=False：是否特征归一化

from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA#导入PCA模块
from mpl_toolkits.mplot3d import Axes3D#绘制3D散点图
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei'] 
mpl.rcParams['axes.unicode_minus'] = False 

iris=datasets.load_iris()

x=iris.data[:,1]
y=iris.data[:,2]
species=iris.target
x_reduced=PCA(n_components=3).fit_transform(iris.data)

fig=plt.figure()
ax=Axes3D(fig)
ax.set_title('基于iris数据集的PCA',size=14)#设置题目
ax.scatter(x_reduced[:,0],x_reduced[:,1],x_reduced[:,2],c=species)

ax.set_xlabel('第一维特征')#设置x轴标签
ax.set_ylabel('第二维特征')
ax.set_zlabel('第三维特征')
ax.w_xaxis.set_ticklabels(())#去除刻度文本，便于观察数据
ax.w_yaxis.set_ticklabels(())
ax.w_zaxis.set_ticklabels(())
plt.show()

PCA的第一主成分与第二主成分
主成分分析本身是要将众多具有相关性的特征，重新组合一下变成新的相互无关的特征组合来代替原来的，主要是研究如何用少数几个主成分来最大可能的揭示变量间的内部结构。F1即通过PCA选取的第一主成分，F1的方差应该是所以特征中最大的，当F1不足以来表达特征时，将考虑第二特征，此时F1所含义的信息不必在冗余出现在F2中，所以要求两者无关，Cov（F1，F2）=0等等，按照这样的思路可以构建多个主成分。

换个角度理解PCA
PCA的目的不就是找个新的基坐标来减少维度（自由度）吗？然后再根据基坐标重建整个数据。那么目标函数就可以变为了要最小化这个重建的误差，然后同样的也可以推导出类似上面方法的目标形式。那么关键是这个视角与第一种的差距在哪呢？可以看出一个是为了找主成分，一个直接进行维度缩减。所以其实从某种角度上来看，这个视角或许才是更适合PCA降维的理解。

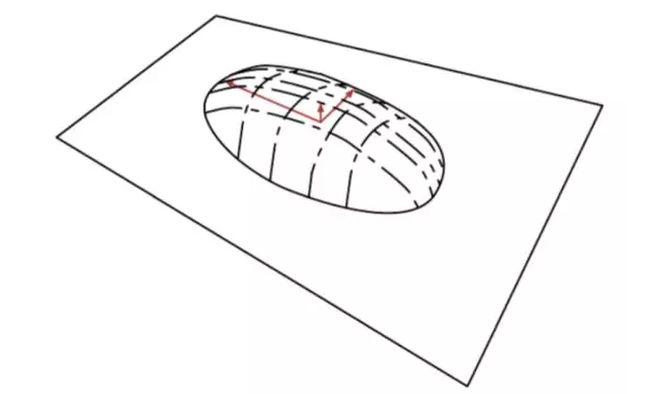
《Deep Learning》一书中打过的比方–烙饼空间（Pancake）， 而在烙饼空间里面找一个线性流行就是PCA的另一种理解，即把数据概率值看成是空间！！。

LDA原理
LDA与主成分分析PCA很像，但不同于PCA寻找使全部数据方差最大化的主坐标轴成分，LDA关心的是能够 最大化类间区分度 的坐标轴成分。即LDA在特征空间投影降维的同时，还能能保持区分类别的信息。 所以在实际应用中LDA降维不仅降低分类任务的计算量，还能减小参数估计的误差，避免过拟合。

为了区分出具体类别需要计算散布矩阵，利用散布矩阵就可以完成降维。具体操作如下：

• 计算中不同类别数据的 n 维均值向量。
• 计算散布矩阵，包括类间、类内散布矩阵。
• 计算散布矩阵的本征向量 e1,e2,…,en 和对应的本征值 λ1,λ2,…,λn。
• 将本征向量按本征值大小降序排列，然后选择前 k 个最大本征值对应的本征向量，组建一个 n×k 维矩阵——即每一列就是一个本征向量。 （丢掉一些并没有那么重要的向量）
• 用这个n×k-维本征向量矩阵将样本变换到新的子空间，即输出降维的结果。这一步可以写作矩阵乘法 Y=X×W 。 X 是 N×d 维矩阵，表示 N 个样本； y 是变换到子空间后的 N×k 维样本。

其中所定义的类内散布矩阵$S_W$:$$S_W=\sum _{i=1}^c{S}_i$$,其中$S_i={\sum }^n(x-m_i)(x-m_i{)}^T,m_i=\frac{1}{n_i}{\sum }^n{x}_k$，即是类内中的每个x减去均值的中心投影，k是期望降维的维度。

类间散布矩阵$S_B$：$$S_B=\sum _{i=1}^c{N}_i(m_i-m)(m_i-m{)}^T$$
使类别间的距离越大越好。

from sklearn import datasets
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D#绘制3D散点图
from pylab import *
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA #导入LDA模块

mpl.rcParams['font.sans-serif'] = ['SimHei'] 
mpl.rcParams['axes.unicode_minus'] = False 

iris=datasets.load_iris()

x=iris.data[:,1]
y=iris.data[:,2]
species=iris.target
x_reduced=LDA(n_components=2).fit_transform(iris.data,species)
print(x_reduced)

fig=plt.figure()
ax=Axes3D(fig)
ax.scatter(x_reduced[:,0],x_reduced[:,1],x_reduced[:,2],c=species)

plt.show()

对比一下PCA的降维结果：

可以很清楚的看到两者的差别。一个是向着最大主成分，一个是注重类别。