频域分析之稳定裕度

本文承接上篇博客奈奎斯特稳定性判据的推导

我们来看频域分析中的非常重要的概念：稳定裕度

首先来看稳定裕度的定义：若$Z=P-2N=0$(其中$P=0$)，则奈奎斯特曲线$G(jw)H(jw)$过$(-1,j0)$点时，系统临界稳定，相频和幅频同时满足条件:

$$\{\begin{array}{l}A(\omega )=1\\ \phi (\omega )=(2k+1)\pi k=0,\pm 1,\pm 2,\cdots \end{array}$$

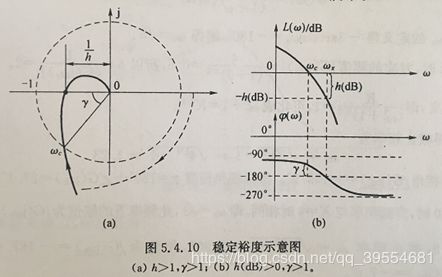
系统远离平衡点的程度，即可用稳定裕度来表示，如下图所示：

Q:为什么穿越$(-1,j0)$点时为临界状态？

A:可以看出，在稳定裕度的定义中假定了$P=0$，即系统的开环正极点数为0，由奈奎斯特稳定性判据，系统的闭环正极点数为$Z=2N$，奈奎斯特曲线逆时针包围$(-1,j0)$点的圈数(沿相角增大方向穿越$(-1,j0)$左半实轴次数)即为闭环正极点数，我们自然想到，若系统奈奎斯特曲线均在$(-1,j0)$点右侧，那么就不存对$(-1,j0)$左半实轴的穿越，闭环系统也就没有正极点了，所以$(-1,j0)$点是系统稳定的临界点，稳定裕度刻画了系统从稳定状态变化到不稳定状态时幅值和相角的”变化程度”；

注意：稳定裕度只对最小相位系统适用，因为在稳定裕度的定义中假定了系统没有开环正极点(这里稍微有些疑惑，最小相位系统是指在$s$右半平面既无零点也无极点的系统，而此处只说明了系统开环传递函数没有正极点)

相角裕度$\gamma$

系统截止频率$w_c$处，幅值满足条件$A\left({\omega }_c\right)=\left|G\left(j{\omega }_c\right)H\left(j{\omega }_c\right)\right|=1$时，若其相角再减小$\gamma$后，将达到临界稳定条件(穿过$(-1,j0)$点)，即：

$$\angle G\left(j{\omega }_c\right)H\left(j{\omega }_c\right)-\gamma =-180^{\circ }$$

所以：

$$\gamma =180^{\circ }+\angle G\left(j{\omega }_r\right)H\left(j{\omega }_c\right)$$

称为相角裕度。

当$\gamma >0$时，系统稳定；当$\gamma =0$时，系统临界稳定；当$\gamma <0$时，系统不稳定。

幅值裕度$h$

设系统的穿越频率为$w_x$，$w_x$满足相角条件

$$\phi \left({\omega }_x\right)=\angle G\left(j{\omega }_x\right)H\left(j{\omega }_x\right)=(2k+1)\pi ,k=0,\pm 1，\pm 2，\dots$$

若幅值再增大$h$倍后，系统达到临界稳定条件，即：

$$h\left|G\left(j{\omega }_x\right)H\left(j{\omega }_x\right)\right|=1$$

可得：

$$h=\frac{1}{\left|G\left(j{\omega }_x\right)H\left(j{\omega }_x\right)\right|}$$

若在对数坐标系下，则：

$$h(\mathrm{d}\mathrm{B})=-20\lg \left|G\left(j{\omega }_x\right)H\left(j{\omega }_x\right)\right|$$

$h$称为幅值裕度。

当$h>1$或者$h>0dB$时，系统稳定；当$h=1$或者$h=0dB$时，系统临界稳定；当$h<1$或者$h<0dB$时，系统不稳定。