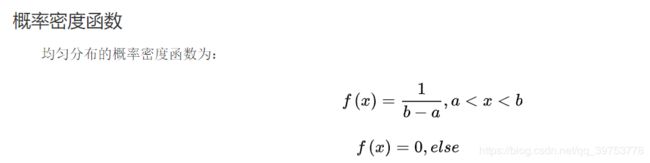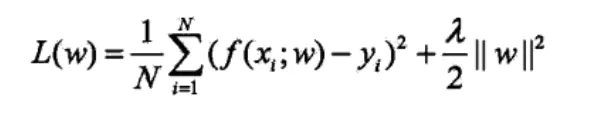数据挖掘习题汇总：线性回归、KNN、K-means、决策树、关联规则

作业清单（4/20）

【1】 安装Python 3.X 和 Orange3 软件，是否完成？

已完成

【2】 完成课堂实验（给定教师数据，判断身份的实验），是否完成？

已完成

data =[ {'NAME':'Mike','RANK':'Assistant Prof', 'YEARS':3, 'TENURED':None},
        {'NAME':'Mary','RANK':'Assistant Prof', 'YEARS':7, 'TENURED':None},
        {'NAME':'Bill','RANK':'Professor', 'YEARS':2, 'TENURED':None},
        {'NAME':'Jim','RANK':'Assistant Prof', 'YEARS':7, 'TENURED':None},
        {'NAME':'Dave','RANK':'Assistant Prof', 'YEARS':6, 'TENURED':None},
        {'NAME':'Anne','RANK':'Assistant Prof', 'YEARS':3, 'TENURED':None}]
for dict in data:
    if dict['RANK']=='Professor' or dict['YEARS']>6:
        dict['TENURED']='yes'
    else:
        dict['TENURED']='no'
    print(dict['NAME'],dict['TENURED'])

【3】 复习Numpy的主要功能（按照课堂PPT完成相关实验）

• 求平均数、中位数、众数，对数组进行排序

  >>> from numpy import mean,median,sort
  >>> from scipy.stats import mode
  >>> a = [1,2,3,4,5,5,6]
  >>> print(mean(a))
  3.7142857142857144
  >>> print(median(a))
  4.0
  >>> print(mode(a)[0])
  [5]
  >>> print(sort(a))
  [1 2 3 4 5 5 6]
  

• 创建矩阵

>>> from numpy import mean,median,sort
>>> b= np.arange(3,15)
>>> b
array([ 3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])
>>> b.reshape(3,4)
array([[ 3,  4,  5,  6],
       [ 7,  8,  9, 10],
       [11, 12, 13, 14]])

• 矩阵排序

• 矩阵相乘

>>> import numpy as np
>>> b = np.arange(12,24).reshape([4,3])
>>> a = np.arange(0,12).reshape([3,4])
>>> p = np.dot(a,b)
>>> p
array([[114, 120, 126],
       [378, 400, 422],
       [642, 680, 718]])
>>>                           

【4】 完成参考教材第1章 1.9的第1题和第4题（抄题）

Problem:

1.1 What is data mining? In your answer, address the following:

(a) Is it another hype?

(b) Is it a simple transformation or application of technology developed from databases,statistics, machine learning, and pattern recognition?

© We have presented a view that data mining is the result of the evolution of database technology. Do you think that data mining is also the result of the evolution of machine learning research? Can you present such views based on the historical progress of this discipline? Address the same for the fields of statistics and pattern recognition.

(d) Describe the steps involved in data mining when viewed as a process of knowledge discovery.

Answer:

(a) No. 数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程

(b) No

© 数据挖掘起始于20世纪下半叶，是在当时多个学科发展的基础上发展起来的。随着数据库技术的发展应用，数据的积累不断膨胀，导致简单的查询和统计已经无法满足企业的商业需求，亟需一些革命性的技术去挖掘数据背后的信息。同时，这期间计算机领域的人工智能也取得了巨大进展，进入了机器学习的阶段。因此，人们将两者结合起来，用数据库管理系统存储数据，用计算机分析数据，并且尝试挖掘数据背后的信息。

模式识别方法也越来越多被应用于数据挖掘。

后来，人们逐渐开始发现数据挖掘中有许多工作可以由统计方法来完成,并认为最好的策略是将统计方法与数据挖掘有机的结合起来.

数据挖掘受到很多学科领域的影响，其中数据库、机器学习、统计学无疑影响最大。简言之，对数据挖掘而言，数据库提供数据管理技术，机器学习和统计学提供数据分析技术。

由于统计学往往醉心于理论的优美而忽视实际的效用，因此，统计学界提供的很多技术通常都要在机器学习界进一步研究，变成有效的机器学习算法之后才能再进入数据挖掘领域。从这个意义上说，统计学主要是通过机器学习来对数据挖掘发挥影响，而机器学习和数据库则是数据挖掘的两大支撑技术。*从数据分析的角度来看，绝大多数数据挖掘技术都来自机器学习领域，但机器学习研究往往并不把海量数据作为处理对象，因此，数据挖掘要对算法进行改造，使得算法性能和空间占用达到实用的地步。*同时，数据挖掘还有自身独特的内容，即关联分析。

Problem：

Present an example where data mining is crucial to the success of a business. What data mining functionalities does this business need (e.g., think of the kinds of patterns that could be mined)? Can such patterns be generated alternatively by data query processing or simple statistical analysis?

Answer:

中国石油天然气集团有限公司利用“魔镜”进行数据挖掘。

首先，魔镜对中石油的供应链业务数据进行了分析，可以使其更合理的监控供应时间、库存、成本、物流、订单所处环节以及所涉及的金额是多少等等。

其次，魔镜还对销售情况进行了分析，方便其了解订单、成交额、成交地区、销售产品种类、销售预测及达标率、成本等情况。

再者，魔镜对中石油的后勤进行了分析，包括交货数、交货天数、订单成交时间、未交订单等，可以通晓不同地区各时间段的购买情况。

第四，魔镜对中石油的客户也进行了分析。魔镜用雷达覆盖的面积从购买周期，平均购买量，忠诚度，平均购买销售额，平均购买创造利润等多个维度来衡量用户整体质量，来看客户的最长、最短和平均购买周期，是稳定的客户还是波动大的代理商或个人暂时出现的周期等，从而分析出哪个区域的客户购买力最稳定，对不同用户进行同时对比，同时展现，综合的分析客户的价值，直接找到短板。最后再对这些用户下一次购买的时间进行预计，报警并及时作出决策。

第五，魔镜从生产线、产品种类、产品状态、库存量、产品质量数量等生产、仓储情况进行了分析。根据魔镜可视化图表，一目就可以了解到每种产品在库存整体占用情况，每笔单子占用多少，其中每种产品又有多少；各个过程有多少损耗；还有各产品在各个区域购买的情况等，最终把这些情况转化成果，知道了哪些品类的产品好卖，又有哪些是滞销产品。

第六，魔镜使中石油的销售额、成本、预算、利润、结余等财务得到精准的分析。直观地了解了每一部分的资金流向问题，资金从哪里来？到哪里去？还印证了借贷必相等的规则。

最后，通过工作绩效、组织架构、员工满意度等方面的分析。从图表可以看出中石油的组织架构全局，每一位员工的KPI销售绩效、贡献程度等情况，还用不同的颜色区分了不同层次的组织和人员的分布状态。

这些都是数据查询处理和简单的数据分析难以做到的。

作业清单（4/22）

【1】 继续安装Python 3.X 和 Orange3 软件，是否完成？

已完成

【2】 完成常用的概率分布代码，如下图

• 正态分布(Nomal Distribution)

import numpy as np
import matplotlib.pyplot as plt
import math
# 均值
u = 0
#标准差 
sig = math.sqrt(0.2)

x = np.linspace(u - 3 * sig, u + 3 * sig, 50)
y_sig = np.exp(-(x - u) ** 2 / (2 * sig ** 2) / (math.sqrt(2 * math.pi) * sig))
plt.plot(x,y_sig,"r-",linewidth=2)
plt.grid(True)
plt.show()

正态分布概率密度函数曲线

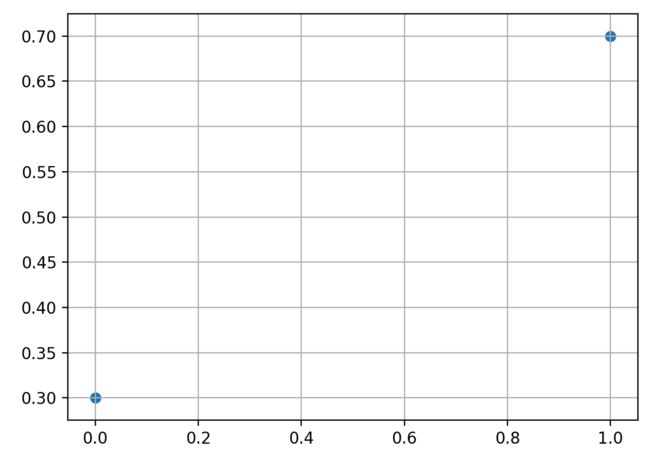
• 两点分布 /伯努利分布(Two Point Distribution)

import numpy as np
import matplotlib.pyplot as plt
p = 0.7
x = [0,1]
y = [1-p, p]
plt.scatter(x,y) # 散点图
plt.grid(True)
plt.show()

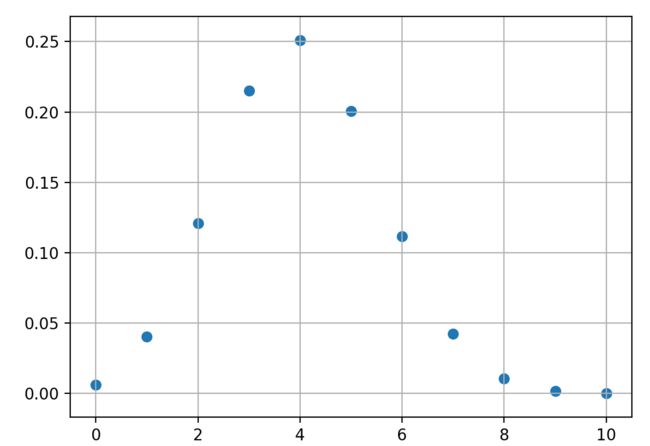
• 二项分布 (Binomial Distribution)

二项分布，即重复n次的伯努利试验，用ξ表示随机试验的结果。如果事件发生的概率是p,则不发生的概率q=1-p，N次独立重复试验中发生K次的概率是
P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!). 那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p)
期望：Eξ=np；
方差：Dξ=npq, 其中q=1-p

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
p = 0.4
n = 10
x = np.linspace(0,n,n+1)
y = comb(n,x)*p**x*(1-p)**(n-x)
print(x)
print(y)
plt.scatter(x,y)
plt.grid(True)
plt.show()

• 几何分布 (Geometric Distribution)

import numpy as np
import matplotlib.pyplot as plt
p = 0.4
n = 10
x = np.linspace(1,n,n)
y = p*(1-p)**(x-1)
print(x)
print(y)
plt.scatter(x,y)
plt.grid(True)
plt.show()

• 泊松分布（Possion Distribution)

import numpy as np
import matplotlib.pyplot as plt

x = np.random.poisson(lam = 5, size = 10000)
pillar = 15
a = plt.hist(x, pillar, color = 'g')
plt.plot(a[1][0:pillar], a[0],'r')
plt.grid()
plt.show()

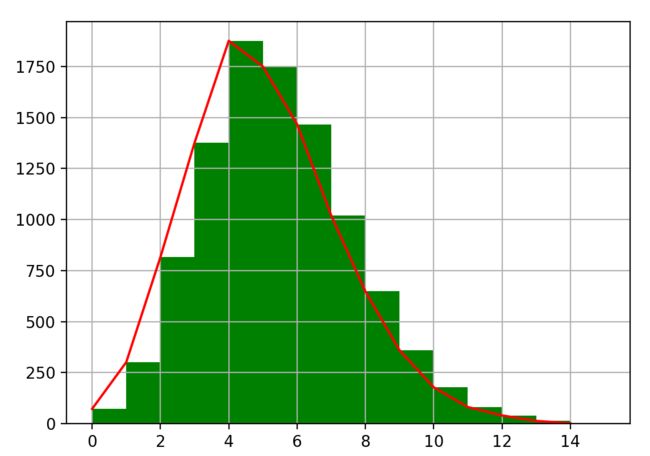
• 均匀分布 (Uniform Distribution)

import numpy as np
import matplotlib.pyplot as plt
a = 3
b = 5
x = np.linspace(a, b, 50)
y = []
for i in range(0,50):
	y.append(1 / (b - a))
plt.plot(x,y,"r-",linewidth=2)
plt.grid(True)
plt.show()

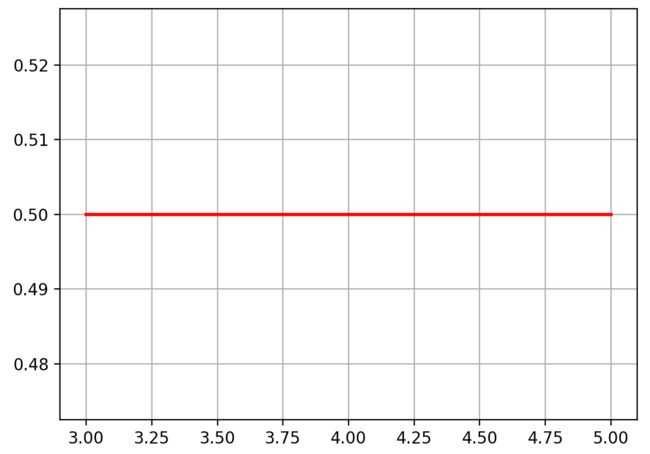
• 指数分布 (Exponential Distribution)

import numpy as np
import matplotlib.pyplot as plt

x = np.random.exponential(scale = 100, size = 10000)
pillar = 25
a = plt.hist(x, pillar, color = 'g')
plt.plot(a[1][0:pillar], a[0],'r')
plt.grid()
plt.show()

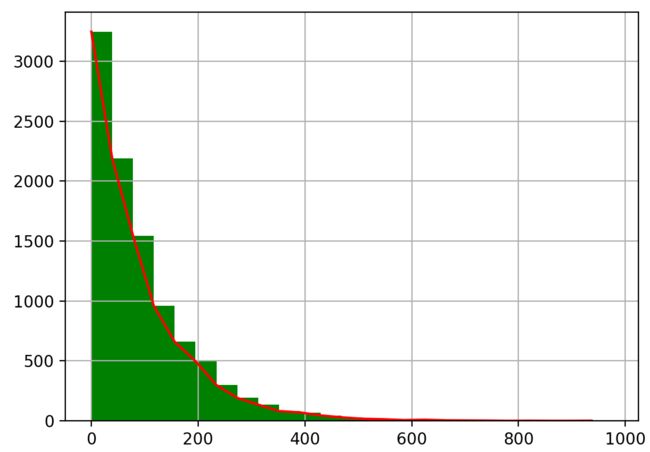
【3】 完成最大似然估计MLE的Python代码

用最大似然估计方法，估计正态分布的平均数，方差

import numpy as np

fig = plt.figure()
mu = 30  # mean of distribution
sigma = 2  # standard deviation of distribution
x = mu + sigma * np.random.randn(10000)

def mle(x):
    u = np.mean(x)
    return u, np.sqrt(np.dot(x - u, (x - u).T) / x.shape[0])

print(mle(x))

【4】 DM Lab2 实验结果用orange3挖掘（选做）

csv、线性回归

【1】 熟悉CSV文件的打开、读取和写入数据。

csv文件是一个文本文件，其中，列中的值由逗号分隔

• 将数据写入csv文件

利用pandas包将数据写入DataFrame，再将DataFrame存储为csv文件

import pandas as pd

# 多组列表
no = [1, 2, 3, 4, 5, 6, 7]
square_feet = [150, 200, 250, 300, 350, 400, 400]
price = [6450, 7450, 8450, 9450, 11450, 15450, 18450]

# 字典中的key值即为csv中的列名
data = pd.DataFrame({'No': no, 'square_feet': square_feet, 'price': price})

# 将DataFrame存储为csv, index 表示是否显示行名， default = True
data.to_csv("data/房价.csv", index=False, sep=',')

• 从csv文件中读取数据

pandas库提供read_csv

import pandas as pd
data = pd.read_csv('data/房价.csv')
print(data)

【2】 利用Orange3和Python orange方法完成线性回归

import Orange
import matplotlib.pyplot as plt
data = Orange.data.Table("F:\大三下\数据挖掘\DM_Lab\房价")
out_learner = Orange.regression.LinearRegressionLearner()

model = out_learner(data)

【3】 思考最大似然估计MLE和最小二乘之间的关系？

​ 最小二乘法以估计值与观测值的差的平方和作为损失函数，极大似然法则是以最大化目标值的似然概率函数为目标函数，从概率统计的角度处理线性回归并在似然概率函数为高斯函数的假设下同最小二乘建立了的联系。

【4】 根据DM Lab3数据散点图，画出一元回归线。

import numpy
from pandas import read_csv
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# 导入数据
data = read_csv('test1.csv')
u =data.corr() # 相关性系数
print(u)

lrModel = LinearRegression()
x = data.活动推广费.values.reshape(-1,1)
lrModel.fit(x,data.销售额)
print(lrModel.predict([[75]]))
alpha = lrModel.intercept_
beta = lrModel.coef_
new_r = alpha + beta * numpy.array([75])


plt.scatter(data.活动推广费,data.销售额)
plt.plot(data.活动推广费,lrModel.predict(x))
plt.show()

【5】 根据DM Lab3实验过程，母亲身高167cm，预测孩子身高可能是多少？

import numpy as np
from sklearn.linear_model import LinearRegression
x = [154,157,158,159,160,161,162,163]
y = [155,156,159,162,161,164,165,166]

model = LinearRegression()
x =np.array(x).reshape(-1,1)
print(x)
model.fit(x,y)
print(model.predict([[167]]))

预测孩子身高171.4 cm

作业清单（4/29、5/4）

【1】 根据下列数据集（数据表存为csv格式）建立线性回归模型。

(1) 预测面积为1000平方英尺的房子价格。

要求: 完成2遍，第1遍可以参考课堂笔记、查阅网络资料等方式完成；第2遍不参考任何辅助方式，限定15分钟内独立编写代码，完成此回归模型。

(2) 建立多元回顾模型。至少增加2项房子价格的特征，例如：地段、新旧等因素。

(3) 将（1）和（2）整理成实验报告。5月6日上课检查实验报告情况。

实验报告

1. 一元回归——通过面积预测房价

• 数据集：csv格式

No,square_feet,price
1,150,6450
2,200,7450
3,250,8450
4,300,9450
5,350,11450
6,400,15450
7,500,18450

• 从csv文件中读取数据

import pandas as pd
data = pd.read_csv('data/房价.csv')

• 建立线性回归模型

from sklearn.linear_model import LinearRegression

model = LinearRegression()
x = data['square_feet'].values.reshape(-1, 1)
y = data['price']
model.fit(x, y)

• 预测面积为 1000 平方英尺的房子价格

print(model.predict([[1000]]))

• 画图

import matplotlib.pyplot as plt
plt.scatter(data['square_feet'], y, color='blue')
plt.plot(x, model.predict(x), 'r-')
plt.grid(True)
plt.show()

• 实验结果
  • 预测面积为 1000 平方英尺的房子价格为35839.34
  • 从得到的图片可以直观看出，模型的拟合效果不错。

2. 建立多元回归模型——波士顿房价预测

数据集

下载链接

属性	含义	属性	含义
CRIM	城镇人均犯罪率	ZN	住宅用地超过 25000 sq.ft. 的比例。
INDUS	城镇非零售商用土地的比例	CHAS	查理斯河空变量（如果边界是河流，则为1；否则为0）
NOX	一氧化氮浓度	RM	住宅平均房间数
DIS	到波士顿五个中心区域的加权距离	RAD	辐射性公路的接近指数
TAX	每 10000 美元的全值财产税率	PTRATIO	城镇师生比例
B	1000（Bk-0.63）^ 2，其中 Bk 指代城镇中黑人的比例	LSTAT	人口中地位低下者的比例。
MEDV	自住房的平均房价，以千美元计

使用的第三方库

• pandas: csv文件读取、数据集整理
• sklearn.linear_model.LinearRegression: 线性回归模型
• sklearn.model_selection.train_test_split 数据集划分为训练集、测试集

import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

读取并处理数据

• 读取数据

data = pd.read_csv('data/housing.csv')

• 不考虑城镇人均犯罪率，模型评分较高

# 不要第一列的数据
new_data = data.iloc[:, 1:]

查看数据

• 查看处理后的数据集

# 得到数据集且查看
print('head:', new_data.head(), '\nShape:', new_data.shape)

• 检查是否存在缺失值

# 缺失值检验
print(new_data[new_data.isnull().sum())

查看数据分散情况——绘制箱形图

• 输出行数count，平均值mean，标准差std，最小值min，最大值max，上四分位数75%, 中位数50%，下四分位数25%

print(new_data.describe())

• 箱型图绘制代码

new_data.boxplot()
plt.show()

数据集分割

将原始数据按照2:8比例分割为“测试集”和“训练集”

X_train, X_test, Y_train, Y_test = train_test_split(new_data.iloc[:, :13], new_data.MEDV, train_size=.80)

建立多元回归模型

根据训练集建立模型

model = LinearRegression()
model.fit(X_train, Y_train)
a = model.intercept_
b = model.coef_
print("最佳拟合线:截距", a, ",回归系数：", b)

score = model.score(X_test, Y_test)
print(score)

原始数据特征: (506, 13) ,训练数据特征: (404, 13) ,测试数据特征: (102, 13)
原始数据标签: (506,) ,训练数据标签: (404,) ,测试数据标签: (102,)
最佳拟合线:截距 0.0 ,回归系数： [-1.74325842e-16  1.11629233e-16 -1.79794258e-15  7.04652389e-15
 -2.92277767e-15  2.97853711e-17 -8.23334194e-16  1.17159575e-16
  1.88696229e-17 -3.41643920e-16 -1.28401929e-17 -5.78208730e-17
  1.00000000e+00]
1.0

测试

Y_pred = model.predict(X_test)
print(Y_pred)
plt.plot(range(len(Y_pred)), Y_pred, 'b', label="predict")
plt.show()

画图表示结果

分别画出实际值和预测值的折线

X_train, X_test, Y_train, Y_test = train_test_split(new_data.iloc[:, :13], new_data.MEDV, train_size=.80)

plt.figure()
plt.plot(range(len(X_test)), Y_pred, 'b', label="predict")
plt.plot(range(len(X_test)), Y_test, 'r', label="test")
plt.legend(loc="upper right")
plt.xlabel("the number of MEDV")
plt.ylabel('value of MEDV')
plt.show()

实验结果分析

• 根据预测值画出的折线和根据实际值画出的折线走向大致吻合，可以看出训练的模型效果挺好的，用sklearn的score得到1.0的评分，也可以印证这一点。

知识点总结

• 回归分析

  回归分析的目的是考察变量之间的数量关系，主要解决以下几个问题：

  （1）利用一组样本数据，确定变量之间的数学关系式；

  （2）对这些关系式的可信程度进行各种统计检验，找出哪些变量的影响是显著的，哪些是不显著的；

  （3）利用关系式，根据一个或几个变量的取值来估计另一个变量的取值，并给出估计的可靠程度。

• 一元线性回归

  只涉及一个自变量的回归称为一元回归，描述两个具有线性关系的变量之间关系的方程称为回归模型，一元线性回归模型可表示为：
  $$y=ax+b$$

  上式称为理论回归模型，对它有以下假定：

  （1）y与x之间具有线性关系；

  （2）x是非随机的，在重复抽样中，x的取值是固定的。一元线性回归的估计的回归方程形式为：

• 多元回归分析

  用回归方程定量地刻画一个因变量与多个自变量间的线性依存关系,称为多元回归分析,简称多元回归。

  

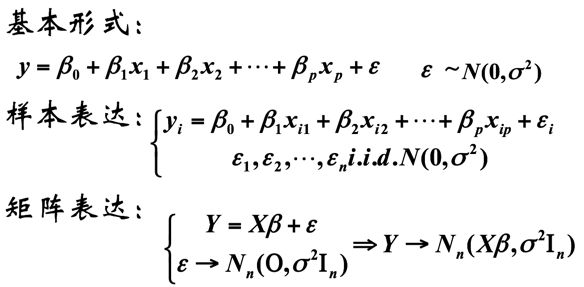
• DataFrame.iloc常见用法

  得到属性名、第一行数据、数据类型

  print(data.iloc[0])
  

  No                1
  square_feet     150
  loaction          4
  built            10
  price          6450
  Name: 0, dtype: int64
  

  得到属性名、第二行数据、数据类型

  print(data.iloc[1])
  

  No                2
  square_feet     200
  loaction          5
  built             9
  price          7450
  Name: 1, dtype: int64
  

  得到全部数据

  方法一

  print(data.iloc[:])
  

  方法二

  print(data.iloc[0:])
  

  方法三

  print(data.iloc[:, :])
  

     No  square_feet  loaction  built  price
  0   1          150         4     10   6450
  1   2          200         5      9   7450
  2   3          250         3      7   8450
  3   4          300         3      4   9450
  4   5          350         4      3  11450
  5   6          400         2      4  15450
  6   7          400         1      2  18450
  

  得到第二行开始的数据

  print(data.iloc[1:])
  

     No  square_feet  loaction  built  price
  1   2          200         5      9   7450
  2   3          250         3      7   8450
  3   4          300         3      4   9450
  4   5          350         4      3  11450
  5   6          400         2      4  15450
  6   7          400         1      2  18450
  

  得到第3-n行，第4-m列的数据（假设共有n行，m列）

  print(data.iloc[2:, 3:])
  

     built  price
  2      7   8450
  3      4   9450
  4      3  11450
  5      4  15450
  6      2  18450
  

• 箱形图（Box-plot）是一种用作显示一组数据分散情况资料的统计图。

• 箱线图的绘制方法是：先找出一组数据的上边缘、下边缘、中位数和两个四分位数；然后， 连接两个四分位数画出箱体；再将上边缘和下边缘与箱体相连接，中位数在箱体中间。
  

过拟合&欠拟合

【2】 结合下图(a)和(b)解释什么是过拟合和欠拟合？通常用什么方法解决这两个问题？

• 过拟合

  过拟合是指学习时选择的模型所包含的参数过多，以至于出现这一模型对已知数据预测得很好，对未知数据预测的很差的现象。

• 过拟合出现原因

  • 建模样本选取有误，如样本数量太少，选样方法错误，样本标签错误等，导致选取的样本数据不足以代表预定的分类规则
  • 样本噪音干扰过大，使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
  • 假设的模型无法合理存在，或者说是假设成立的条件实际并不成立
  • 参数太多，模型复杂度过高
  • 对于决策树模型，如果我们对于其生长没有合理的限制，其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event)，使其虽然可以完美匹配（拟合）训练数据，但是无法适应其他数据集
  • 对于神经网络模型：
    对样本数据可能存在分类决策面不唯一，随着学习的进行,，BP算法使权值可能收敛过于复杂的决策面；
    b)权值学习迭代次数足够多(Overtraining)，拟合了训练数据中的噪声和训练样例中没有代表性的特征

• 过拟合解决方法

  1. 正则化方法

     正则化方法是指在进行目标函数或代价函数优化时，在目标函数或代价函数后面加上一个正则项，一般有L1正则与L2正则等。

     • L1正则：
       

       L1正则即在原有的损失函数的基础上添加参数向量的L1范数，正则项的系数用于平衡原有损失函数和正则项之间的关系。

     • L2正则
       

       L2正则即在原有的损失函数的基础上添加参数向量的L2范数。

       在损失函数中添加正则项符合奥斯卡姆剃刀原理：在所有可能选择的模型中，能够很好解释已知数据并且十分简单的模型才是最好的模型。

  2. 交叉验证

     如果给定的样本数据充足，进行模型选择的一种简单方法是随机地将数据集切分为三部分，分别为训练集，验证集和测试集。

     训练集用来训练模型，验证集用于模型的选择，测试集用于方法的评估。

     在学习到不同复杂度的模型中，选择对验证集有最小预测误差的模型。

     交叉验证有以下几种方法：

     1、简单交叉验证
     随机地将已给数据分为两部分，一部分作为训练集，一部分作为测试集，然后用训练集在各种条件下训练模型，从而得到不同的模型，在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

     2、S折交叉验证
     首先随机地将已给数据切分为S个互不相交的大小相同的子集，然后利用S-1个子集的数据训练模型，利用余下的子集测试模型，将这一过程对可能的S种选择重复进行，最后选出S次评测中平均测试误差最小的模型。

     3、留一交叉验证
     S折交叉验证的一种特殊情况，即S=N（N为训练集样本的数量）

  3. Early stopping

     对模型进行训练的过程即是对模型的参数进行学习更新的过程，这个参数学习的过程往往会用到一些迭代方法，如梯度下降（Gradient descent）学习算法。

     Early stopping便是一种迭代次数（epochs）截断的方法来防止过拟合，即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。

     具体做法是，在每一词迭代结束时（一个迭代集为对所有的训练数据的一轮遍历）计算验证集的accuracy，当accuracy不再提高时，就停止训练。

     在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次迭代（或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了。这种策略也称为“No-improvement-in-n”，n即迭代的次数，可以根据实际情况取，如10、20、30……

  4. 数据集扩充

     在数据挖掘领域流行着这样的一句话，“有时候往往拥有更多的数据胜过一个好的模型”。

     训练数据与将来的数据是独立同分布的
       
     一般有以下方法：

  • 从数据源采集更多数据
  • 复制原有数据并加上随机噪声
  • 重采样
  • 根据当前数据集估计数据分布参数，使用该分布产生更多数据等

  5. Dropout

     Dropout方法是通过修改ANN中隐藏层的神经元个数来防止ANN的过拟合。

• 欠拟合

  “欠拟合”常常在模型学习能力较弱，而数据复杂度较高的情况出现，此时模型由于学习能力不足，无法学习到数据集中的“一般规律”，因而导致泛化能力弱。

• 欠拟合出现原因

  • 模型复杂度过低
  • 特征量过少

• 常见解决方法

  • 增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间
  • 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强
  • 减少正则化参数，正则化的目的是用来防止过拟合的，但是模型出现了欠拟合，则需要减少正则化参数
  • 使用非线性模型，比如核SVM 、决策树、深度学习等模型
  • 调整模型的容量(capacity)，通俗地，模型的容量是指其拟合各种函数的能力
  • 容量低的模型可能很难拟合训练集；使用集成学习方法，如Bagging ,将多个弱学习器Bagging

• 参考文章

  过拟合
  欠拟合和过拟合出现原因及解决方案

【3】 预测鲍鱼的年龄。网上下载“鲍鱼数据集”（见微信群，鲍鱼数据集.csv），建立线性回归模型，指出简单线性回归模型进行预测的问题，思考如何解决？

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 读取鲍鱼数据集（数据集下载链接：https://aistudio.baidu.com/aistudio/datasetdetail/361）
data = pd.read_csv('鲍鱼年龄.csv')
# 清理数据
new_data = data.iloc[:, 1:]
# 得到数据集且查看
print('head:', new_data.head(), '\nShape:', new_data.shape)

print(new_data.describe())
# 缺失值检验
print(new_data[new_data.isnull() == True].count())
new_data.boxplot()
plt.show()
print(data.corr())
print(new_data.corr())
X_train, X_test, Y_train, Y_test = train_test_split(new_data.iloc[:, :8], new_data.年龄, train_size=.80)
print("原始数据特征:", new_data.iloc[:, :8].shape, ",训练数据特征:", X_train.shape, ",测试数据特征:", X_test.shape)
print("原始数据标签:", new_data.年龄.shape, ",训练数据标签:", Y_train.shape, ",测试数据标签:", Y_test.shape)

model = LinearRegression()
model.fit(X_train, Y_train)
a = model.intercept_
b = model.coef_
print("最佳拟合线:截距", a, ",回归系数：", b)
# 模型评分
score = model.score(X_test, Y_test)
print(score)

Y_pred = model.predict(X_test)
print(Y_pred)
plt.plot(range(len(Y_pred)), Y_pred, 'b', label="predict")
plt.show()

X_train, X_test, Y_train, Y_test = train_test_split(new_data.iloc[:, :8], new_data.年龄, train_size=.80)

plt.figure()
plt.plot(range(len(Y_pred)), Y_pred, 'b', label="predict")
plt.plot(range(len(X_test)), Y_test, 'r', label="test")
plt.legend(loc="upper right")
plt.xlabel("the number of age")
plt.ylabel('value of age')
plt.show()

• 问题

  （1）线性回归在数据量较少的情况下会出现过拟合的现象

  （2）对于非线性数据或者数据特征间具有相关性多项式回归难以建模.

  （3）难以很好地表达高度复杂的数据。

• 解决

  • 使用ridge、Lasso回归可以在一定程度上解决过拟合问题。

【4】 Python实现新型冠状病毒传播模型及预测（选做）

数据清洗

【1】 数据清洗是数据挖掘模型建立过程中很重要的一步吗一般，清洗的方法包括什么？

• 数据清洗是数据挖掘模型建立过程中很重要的一步。 数据清洗是指发现并纠正数据文件中可识别的错误的最后一道程序，包括检查数据一致性，处理无效值和缺失值等。

• 数据清洗的方法:

  数据清理一般针对具体应用，因而难以归纳统一的方法和步骤，但是根据数据不同可以给出相应的数据清理方法。

  1.解决不完整数据（ 即值缺失）的方法

  大多数情况下，缺失的值必须手工填入（ 即手工清理）。当然，某些缺失值可以从本数据源或其它数据源推导出来，这就可以用平均值、最大值、最小值或更为复杂的概率估计代替缺失的值，从而达到清理的目的。

  2.错误值的检测及解决方法

  用统计分析的方法识别可能的错误值或异常值，如偏差分析、识别不遵守分布或回归方程的值，也可以用简单规则库（ 常识性规则、业务特定规则等）检查数据值，或使用不同属性间的约束、外部的数据来检测和清理数据。

  3.重复记录的检测及消除方法

  数据库中属性值相同的记录被认为是重复记录，通过判断记录间的属性值是否相等来检测记录是否相等，相等的记录合并为一条记录（即合并/清除)。合并/清除是消重的基本方法。

  4.不一致性（ 数据源内部及数据源之间）的检测及解决方法

  从多数据源集成的数据可能有语义冲突，可定义完整性约束用于检测不一致性，也可通过分析数据发现联系，从而使得数据保持一致。

---

【2】 采用删除和填补两种方法进行清洗数据。

import pandas as pd
import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

data = pd.read_csv('Iris.csv')

data1 = data.dropna() # 删除数据缺失的行
data2 = data.dropna(axis=1)# 删除数据缺失的列

print(data.fillna(method='pad'))# 同一列上一行的数填补
print(data.fillna(0)
print(data.fillna(data.mean()))# 同一列平均值填补
print(data.fillna(data.median()))# 同一列中位数填补
print(data.fillna(data.mode()))# 同一列众数填补

【3】 对【2】题数据采用回归方法填补。

import pandas as pd
import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

data = pd.read_csv('Iris.csv')

new_data = data.iloc[:, 0:4]

model = IterativeImputer(max_iter=10, random_state=0)
model.fit(new_data)

print(model.transform(new_data))

作业清单（5/11）

【1】 Pandas Series是什么? Pandas中的DataFrame是什么？如何将numpy数据转成DataFrame格式的数据？如何将Series数据转成DataFrame格式的数据？如何将DataFrame转换为NumPy数组？如何对DataFrame进行排序？什么是数据聚合？（注：每一小问，举例说明）

Pandas是什么？

Pandas是一个强大的分析结构化数据的工具集；它的使用基础是Numpy（提供高性能的矩阵运算）；用于数据挖掘和数据分析，同时也提供数据清洗功能。

• 导入

import pandas as pd

• Pandas排序方式
  • 根据索引排序sort_index()
  • 根据实际值排序sort_values()排序
  • 默认升序，参数ascending=False时为降序

【一维数据：Pandas Series】

它是一种类似于一维数组的对象，是由一组数据(各种NumPy数据类型)以及一组与之相关的数据标签(即索引)组成。仅由一组数据也可产生简单的Series对象。

>>> import pandas as pd
>>> import numpy as np
>>> b = pd.Series(np.arange(5))
>>> b
0    0
1    1
2    2
3    3
4    4
dtype: int32
>>> s = pd.Series(np.arange(5),index=['a','b','c','d','e'])
>>> print(s)
a    0
b    1
c    2
d    3
e    4
dtype: int32

• 通过字典创建Series对象

>>> dict={'apple':45,'orange':23,'peach':12}
>>> s =Series(dict)
>>> s = pd.Series(dict)
>>> s
apple     45
orange    23
peach     12
dtype: int64

• 取值

>>> a = pd.Series([1,2,3])
>>> a.values
array([1, 2, 3], dtype=int64)
>>> print(a.values)
[1 2 3]

• 根据索引取值

>>> a[2]
3

• 根据索引进行排序（升序）

>>> s = pd.Series([56,34,45,67,12,67,84],index = list('gbcadfe'))
>>> s.sort_index()
a    67
b    34
c    45
d    12
e    84
f    67
g    56
dtype: int64

• 根据值进行排序（升序）

>>> s.sort_values()
d    12
b    34
c    45
g    56
a    67
f    67
e    84
dtype: int64

【二维数据：DataFrame】

DataFrame是Pandas中的一个表格型的数据结构，包含有一组有序的列，每列可以是不同的值类型(数值、字符串、布尔型等)，DataFrame即有行索引也有列索引，可以被看做是由Series组成的字典。

• 创建

import pandas as pd

a = [[1,2,3],
	[4,5,6],
	[7,8,9]]
df = pd.DataFrame(a,index=list('123'),columns = ['A', 'B', 'C'])
print(df)

​ 运行结果

   A  B  C
1  1  2  3
2  4  5  6
3  7  8  9

• 将numpy数据转成DataFrame格式的数据

>>> import pandas as pd
>>> import numpy as np
>>> c = np.arange(20,32).reshape(3,4)
>>> c
array([[20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])
>>> c = pd.DataFrame(c)
>>> c
    0   1   2   3
0  20  21  22  23
1  24  25  26  27
2  28  29  30  31
>>> c = pd.DataFrame(c,index=list('abc'),columns=list('ABCD'))
>>> c
    A   B   C   D
a NaN NaN NaN NaN
b NaN NaN NaN NaN
c NaN NaN NaN NaN
>>> d = np.arange(20,32).reshape(3,4)
>>> c = pd.DataFrame(d,index=list('abc'),columns=list('ABCD'))
>>> c
    A   B   C   D
a  20  21  22  23
b  24  25  26  27
c  28  29  30  31

• 将DataFrame转换为NumPy

>>> a = [[4,6,1],[3,5,2],[9,5,7]]
>>> df = pd.DataFrame(a,index=list('cbd'),columns=list('ahg'))
>>> df.values
array([[4, 6, 1],
       [3, 5, 2],
       [9, 5, 7]], dtype=int64)

• 将Series数据转成DataFrame格式的数据

>>> import pandas as pd
>>> import numpy as np
>>> s = pd.Series(np.arange(5),index = list('abcde'))
>>> s
a    0
b    1
c    2
d    3
e    4
dtype: int32
>>> s = pd.DataFrame(s)
>>> s
   0
a  0
b  1
c  2
d  3
e  4   

• 数组对DataFrame进行排序
  • 根据索引排序

>>> a = [[4,6,1],[3,5,2],[9,5,7]]
>>> df = pd.DataFrame(a,index=list('cbd'),columns=list('ahg'))
>>> df.sort_index() # 根据行索引排列
   a  h  g
b  3  5  2
c  4  6  1
d  9  5  7
>>> df.sort_index(ascending=False) # 根据行索引降序排列
   a  h  g
d  9  5  7
c  4  6  1
b  3  5  2
>>> df.sort_index(axis=1) # 根据列索引排列
   a  g  h
c  4  1  6
b  3  2  5
d  9  7  5
>>> df.sort_index(axis=1,ascending=False) # 根据列索引排列
   h  g  a
c  6  1  4
b  5  2  3
d  5  7  9

​ - 根据实际值排序

​ 通过by参数指定需要排序的列值，可指定多列

>>> df.sort_values(by='h') # 根据h列的值升序排列
   a  h  g
b  3  5  2
d  9  5  7
c  4  6  1
>>> df.sort_values(by='h',ascending=False)# 根据h列的值降序排列
   a  h  g
c  4  6  1
b  3  5  2
d  9  5  7
>>> df.sort_values(by=['h','g'],ascending=False)# 优先考虑排在前面的列
   a  h  g
c  4  6  1
d  9  5  7
b  3  5  2

---

【2】 利用iris.csv数据集，建立KNN模型，预测Sepal.Length\Sepal.Width\Petal.Length\Petal.Width分别为(6.3，3.1，4.8，1.4)时，属于鸢尾花的哪个类别？编写KNN源代码。

KNN(K-NearestNeighbor) 算法思想:

令D为训练数据集，当测试集d出现时，将d与D中所有的样本进行比较，计算他们之间的相似度（或者距离）。从D中选出前k个最相似的样本，则d的类别由k个最近邻的样本中出现最多的类别决定。

from numpy import *
import pandas as pd

data = pd.read_csv('Iris.csv')
dataSet = data.iloc[:, 0:4]
labels = data['Species']
print(labels)
# 行数
numSamples = dataSet.shape[0]
print(numSamples)

# 测试数据 Iris-versicolor
new_t = array([6.3, 3.1, 4.8, 1.4])

# 求欧式距离
diff = tile(new_t, (numSamples, 1))-dataSet
squreDiff = diff**2
squreDist = sum(squreDiff, axis=1)
distance = squreDist ** 0.5
print(distance)

# 从小到大排序
sortedDistIndices = argsort(distance)

print(sortedDistIndices)
classCount = {}
K = 4
for i in range(K):
    voteLabel = labels[sortedDistIndices[i]]
    print(voteLabel)
    classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
print(classCount)

maxCount = 0
for k, v in classCount.items():
    if v > maxCount:
        maxCount = v
        maxIndex = k

print("Your input is:", new_t, "and classified to class: ", maxIndex)

• 预测Sepal.Length\Sepal.Width\Petal.Length\Petal.Width分别为(6.3，3.1，4.8，1.4)时，属于鸢尾花setosa.

【3】 计算X = [1,2,3]和Y = [0,1,2]的曼哈顿距离(Manhattan Distance)，切比雪夫距离 ，闵可夫斯基距离，标准化欧氏距离，马氏距离。给出计算公式，并根据公式计算。利用Python实现上述距离。

【曼哈顿距离(Manhattan Distance)】

• 公式：

$$d(x,y)=\sum _{k=1}^n|x_k-y_k|$$

• python 代码

  def ManhattanDist(A,B):
  	return sum([abs(a-b) for (a,b) in zip(A,B)])
  

【切比雪夫距离 （ Chebyshev distance ）】

• 公式

$$d(x,y)=max(|x_k-y_k|)$$

​ 其中k = 1,2,3,…,n

• python代码

  # 切比雪夫距离
  def cheDist(A, B):
  	return max([abs(a - b) for (a, b) in zip(A, B)])
  

【闵可夫斯基距离( Minkowski distance )】

• 公式

$$d(x,y)=(\sum _{k=1}^n|x_k-y_k{|}^p{)}^{1/p}$$

​ p = 1: 曼哈顿距离

​ p = 2: 欧式距离

• python代码

  # 闵可夫斯基距离
  def minkowskiDist(A, B, p):
  	return sum([abs(a - b)**p for (a, b) in zip(A,B)])**(1/p)
  

【欧氏距离】

• 公式：
  $$d(x,y)=\sqrt{\sum _{k=1}^n(x_k-y_k{)}^2}$$

• python 代码

  import math
  def eculiDist(A,B):
      return math.sqrt(sum([(a - b)**2i for (a.b) in zip(A,B)]))
  

【标准化欧氏距离】

• 公式
  $$d(x,y)=\sqrt{\sum _{k=1}^n(\frac{x_k-y_k}{s_k}{)}^2}，s_k为各分量的方差$$

  def standardEucliDist(A,B):
  	X=np.vstack([A,B])
  	sk=np.var(X,axis=0,ddof=1)
  	#print(sk)
  	return np.sqrt(sum([((x - y) ** 2 /sk) for (x,y) in zip(A,B)]))
  

【马氏距离】

• 公式

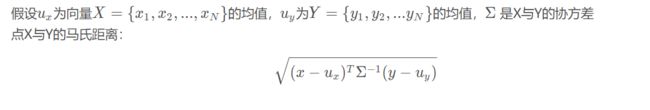
如果Σ是单位矩阵，则马氏距离退化成欧式距离；
如果Σ是对角矩阵，则称为归一化后的欧式距离。

def mashi_distance(x,y):
    X=np.vstack([x,y])
    print(X)
    XT=X.T
    print(XT)


    S=np.cov(X)   #两个维度之间协方差矩阵
    SI = np.linalg.inv(S) #协方差矩阵的逆矩阵
    #马氏距离计算两个样本之间的距离，此处共有4个样本，两两组合，共有6个距离。
    n=XT.shape[0]
    d1=[]
    for i in range(0,n):
        for j in range(i+1,n):
            delta=XT[i]-XT[j]
            d=np.sqrt(np.dot(np.dot(delta,SI),delta.T))
            print(d)
            d1.append(d)

作业清单（5/13）

【1】选择4名同学A、B、C、D，两次小测成绩，利用Kmeans算法分为“优秀”和“及格”两类。@注意：不能直接调用sklearn第三方库的KMeans函数，根据课堂讲授的分类过程，编写代码。撰写实验报告。

学生姓名	小测1	小测2
A	1	1
B	2	1
C	4	3
D	5	4

KMeans实验报告（K=2）

实验目的

• 选择4名同学A、B、C、D，两次小测成绩，利用Kmeans算法分为“优秀”和“及格”两类。

• 限制：不能直接调用sklearn第三方库的KMeans函数。

学生姓名	小测1	小测2
A	1	1
B	2	1
C	4	3
D	5	4

实验步骤

1. 数据准备

• 将数据储存为字典对象

  data = {'A': [1, 1], 'B': [2, 1], 'C': [4, 3], 'D': [5, 4]}
  

• 为了方便取值，将数据进一步转化成Series对象

  import pandas as pd
  
  # 转成Series, 方便取值
  data = pd.Series(data)
  
  # print(data.values[1])
  # print(data.index[2])
  

2. KMeans算法实现

• KMeans算法涉及两点之间距离的计算，我们提前写好一个函数：输入两个点的坐标，返回两点之间的欧氏距离

• def eucliDist(A, B):
      return math.sqrt(sum([(a - b) ** 2 for (a, b) in zip(A, B)]))
  

• 函数k_means(c,data)实现KMeans算法：

  a. 输入质心列表c，待聚类Series对象data

  b. 计算data中的每个点分到2个质心的距离，得到一个矩阵，如

  [[0.0, 1.0, 3.605551275463989, 5.0], [1.0, 0.0, 2.8284271247461903, 4.242640687119285]]
  

  c. 比较矩阵同一列的数值大小，将对应的学生划归距离较短的质心所属的类，将标签存储为列表，如

  ['及格', '优秀', '优秀', '优秀']
  

  d. 重新计算质心的坐标，新质心的坐标=被划归同一类点的坐标的平均值

  e. 重复b~d，直到质心坐标不再变化

  f. 返回标签列表

  • 完整函数如下

  def k_means(c,data):
      # a. 输入质心列表`c`，待聚类Series对象`data`
  
      # b. 计算data中的每个点分到2个质心的距离，得到一个矩阵，如
      metrix = [[eucliDist(a, b) for a in data.values] for b in c]
      print(metrix)
      # c. 比较矩阵同一列的数值大小，将对应的学生划归距离较短的质心所属的类，将标签存储为列表
      classifier = ['及格' if a < b  else '优秀' for(a,b) in zip(metrix[0],metrix[1]) ]
      print(classifier)
  
      # d. 重新计算质心的坐标，新质心的坐标=被划归同一类点的坐标的平均值
      n1 = 0
      c1,c2 = [0, 0], [0, 0]
      num = len(data)
      for i in range(0, num):
  
          if classifier[i] == '及格':
              c1 = [a + b for (a,b) in zip(c1,data.values[i])]
              n1 = n1 + 1
          elif classifier[i] == '优秀':
              c2 = [a + b for (a,b) in zip(c2,data.values[i])]
  
      c1 = [a /n1 for a in c1]
      c2 = [a/(num - n1) for a in c2]
  
      # e. 重复b~d，直到质心坐标不再变化
      if c != [c1, c2]:
          c = [c1,c2]
          print("center:" + str(c))
          k_means(c, data)
      return classifier
  

3. 设置参数，调用函数，得到实验结果

• 因为要把数据分成两类，所以我们要选取K=2个点作为初始质心，分别为（1，1），（2，1）

  • 选取不同的初始质心，聚类结果不同

  # 选择K=2个点作为初始质心
  c = [[1,1], [2,1]]
  

• 调用函数

  label = k_means(c, data)
  

• 整理结果：以Series格式输出

  print(pd.Series((label), index = data.index))
  

实验结果

• 初始质点取[1,1], [2,1]时，结果为

学生姓名	小测1	小测2
A	1	1	及格
B	2	1	优秀
C	4	3	优秀
D	5	4	优秀

---

【2】根据下列成绩单，将5名同学成绩归为A类、B类、C类，利用Kmeans算法实现。@注意：不能直接调用sklearn第三方库的KMeans函数，根据课堂讲授的分类过程，编写代码。撰写实验报告。

学生姓名	小测1	小测2	小测3	期末成绩	项目答辩	成绩
张三	12	15	13	28	24	？
李四	7	11	10	19	21	？
王五	12	14	11	27	23	？
赵六	6	7	4	13	20	？
刘七	13	14	13	27	25	？

KMeans实验报告（K=3）

实验目的

• 根据下列成绩单，将5名同学成绩归为A类、B类、C类。

• 限制：使用Kmeans算法实现，但不直接调用sklearn第三方库的KMeans函数。

学生姓名	小测1	小测2	小测3	期末成绩	项目答辩	成绩
张三	12	15	13	28	24	？
李四	7	11	10	19	21	？
王五	12	14	11	27	23	？
赵六	6	7	4	13	20	？
刘七	13	14	13	27	25	？

实验步骤

1. 数据准备

• 将数据储存为csv文件，格式如下

  学生姓名,小测1,小测2,小测3,期末成绩,项目答辩
  张三,12,15,13,28,24
  李四,7,11,10,19,21
  王五,12,14,11,27,23
  赵六,6,7,4,13,20
  刘七,13,14,13,27,25
  

• 在从csv文件中读取数据，并选取可用的数据（排除姓名列）

  data = pd.read_csv('grade.csv')
  new_data = data.iloc[:, 1:].values
  

2. KMeans算法实现

• KMeans算法涉及两点之间距离的计算，我们提前写好一个函数：输入两个点的坐标，返回两点之间的欧氏距离

  def eucliDist(A, B):
      return math.sqrt(sum([(a - b) ** 2 for (a, b) in zip(A, B)]))
  

• 函数k_means(c,data,max,label)实现KMeans算法：

  a. 输入：质心列表c，待聚类数据data，最大迭代次数max，标签列表label

  b. 计算data中的每个点分别到3个质心的欧式距离，得到一个矩阵metrix

  metrix = [[eucliDist(a, b) for a in data] for b in c]
  

  c. 比较矩阵metrix同一列的数值大小，将对应的学生划归距离较短的质心所属的类，将标签存储为列表.

  classifier = []
      for (d, e, f) in zip(metrix[0], metrix[1], metrix[2]):
          m = min(d, e, f)
          if d == m:
              classifier.append(label[0])
          elif e == m:
              classifier.append(label[1])
          else:
              classifier.append(label[2])
  

  d. 重新计算质心的坐标，新质心的坐标=被划归同一类点的坐标的平均值

  n1, n2 = 0, 0
  c1 = [0, 0, 0, 0, 0]
  c2 = c1
  c3 = c1
      for i in range(0, num):
  
          if classifier[i] == label[0]:
              c1 = [a + b for (a, b) in zip(c1, data[i])]
              n1 = n1 + 1
          elif classifier[i] == label[1]:
              c2 = [a + b for (a, b) in zip(c2, data[i])]
              n2 = n2 + 1
          else:
              c3 = [a + b for (a, b) in zip(c3, data[i])]
  
      c1 = [a / n1 for a in c1]
      c2 = [a / n2 for a in c2]
      c3 = [a / (num - n1 - n2) for a in c3]
  

  e. 重复b~d，直到质心坐标不再变化或达到最大迭代次数

  f. 返回标签列表

  • 完整函数如下

  def k_means(c, data, max,label):
      # a. 输入质心列表c，待聚类数据`data`，最大迭代次数max
      max = max - 1
      num = len(data)
      # b. 计算data中的每个点分到k个质心的距离，得到一个矩阵，如
      metrix = [[eucliDist(a, b) for a in data] for b in c]
      print(metrix)
      # c. 比较矩阵同一列的数值大小，将对应的学生划归距离较短的质心所属的类，将标签存储为列表
      classifier = []
      for (d, e, f) in zip(metrix[0], metrix[1], metrix[2]):
          m = min(d, e, f)
          if d == m:
              classifier.append(label[0])
          elif e == m:
              classifier.append(label[1])
          else:
              classifier.append(label[2])
  
      print(classifier)
  
      # d. 重新计算质心的坐标，新质心的坐标=被划归同一类点的坐标的平均值
      n1, n2 = 0, 0
      c1 = [0, 0, 0, 0, 0]
      c2 = c1
      c3 = c1
      for i in range(0, num):
  
          if classifier[i] == label[0]:
              c1 = [a + b for (a, b) in zip(c1, data[i])]
              n1 = n1 + 1
          elif classifier[i] == label[1]:
              c2 = [a + b for (a, b) in zip(c2, data[i])]
              n2 = n2 + 1
          else:
              c3 = [a + b for (a, b) in zip(c3, data[i])]
  
      c1 = [a / n1 for a in c1]
      c2 = [a / n2 for a in c2]
      c3 = [a / (num - n1 - n2) for a in c3]
  
      print(max)
      print([c1,c2,c3])
      # e. 重复b~d，直到质心坐标不再变化,或达到最大迭代次数
      if c != [c1, c2, c3] and max > 0:
  
          c = [c1, c2, c3]
          print(c)
          k_means(c, data, max, label)
      return classifier
  

3. 设置参数，调用函数，得到结果

• 设置初始质心、标签列表、最大迭代次数

  # 选择K个点作为初始质心
  c = [[12, 15, 13, 28, 24], [ 7, 11, 10, 19, 21],[12, 14, 11, 27, 23]]
  label = ['A', 'B', 'C']
  max = 20
  

• 调用函数，整理结果

  grade = k_means(c, new_data, max, label)
  grade = pd.Series(grade, index=data['学生姓名'])
  print(grade)
  

实验结果

• 初始质心为[12, 15, 13, 28, 24], [ 7, 11, 10, 19, 21],[12, 14, 11, 27, 23]时，迭代2次即收敛，结果如下

学生姓名	小测1	小测2	小测3	期末成绩	项目答辩	成绩
张三	12	15	13	28	24	A
李四	7	11	10	19	21	B
王五	12	14	11	27	23	C
赵六	6	7	4	13	20	B
刘七	13	14	13	27	25	A

---

【3】 利用Sklearn的标准KNN和KMeans方法，数据集为“wine.csv”（见微信群），通过KNN算法，对葡萄酒的测试集进行标注，然后对比预测标签值和已知标签值，得到KNN算法的预测准确率。通过Kmeans算法，对无标签的“wine.csv”进行分类，自己设定K值和初始中心点值。

Sklearn的标准KNN类

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
import pandas as pd

data = pd.read_csv('wine.csv')

x_train,x_test,y_train,y_test = train_test_split(data.iloc[:, 0:13], data.iloc[:, 13])

# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

estimator = KNeighborsClassifier()
estimator.fit(x_train, y_train)
predict = estimator.predict(x_test)
score = estimator.score(x_test,y_test)
print(score)

• 预测准确率：0.9333333333333333

Sklearn的标准K-means类

KMeans类主要参数

• KMeans类的主要参数有：

参数	描述
n_clusters	k值，类别数
max_iter	最大迭代次数 （一般如果是凸数据集的话可以不管这个值，如果数据集不是凸的，可能很难收敛，此时可以指定最大的迭代次数让算法可以及时退出循环。）
n_init	用不同的初始化质心运行算法的次数。 （由于K-Means是结果受初始值影响的局部最优的迭代算法，因此需要多跑几次以选择一个较好的聚类效果，默认是10，一般不需要改。如果你的k值较大，则可以适当增大这个值。）
init	初始值选择的方式 (可以为完全随机选择’random’,优化过的’k-means++‘或者自己指定初始化的k个质心。一般建议使用默认的’k-means++’)
algorithm	有“auto”, “full” or “elkan”三种选择。“full"就是传统的K-Means算法， “elkan”是elkan K-Means算法。默认的"auto"则会根据数据值是否是稀疏的，来决定如何选择"full"和“elkan”。一般数据是稠密的，就是 “elkan”，否则就是"full”。一般来说建议直接用默认的"auto"

• 设定k = 3，初始质心为前三组数据

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd
data = pd.read_csv('wine.csv')
x = data.values[:, 0:13]
# plt.scatter(x[:,0],x[:,:1],c='red',marker = 'o')
estimator = KMeans(n_clusters = 3, init=x[0:3],n_init=1)
estimator.fit(x)

# 打标签
Label_pred = estimator.labels_

x0 = x[Label_pred == 0]
x1 = x[Label_pred == 1]
x2 = x[Label_pred == 2]

plt.scatter(x0[:,3],x0[:,12],c='blue',marker = 'o')
plt.scatter(x1[:,3],x1[:,12],c='green',marker = 'o')
plt.scatter(x2[:,3],x2[:,12],c='red',marker = 'o')
plt.show()

【4】 利用KMeans算法对“iris.csv”数据集的无标签数据分为3类，用三维图形可视化分类结果。

K-means可视化——三维散点图

• 代码

  import matplotlib.pyplot as plt
  from sklearn.cluster import KMeans
  from mpl_toolkits.mplot3d import Axes3D
  import pandas as pd
  iris = pd.read_csv('iris.csv')
  
  x = iris.iloc[:, 1:5]
  # plt.scatter(x[:,0],x[:,:1],c='red',marker = 'o')
  
  estimator = KMeans(n_clusters = 3)
  estimator.fit(x)
  
  # 打标签
  Label_pred = estimator.labels_
  
  x0 = x[Label_pred == 0]
  x1 = x[Label_pred == 1]
  x2 = x[Label_pred == 2]
  
  # 三维散点图
  fig = plt.figure()
  ax = fig.gca(projection='3d')
  
  ax.scatter(x0.iloc[:,0],x0.iloc[:,2],x0.iloc[:, 3],c='blue',marker = 'o')
  ax.scatter(x1.iloc[:,0],x1.iloc[:,2],x1.iloc[:, 3],c='green',marker = 'o')
  ax.scatter(x2.iloc[:,0],x2.iloc[:,2],x2.iloc[:, 3],c='red',marker = 'o')
  ax.set_xlabel(iris.columns[1]+"(cm)")
  ax.set_ylabel(iris.columns[3]+"(cm)")
  ax.set_zlabel(iris.columns[4]+"(cm)")
  plt.show()
  

• 得到三维散点图

【5】 利用KMeans算法对“iris.csv”数据集的无标签数据分为3类，任取2个特征值，显示分类结果

K-means可视化——多个子图

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
import numpy as np
iris = pd.read_csv('iris.csv')

x = iris.iloc[:, 1:5]
# plt.scatter(x[:,0],x[:,:1],c='red',marker = 'o')

estimator = KMeans(n_clusters = 3)
estimator.fit(x)

# 打标签
Label_pred = estimator.labels_

x0 = x[Label_pred == 0]
x1 = x[Label_pred == 1]
x2 = x[Label_pred == 2]

#划分子图
fig,axes=plt.subplots(4,4, sharex='col',figsize=(10, 10))
#plt.ylim(0,10)
for i in range(0,4):
    for j in range(0, 4):
        if i != j:
            axes[i, j].scatter(x0.iloc[:, j],x0.iloc[:, i],c='blue', marker='.')
            axes[i, j].scatter(x1.iloc[:, j], x1.iloc[:, i], c='red', marker='.')
            axes[i, j].scatter(x2.iloc[:, j],x2.iloc[:, i],c='green', marker='.')


    axes[i,i].hist(x.iloc[:,i], bins=20, facecolor="blue", edgecolor="black", alpha=0.7)
    
    axes[i, 0].set_ylabel(iris.columns[i+1]+"(cm)")
    axes[3, i].set_xlabel(iris.columns[i+1] + "(cm)")
#plt.tight_layout()

plt.show()

【6】你认为KMeans算法和KNN算法的缺陷是什么？针对这些缺点，通过查阅资料，了解到有什么改进的方法？

KMeans算法的缺陷及改进办法

(1) K-Means聚类算法需要用户事先指定聚类的个数k值.在很多时候,在对数据集进行聚类的时候,用户起初并不清楚数据集应该分为多少类合适,对k值难以估计.

改进方法—— 安徽大学李芳的硕士论文中提到了k-Means算法的k值自适应优化方法 ：可以通过在一开始给定一个适合的数值给k，通过一次K-means算法得到一次聚类中心。对于得到的聚类中心，根据得到的k个聚类的距离情况，合并距离最近的类，因此聚类中心数减小，当将其用于下次聚类时，相应的聚类数目也减小了，最终得到合适数目的聚类数。可以通过一个评判值E来确定聚类数得到一个合适的位置停下来，而不继续合并聚类中心。重复上述循环，直至评判函数收敛为止，最终得到较优聚类数的聚类结果。

*（2) **对初始聚类中心敏感,*选择不同的聚类中心会产生不同的聚类结果和不同的准确率.随机选取初始聚类中心的做法会导致算法的不稳定性,有可能陷入局部最优的情况.

改进方法—— K-Means++算法： 假设已经选取了n个初始聚类中心(0

(3) 对噪声和孤立点数据敏感,K-Means算法将簇的质心看成聚类中心加入到下一轮计算当中,因此少量的该类数据都能够对平均值产生极大影响,导致结果的不稳定甚至错误.

改进方法——离群点检测的LOF算法，通过去除离群点后再聚类，可以减少离群点和孤立点对于聚类效果的影响。

(4) 一旦集群具有复杂的几何形状，kmeans就不能很好地对数据进行聚类。

主要原因在于选取距离度量的方法。因为K-Means算法主要采用欧式距离函数度量数据对象之间的相似度,并且采用误差平方和作为准则函数,通常只能发现数据对象分布较均匀的球状簇.

改进方法：如果要处理不规则的数据，可以使用基于密度的DESCAN聚类算法。

• 参考文献

  《Kmeans聚类算法及其评价方法和改进方向的研究》 周银平　李卫国 （102206　华北电力大学　北京）

  https://blog.csdn.net/u013129109/article/details/80063111

  https://blog.csdn.net/u010536377/article/details/50884416

KNN算法的缺陷及改进方法

（1）需要更精确的距离函数代替欧氏距离

• 改进方法：
  • 消除不相关属性：缠绕法、贪婪搜索、遗传搜索
  • 属性加权距离函数
  • 基于频率的距离函数，称之为相异性度量
  • 标称属性的距离函数：值差分度量（VDM）

（2）搜索一个最优的近邻大小代替k

• 改进方法：
  • 交叉验证法
  • DKNN即动态确定K值

（3）找出更精确的类别概率估计代替简单的投票方法。

• 改进方法：

  • 基于概率的局部分类模型，即结合NB算法

作业清单（5/20）

【1】 数据集如下图所示，根据我们对决策树的理解，设计一棵决策树，并输入{Age:36,Salary:H,STU:No,Credit:OK} 测试数据，是否与预期结果一致？@注意，不允许直接调用Sklearn提供的决策树方法。

*Age*	*Salary*	*STU*	*Credit*	*Buy Computer*
<30	H	No	OK	No
<30	H	No	Good	No
30-40	H	No	OK	Yes
>40	M	No	OK	Yes
>40	L	Yes	OK	Yes
>40	L	Yes	Good	No
30-40	L	Yes	Good	Yes
<30	M	No	OK	No
<30	L	Yes	OK	Yes
>40	M	Yes	OK	Yes
<30	M	Yes	Good	Yes
30-40	M	No	Good	Yes
30-40	H	Yes	OK	Yes
>40	M	No	Good	No

• 决策树算法思想

  1. 使用信息增益选择最佳属性以拆分数据集。
  2. 使该属性成为决策节点，并将数据集分成较小的子集。
  3. 通过对每个子节点递归地重复此过程来开始树的构建，直到其中一个条件匹配：
     • 所有元组都属于相同的属性值。
     • 没有更多的剩余属性。
     • 没有更多实例了。

• 数据整理为csv格式

  Age,Salary,STU,Credit,BuyComputer
  <30,H,No,OK,No
  <30,H,No,Good,No
  30-40,H,No,OK,Yes
  >40,M,No,OK,Yes
  >40,L,Yes,OK,Yes
  >40,L,Yes,Good,No
  30-40,L,Yes,Good,Yes
  <30,M,No,OK,No
  <30,L,Yes,OK,Yes
  >40,M,Yes,OK,Yes
  <30,M,Yes,Good,Yes
  30-40,M,No,Good,Yes
  30-40,H,Yes,OK,Yes
  >40,M,No,Good,No
  

• 编码实现

  from math import log
  import pandas as pd
  # 计算信息熵
  def Ent(dataset):
      n = len(dataset)
      label_counts = {}
      for item in dataset:
          label_current = item[-1]
          if label_current not in label_counts.keys():
              label_counts[label_current] = 0
          label_counts[label_current] += 1
      ent = 0.0
      for key in label_counts:
          prob = label_counts[key]/n
          ent -= prob * log(prob,2)
      return ent
  
  #按照权重计算各分支的信息熵
  def sum_weight(grouped,total_len):
      
      weight = len(grouped)/total_len
      #print(grouped.iloc[:,-1])
      return weight * Ent(grouped.iloc[:,-1])
  
  #根据公式计算信息增益
  def Gain(column, data):
      lenth = len(data)
      ent_sum = data.groupby(column).apply(lambda x:sum_weight(x,lenth)).sum() 
      ent_D = Ent(data.iloc[:,-1])
      return ent_D - ent_sum
  
  # 计算获取最大的信息增益的feature，输入data是一个dataframe，返回是一个字符串
  def get_max_gain(data):
      max_gain = 0
      cols = data.columns[:-1]
      for col in cols:
          gain = Gain(col,data)
          if gain > max_gain:
              max_gain = gain
              max_label = col
      return max_label
  #获取data中最多的类别作为节点分类，输入一个series，返回一个索引值，为字符串
  def get_most_label(label_list):
      return label_list.value_counts().idxmax()
  
  # 创建决策树，传入的是一个dataframe，最后一列为label
  def TreeGenerate(data):
      feature = data.columns[:-1]
      label_list = data.iloc[:, -1]
      #如果样本全属于同一类别C，将此节点标记为C类叶节点
      if len(pd.unique(label_list)) == 1:
          return label_list.values[0]
      #如果待划分的属性集A为空，或者样本在属性A上取值相同，则把该节点作为叶节点，并标记为样本数最多的分类
      elif len(feature)==0 or len(data.loc[:,feature].drop_duplicates())==1:
          return get_most_label(label_list)
      #从A中选择最优划分属性
      best_attr = get_max_gain(data)
      tree = {best_attr: {}}
      #对于最优划分属性的每个属性值，生成一个分支
      for attr,gb_data in data.groupby(by=best_attr):
          print(gb_data)
          if len(gb_data) == 0:
              tree[best_attr][attr] = get_most_label(label_list)
          else:
              #在data中去掉已划分的属性
              new_data = gb_data.drop(best_attr,axis=1)
              #递归构造决策树
              tree[best_attr][attr] = TreeGenerate(new_data)
      return tree
  
  #使用递归函数进行分类
  def tree_predict(tree, data):
    feature = list(tree.keys())[0]
    label = data[feature]
    next_tree = tree[feature][label]
    if type(next_tree) == str:
      return next_tree
    else:
      return tree_predict(next_tree, data)
  
  data = pd.read_csv('computer.csv')
  
  #得到经过训练后的决策树
  mytree = TreeGenerate(data)
  print(mytree)
  test_data = {'Age':'30-40','Salary':'H','STU':'No','Credit':'OK'}
  predict = tree_predict(mytree,test_data)
  print(predict)
  

• 实验结果

  • 测试结果

    Yes

【2】数据集如下图所示，计算这棵决策树的类别信息熵，并计算基于每个特征值的类别信息熵。根据公式计算每个特征值的信息增益，画出一棵决策树（用签字笔画出即可）。

标签/特征值	类别特征值	信息增益
是否给贷款	-6/15 * log(6/15,2)-9/15 * log(9/15,2)=0.971
年龄	1/3 *(-2/5 * log(2/5,2) - 3/5 * log(3/5,2))+ 1/3 * (-2/5 * log(2/5,2) - 3/5 * log(3/5,2)) + 1/3 * (-1/5 * log(1/5,2)-4/5 * log(4/5,2)) = 0.888	0.971-0.888=0.083
有工作	1/3 * 0 + 2/3 * (-4/10 * log(4/10,2)-6/10 * log(6/10,2)) = 0.647	0.971-0.647=0.324
有自己的房子	6/15 * 0 + 9/15 * (- 3/9 * log(3/9,2)-6/9 * log(6/9,2)) = 0.551	0.971-0.551=0.420
信贷情况	5/15 * (-1/5 * log(1/5,2)-4/5 * log(4/5,2)) + 6/15 * (-2/6 * log(2/6,2)-4/6 * log(4/6,2)) + 4/15 * 0 = 0.608	0.971-0.608=0.363

【3】 根据下述数据集，编写代码实现信息熵、条件熵、信息增益等决策树的关键环节，并撰写实验报告。（最后一列是类别：是否提供贷款）

dataSet = [ [0, 0, 0, 0, ‘no’], #数据集

[0, 0, 0, 1, ‘no’],

[0, 1, 0, 1, ‘yes’],

​ [0, 1, 1, 0, ‘yes’],

​ [0, 0, 0, 0, ‘no’],

​ [1, 0, 0, 0, ‘no’],

​ [1, 0, 0, 1, ‘no’],

​ [1, 1, 1, 1, ‘yes’],

​ [1, 0, 1, 2, ‘yes’],

​ [1, 0, 1, 2, ‘yes’],

​ [2, 0, 1, 2, ‘yes’],

​ [2, 0, 1, 1, ‘yes’],

​ [2, 1, 0, 1, ‘yes’],

​ [2, 1, 0, 2, ‘yes’],

​ [2, 0, 0, 0, ‘no’]]

labels = [‘年龄’, ‘有工作’, ‘有自己的房子’, ‘信贷情况’]

实验报告

• 实验中使用的第三方库

  • math: 进行对数计算
  • pandas: 对数据进行整理划分

  from math import log
  import pandas as pd
  

• 计算信息熵

  • 公式
    $$Ihfo(D)=-\sum _{i=1}^m{p}_{i}lo{g}_2{p}_i$$

  def Ent(dataset):
      n = len(dataset)
      label_counts = {}
      for item in dataset:
          label_current = item
          if label_current not in label_counts.keys():
              label_counts[label_current] = 0
          label_counts[label_current] += 1
      ent = 0.0
      for key in label_counts:
          prob = label_counts[key]/n
          ent -= prob * log(prob,2)
      return ent
  

• 计算条件熵

  • 公式：
    $$Inf{o}_A(D)=\sum _{j=1}^v[(\frac{|D_j|}{|D|})\times Info(D_j)]$$

    #按照权重计算各分支的信息熵
    def sum_weight(grouped,total_len):
        
        weight = len(grouped)/total_len
        #print(grouped.iloc[:,-1])
        return weight * Ent(grouped.iloc[:,-1])
    

  • 计算条件熵时利用DataFrame.groupby,apply 进行分组

    # 计算条件熵
    ent_sum = data.groupby(column).apply(lambda x:sum_weight(x,lenth)).sum()
    

• 计算信息增益

  • 公式：
    $$Grain(D)=Info(D)-Inf{o}_A(D)$$

    #根据公式计算信息增益
    def Gain(column, data):
        lenth = len(data)
        ent_sum = data.groupby(column).apply(lambda x:sum_weight(x,lenth)).sum() 
        ent_D = Ent(data.iloc[:,-1])
        print(column,ent_D-ent_sum)
        return ent_D - ent_sum
    

• 递归生成决策树

  1. 使用信息增益选择最佳属性以拆分数据集。
  2. 使该属性成为决策节点，并将数据集分成较小的子集。
  3. 通过对每个子节点递归地重复此过程来开始树的构建，直到其中一个条件匹配：
     • 所有元组都属于相同的属性值。
     • 没有更多的剩余属性。
     • 没有更多实例了

  # 计算获取最大的信息增益的feature,输入data是一个dataframe,返回是一个字符串
  def get_max_gain(data):
      max_gain = 0
      cols = data.columns[:-1]
      for col in cols:
          gain = Gain(col,data)
          if gain > max_gain:
              max_gain = gain
              max_label = col
      return max_label
  #获取data中最多的类别作为节点分类,输入一个series,返回一个索引值,为字符串
  def get_most_label(label_list):
      return label_list.value_counts().idxmax()
  
  # 创建决策树,传入的是一个dataframe,最后一列为label
  def TreeGenerate(data):
      feature = data.columns[:-1]
      label_list = data.iloc[:, -1]
      #如果样本全属于同一类别C,将此节点标记为C类叶节点
      if len(pd.unique(label_list)) == 1:
          return label_list.values[0]
      #如果待划分的属性集A为空,或者样本在属性A上取值相同,则把该节点作为叶节点,并标记为样本数最多的分类
      elif len(feature)==0 or len(data.loc[:,feature].drop_duplicates())==1:
          return get_most_label(label_list)
      #从A中选择最优划分属性
      best_attr = get_max_gain(data)
      tree = {best_attr: {}}
      #对于最优划分属性的每个属性值,生成一个分支
      for attr,gb_data in data.groupby(by=best_attr):
          #print(gb_data)
          if len(gb_data) == 0:
              tree[best_attr][attr] = get_most_label(label_list)
          else:
              #在data中去掉已划分的属性
              new_data = gb_data.drop(best_attr,axis=1)
              #递归构造决策树
              tree[best_attr][attr] = TreeGenerate(new_data)
      return tree
  

• 输入数据，生成决策树

  dataSet=[[0,0,0,0,'no'],[0,0,0,1,'no'],[0,1,0,1,'yes'],[0,1,1,0,'yes'],[0,0,0,0,'no'],
  [1,0,0,0,'no'],[1,0,0,1,'no'],[1,1,1,1,'yes'],[1,0,1,2,'yes'],[1,0,1,2,'yes'],
  [2,0,1,2,'yes'],[2,0,1,1,'yes'],[2,1,0,1,'yes'],[2,1,0,2,'yes'],[2,0,0,0,'no']]
  
  labels = ['年龄', '有工作', '有自己的房子', '信贷情况','是否提供贷款']  
  
  data = pd.DataFrame(dataSet,columns=labels)
  tree = TreeGenerate(data)
  print(tree)
  

  • 结果以字典形式输出

    {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
    

【1】 对问题【3】中实现的决策树，实现可视化。（选做）

import matplotlib.pyplot as plt
#为了matplotlib中文正常显示，指定字体为SimHei
plt.rcParams['font.sans-serif']=['SimHei'] 
plt.rcParams['font.family']='sans-serif'

# 获取树的叶子节点数目
def get_num_leafs(decision_tree):
    num_leafs = 0
    first_str = next(iter(decision_tree))
    second_dict = decision_tree[first_str]
    for k in second_dict.keys():
        if isinstance(second_dict[k], dict):
            num_leafs += get_num_leafs(second_dict[k])
        else:
            num_leafs += 1
    return num_leafs

# 获取树的深度
def get_tree_depth(decision_tree):
    max_depth = 0
    first_str = next(iter(decision_tree))
    second_dict = decision_tree[first_str]
    for k in second_dict.keys():
        if isinstance(second_dict[k], dict):
            this_depth = 1 + get_tree_depth(second_dict[k])
        else:
            this_depth = 1
        if this_depth > max_depth:
            max_depth = this_depth
    return max_depth

# 绘制节点
def plot_node(node_txt, center_pt, parent_pt, node_type):
    arrow_args = dict(arrowstyle='<-')
    create_plot.ax1.annotate(node_txt, xy=parent_pt,  xycoords='axes fraction', xytext=center_pt, textcoords='axes fraction', va="center", ha="center", bbox=node_type,arrowprops=arrow_args)

# 标注划分属性
def plot_mid_text(cntr_pt, parent_pt, txt_str):
    x_mid = (parent_pt[0] - cntr_pt[0]) / 2.0 + cntr_pt[0]
    y_mid = (parent_pt[1] - cntr_pt[1]) / 2.0 + cntr_pt[1]
    create_plot.ax1.text(x_mid, y_mid, txt_str, va="center", ha="center", color='red')

# 绘制决策树
def plot_tree(decision_tree, parent_pt, node_txt):
    d_node = dict(boxstyle="sawtooth", fc="0.8")
    leaf_node = dict(boxstyle="round4", fc='0.8')
    num_leafs = get_num_leafs(decision_tree)
    first_str = next(iter(decision_tree))
    cntr_pt = (plot_tree.xoff + (1.0 +float(num_leafs))/2.0/plot_tree.totalW, plot_tree.yoff)
    plot_mid_text(cntr_pt, parent_pt, node_txt)
    plot_node(first_str, cntr_pt, parent_pt, d_node)
    second_dict = decision_tree[first_str]
    plot_tree.yoff = plot_tree.yoff - 1.0/plot_tree.totalD
    for k in second_dict.keys():
        if isinstance(second_dict[k], dict):
            plot_tree(second_dict[k], cntr_pt, k)
        else:
            plot_tree.xoff = plot_tree.xoff + 1.0/plot_tree.totalW
            plot_node(second_dict[k], (plot_tree.xoff, plot_tree.yoff), cntr_pt, leaf_node)
            plot_mid_text((plot_tree.xoff, plot_tree.yoff), cntr_pt, k)
    plot_tree.yoff = plot_tree.yoff + 1.0/plot_tree.totalD

def create_plot(dtree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    create_plot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plot_tree.totalW = float(get_num_leafs(dtree))
    plot_tree.totalD = float(get_tree_depth(dtree))
    plot_tree.xoff = -0.5/plot_tree.totalW
    plot_tree.yoff = 1.0
    plot_tree(dtree, (0.5, 1.0), '')
    plt.show()

tree = {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}

create_plot(tree)

• 参考资料：https://zhuanlan.zhihu.com/p/43819989

作业清单（5/27）

【1】在下列事务数据集中

TID	项集
1	{面包,牛奶}
2	{面包,尿布,啤酒,鸡蛋}
3	{牛奶,尿布,啤酒,可乐}
4	{面包,牛奶,尿布,啤酒}
5	{面包,牛奶,尿布,可乐}

• 项集{啤酒，尿布，牛奶}的支持度为 2/5=40%

• 如果将最小支持度定为3，则数据集中的频繁项集有

  L1

频繁项集	支持度
{面包}	4
{啤酒}	3
{牛奶}	4
{尿布}	4

​ L2

频繁项集	支持度
{面包，牛奶}	3
{面包，尿布}	3
{啤酒，尿布}	3
{牛奶，尿布}	3

• 规则{牛奶，尿布}→{啤酒}的支持度为 2/5=40% ，置信度为 2/3=66.7% 。

【2】阅读微信群发布的“关联规则例子.py”，并根据交易单为（T1，T2，T3，T4，T5，T6，T7，T8，T9），每笔交易的货物清单为{{I1，I2，I5},{I2，I4},{I2，I3},{I1，I2，I4},{I1，I3},{I2，I3},{I1，I3},{I1，I2，I3，I5},{I1，I2，I3}}，编写代码得到关联规则。

A strong rule is a rule that is frequent and its confidence is higher than Minimum confidence Φ

• 模型搭建

  • 模型初始化及参数设置（最小支持度=0.1，最小置信度=0.5）

  def __init__(self,minSupport=0.1,minConfidence=0.5):
  		'''
  		minSuport:最小支持度
  		minConfidence:最小置信度
  		dataset:数据集
  		count:存放frequent itemsets 以及 support
  		associationRules:满足minConfidence的关联规则
  		num:元素数量
  		threshold = num*minSupport：由num和minSupport算出的阈值
  		'''
  		self.minSupport = minSupport
  		self.minConfidence = minConfidence
  		self.dataset = None
  		self.count = None
  		self.associationRules = None
  		self.num = 0
  		self.threshold = 0
  

  • 生成频繁项集

    思路：

    1. 先遍历数据集，统计元素数量num，得到候选集C1；

    2. 由num*minSupport得到阈值threhold；

    3. 去掉支持度小于threhold的项集，得到size=1的频繁项集L1；

    4. 将上一步得到的频繁项集两两合并，得到新的候选集；

    5. 去掉支持度小于threhold的项集，得到新的频繁项集；

    6. 循环4~5，直至找到所有频繁项集.

    修改微信群发布的“关联规则例子.py”：

    1.  原例子中对元素数量的计算有误，作业中进行了修正
    2.  修改微信群发布的“关联规则例子.py”，避免项集集合化数据项不会被拆分
    

    • 原例子

      tmp = set(list(element[i]))
      tmp.update(list(element[j]))
      

      [‘I1’]和[‘I2’]合并为[‘I’,‘1’,‘2’]

    • 修改为

      tmp = set([element[i],element[j]])
      

      [‘I1’]和[‘I2’]合并为[‘I1’,‘I2’]

    class Association_rules:
        #计算frequent itemset
    	def countItem(self,upDict,elength):
    		currentDict = {}
    		element = list(upDict.keys())
    		for i in range(len(element)-1):
    			for j in range(i+1,len(element)):
    				#print(element[i])
    				tmp = set([element[i],element[j]])
    				#tmp.update(list(element[j]))
    				#print(tmp)
    
    				if len(tmp) > elength:
    					continue
    				if tmp in list(set(item) for item in currentDict.keys()):
    					continue
    
    				
    				for item in self.dataset:
    					if tmp.issubset(set(item)):
    						if tmp in list(set(item) for item in currentDict.keys()):
    							currentDict[tuple(tmp)] += 1
    						else:
    							currentDict[tuple(tmp)] = 1
    
    		for item in list(currentDict.keys()):
    			if currentDict[item] < self.threshold:
    				del currentDict[item]
    		if len(list(currentDict.keys())) < 1:
    			return None
    		else:
    			return currentDict
     
    	#生成frequent itemsets
    	def fit(self,dataset):
    		self.dataset = dataset
    		count = []
    		count.append({})
    		for item in self.dataset:
    			for i in range(len(item)):
    				if item[i] in list(count[0].keys()):
    					count[0][item[i]] += 1
    				else:
    					count[0][item[i]] = 1
    				self.num += 1
     
    		self.threshold = self.num * self.minSupport
    		print(self.num, self.threshold)
    		for item in list(count[0].keys()):
    			if count[0][item] < self.threshold:
    				del count[0][item]
    		
    			
    		i = 0
    		while(True):
    			if len(count[i]) < 2:
    				break
    			else:
    				tmp = self.countItem(count[i],i+2)
    				if tmp == None:
    					break
    				else:
    					count.append(tmp)
    				i += 1
    
    
    		self.count = count
     
    	#打印并返回frequent itemsets
    	def frequentItemsets(self):
    		#print('threshold:',self.threshold)
    		for item in self.count:
    			print(item)
    			print()
    		return self.count
    

  • 计算置信度

    公式：
    $$Confidence(X=>Y)=\frac{|X，Y|}{|X-Items|}$$

    class Association_rules:
        #计算置信度。set = (X),set2 = (X^Y)
    	def countConfidence(self,set1,set2):
    		len1 = len(set1)
    		len2 = len(set2)
    		#去除元素位置干扰。例如：set2 = ('a','b'),而self.count中存储为('b','a')
    		if not tuple(set2) in self.count[len2-1].keys():
    			set2[0],set[1] = set2[1],set2[0]
    		#写代码的时候出现的疏忽，当元素只有一个时count中存储格式是str，而元素多于一个时格式是tuple
    		if len1 == 1:
    			return self.count[len2-1][tuple(set2)] / self.count[len1-1][set1[0]]
    		else:
    			if not tuple(set1) in self.count[len1-1].keys():
    				set1[0],set1[1] = set1[1],set1[0]
    			return self.count[len2-1][tuple(set2)] / self.count[len1-1][tuple(set1)] 
    

  • 二进制求子集

    算法思想：

    ​ 例如求4个元素 3 2 1 0 的子集，那么用二进制的0，1代表每一位是否选中。
    十进制 二进制
    0 0000 代表空集
    1 0001 代表{0}
    2 0010 代表{1}
    3 0011 代表{0,1}
    4 0100 代表{2}
    ​ …
    15 1110 代表{3,2,1}
    16 1111 代表{3,2,1,0}

    	#二进制法求每个itemset的所有子集
    	def subsets(self,itemset):
    		N = len(itemset)
    		subsets = []
    		for i in range(1,2**N-1):
    			tmp = []
    			for j in range(N):
    				if (i >> j) % 2 == 1:
    					tmp.append(itemset[j])
    			subsets.append(tmp)
    		return subsets
    

  • 生成关联规则

    • 判断频繁项集中的每个规则的置信度是否大于最小置信度

    	def associationRule(self):
    		associationRules = []
    		for i in range(1,len(self.count)):
    			for itemset in list(self.count[i].keys()):
    				#用字典存每个itemset的关联规则
    				tmp = {}
    				#print(itemset)
    				subset = self.subsets(itemset)
    				#print(subset)
    				for i in range(len(subset)-1):
    					for j in range(i+1,len(subset)):
    						#判断subset[i]与subset[j]完整组成一个itemset，而且没有相同的元素
    						if len(subset[i]) + len(subset[j]) == len(itemset) and len(set(subset[i]) & set(subset[j])) == 0:
    							confidence = self.countConfidence(subset[i],itemset)
    							#print(subset[i],' > ',subset[j],' ',confidence)
    							if confidence > self.minConfidence:
    								#生成相应键值对
    								tmpstr = str(subset[i]) + ' > ' + str(subset[j])
    								tmp[tmpstr] = confidence
    							#将subset[i]与subset[j]反过来生成另外一个规则
    							confidence = self.countConfidence(subset[j],itemset)
    							#print(subset[j],' > ',subset[i],' ',confidence)
    							if confidence > self.minConfidence:
    								tmpstr = str(subset[j]) + ' > ' + str(subset[i])
    								tmp[tmpstr] = confidence
    				if tmp.keys():
    					associationRules.append(tmp)
    		for item in associationRules:
    			print(item)
    		return associationRules
    

  2. 调用模型，得出结果

     if __name__ == '__main__':
     	num = 10
     	#dataset = set_data(num)
     	dataset = [['I1','I2','I5'],['I2','I4'],['I2','I3'],
     	['I1','I2','I4'],['I1','I3'],['I2','I3'],['I1','I3'],['I1','I2','I3','I5'],['I1','I2','I3']]
     	for item in dataset:
     		print(item)
     
     	ar = Association_rules()
     	ar.fit(dataset)
     	freItemsets = ar.frequentItemsets()
     	associationRules = ar.associationRule()
     

     得到关联规则

     关联规则	支持度	置信度
     {I1} --> {I2}	4	0.67
     {I2} --> {I1}	4	0.57
     {I1} --> {I3}	4	0.67
     {I3} --> {I1}	4	0.67
     {I3} --> {I2}	4	0.67
     {I2} --> {I3}	4	0.57

​ 例如求4个元素 3 2 1 0 的子集，那么用二进制的0，1代表每一位是否选中。
十进制 二进制
0 0000 代表空集
1 0001 代表{0}
2 0010 代表{1}
3 0011 代表{0,1}
4 0100 代表{2}
​ …
15 1110 代表{3,2,1}
16 1111 代表{3,2,1,0}

```python
	#二进制法求每个itemset的所有子集
	def subsets(self,itemset):
		N = len(itemset)
		subsets = []
		for i in range(1,2**N-1):
			tmp = []
			for j in range(N):
				if (i >> j) % 2 == 1:
					tmp.append(itemset[j])
			subsets.append(tmp)
		return subsets
```

• 生成关联规则

  • 判断频繁项集中的每个规则的置信度是否大于最小置信度

  	def associationRule(self):
  		associationRules = []
  		for i in range(1,len(self.count)):
  			for itemset in list(self.count[i].keys()):
  				#用字典存每个itemset的关联规则
  				tmp = {}
  				#print(itemset)
  				subset = self.subsets(itemset)
  				#print(subset)
  				for i in range(len(subset)-1):
  					for j in range(i+1,len(subset)):
  						#判断subset[i]与subset[j]完整组成一个itemset，而且没有相同的元素
  						if len(subset[i]) + len(subset[j]) == len(itemset) and len(set(subset[i]) & set(subset[j])) == 0:
  							confidence = self.countConfidence(subset[i],itemset)
  							#print(subset[i],' > ',subset[j],' ',confidence)
  							if confidence > self.minConfidence:
  								#生成相应键值对
  								tmpstr = str(subset[i]) + ' > ' + str(subset[j])
  								tmp[tmpstr] = confidence
  							#将subset[i]与subset[j]反过来生成另外一个规则
  							confidence = self.countConfidence(subset[j],itemset)
  							#print(subset[j],' > ',subset[i],' ',confidence)
  							if confidence > self.minConfidence:
  								tmpstr = str(subset[j]) + ' > ' + str(subset[i])
  								tmp[tmpstr] = confidence
  				if tmp.keys():
  					associationRules.append(tmp)
  		for item in associationRules:
  			print(item)
  		return associationRules
  

2. 调用模型，得出结果

   if __name__ == '__main__':
   	num = 10
   	#dataset = set_data(num)
   	dataset = [['I1','I2','I5'],['I2','I4'],['I2','I3'],
   	['I1','I2','I4'],['I1','I3'],['I2','I3'],['I1','I3'],['I1','I2','I3','I5'],['I1','I2','I3']]
   	for item in dataset:
   		print(item)
   
   	ar = Association_rules()
   	ar.fit(dataset)
   	freItemsets = ar.frequentItemsets()
   	associationRules = ar.associationRule()
   

   得到关联规则

   关联规则	支持度	置信度
   {I1} --> {I2}	4	0.67
   {I2} --> {I1}	4	0.57
   {I1} --> {I3}	4	0.67
   {I3} --> {I1}	4	0.67
   {I3} --> {I2}	4	0.67
   {I2} --> {I3}	4	0.57